Общее резервирование с замещением с целой кратностью

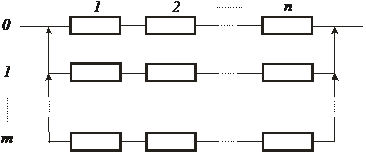
Рис.3. Общее резервирование замещением с целой кратностью

При ненагруженном резервировании вероятность безотказной работы резервированной системы определяется по формуле:

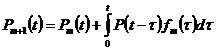, (17)

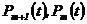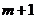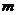где – вероятности безотказной работы резервированной системы кратности и соответственно; 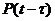– вероятность безотказной работы основной системы в течение времени 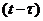; 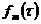– частота отказов резервной системы кратности 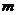в момент времени .

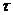Рекуррентная формула (17) позволяет получить расчетные соотношения для устройств любой кратности резервирования. Для получения таких формул необходимо выполнить интегрирование в правой части, подставив вместо 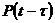и 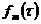их значения в соответствии с выбранным законом распределения и состоянием резерва.

При экспоненциальном законе надежности, ненагруженном состоянии резерва и равнонадежных элементах вероятность безотказной работы и средняя наработка до первого отказа резервированной системы определяются по формулам (18, 19):

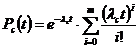, (18)

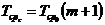, (19)

где 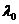и 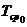– интенсивность отказов и средняя наработка до первого отказа основного (нерезервированного) устройства.

При экспоненциальном законе и недогруженном состоянии резерва

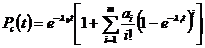, (20)

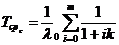, (21)

где 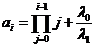, , 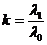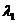– интенсивность отказов резервного устройства до замещения.

4. Раздельное резервирование замещением с целой кратностью.При раздельном резервировании, как уже отмечалось выше, резервируются отдельные элементы или группы элементов. Надежностная схема раздельного резервирования замещением с целой кратностью приведена на рис. 5.8.

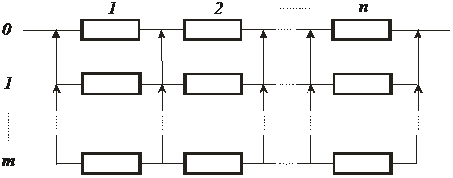
Рис.4. Раздельное резервирование замещением с целой кратностью

Вероятность безотказной работы резервированной системы определяется по формуле:

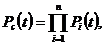(22)

где 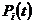– вероятность безотказной работы системы из-за отказов элементов i-го типа, резервированных по способу замещения. 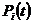вычисляется по формулам общего резервирования замещением (18), (19), (20).

5. Общее резервирование с дробной кратностью и постоянно включенным резервом.Метод резервирования, при котором отношение числа запасных элементов к числу основных не является целым числом, является резервированием с дробной кратностью (рис. 5).

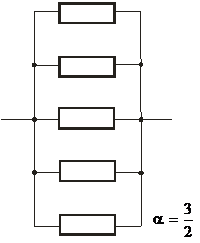
Рис. 5. Общее резервирование с дробной кратностью и постоянно включенным резервом (кратность резервирования 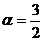, т.е число резервных элементов равно трем, число основных – двум).

При общем резервировании с дробной кратностью и постоянно включенным резервом вероятность безотказной работы определяется формулой

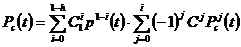, (23)

Средняя наработка до первого отказа системы резервированной системы равна

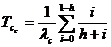, (24)

где 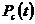– вероятность безотказной работы основного или любого резервного элемента; 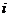– общее число основных и резервных систем; 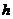– число систем, необходимых для нормальной работы.

В данном случае кратность резервирования

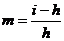. (25)

Приведенные выше формулы [кроме выражений (19), (22), (23)] могут быть использованы только в тех случаях, когда справедливо допущение об отсутствии последействия отказов. Последействие отказов имеет место практически всегда при постоянном включении резерва, а также в случае резервирования замещением при недогруженном состоянии резерва. Выражение (19) является основным при получении расчетных формул в случае учета влияния последействия отказов, при этом члены 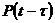и 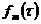должны быть вписаны с учетом последействия отказов, вида резервирования и его кратности.

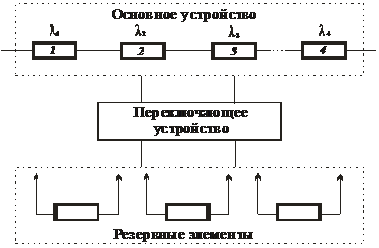6. Скользящее резервирование.Для резервирования объектов, состоящих из одинаковых элементов, можно использовать сравнительно небольшое число резервных элементов, которые подключаются взамен любых отказавших основных. Отказ системы наступает лишь в случае, когда число отказавших основных элементов превысит число резервных. Такое резервирование называется скользящим из-за того, что резервный элемент может быть включен взамен любого из элементов основной системы. Так как число резервных элементов обычно меньше числа основных, этот вид резервирования можно назвать также разновидностью резервирования с дробной кратностью [12]. Примером скользящего резервирования может служить одна резервная линия связи на три основные. При скользящем резервировании всегда имеется переключающее устройство, определяющее наличие отказа и включающее резервный элемент (рис. 6).

Рис. 6. Схема скользящего резервирования

Формулы для расчета надежности системы со скользящим резервированием можно получить, выделив возможные состояния системы, при которых она продолжает безотказно работать, и вычислив вероятности этих состояний. В качестве примера выведем формулу для случая, когда применяется один резервный элемент (ненагруженное резервирование) и n работающих элементов основной системы.

Пусть резервный элемент и все элементы основной системы равнонадежны и применяется ненагруженный резерв, т.е. резервный элемент не может отказать до момента его включения в работу. Рассматриваемая система будет безотказно работать в течение наработки (0, t) при следующих несовместных событиях:

1) все элементы основной системы работают безотказно;

2) отказал один элемент из общего числа n+1 основных и резервных элементов в системе, причем переключающее устройство работоспособно.

Вероятность первого из этих событий равна

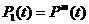, (26)

где 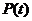– вероятность безотказной работы одного элемента.

Чтобы вычислить вероятность второго события, рассмотрим малый интервал 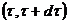,лежащий внутри периода (0, t). Выделим один элемент основной системы (например, первый) и рассмотрим его работу на интервале 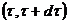. Вероятность появления отказа этого элемента в течение наработки 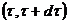равна 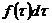. Вероятность того, что в течение наработки 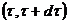система не откажет из-за рассматриваемого элемента, равна

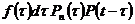, (27)

где 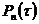– вероятность безотказной работы переключаю­щего устройства до наработки t; 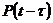– вероятность безотказной работы резервного элемента, начиная с момента t его включения.

Интегрируя по всем t от 0 до t, получим вероятность того, что в течение наработки 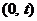система не откажет из-за рассматриваемого элемента будет равна:

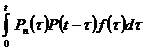. (28)

Учитывая, что такие рассуждения можно провести для каждого из n элементов основной системы и что после отказа одного из элементов основной системы 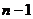элементов должны остаться работоспособными, получим выражение для вероятности второго из указанных выше двух не­совместных событий:

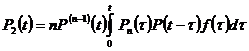. (29)

Вероятность безотказной работы рассматриваемой системы со скользящим резервом

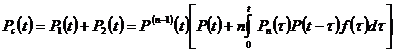. (30)

При показательном распределении времени до отказа основных и резервного элементов и переключающего устройства согласно (30) вероятность безотказной работы системы будет определяться формулой:

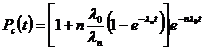, (31)

где 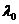– интенсивность отказов работающего (основного или резервного) элемента; 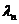– интенсивность отказов переключающего устройства.

В случае абсолютно надежного переключателя формулы (30 и 31) можно переписать следующим образом:

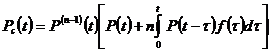. (32)

При показательном распределении наработки до отказа устройства:

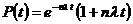. (33)

При двух резервных элементах рассматриваются четыре несовместных события, при которых возможна безотказная работа системы, и т.д.

В этом случае вероятность безотказной работы системы со скользящим резервом определяется выражением:

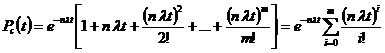. (34)

Далее приведены примеры решения задач на повышение надежности систем путем резервирования.