Тема 2. дифференциальное исчисление функции одной переменной
1.Сформулируйте определение производной. Каков геометрический смысл производной?
2.Функция имеет производную в данной точке. Следует ли отсюда, что она непрерывна в этой точке?
3.В чем заключается правило Лопиталя? При каких условиях применяется правило Лопиталя? Перечислите различные типы неопределённостей, для раскрытия которых может быть использовано это правило. Приведите примеры.
4.Что называется дифференциалом функции? Приведите примеры.
5.Каковы признак» возрастания и убывания функции?
6.Что такое экстремум функции? Каковы необходимые и достаточные условия экстремума? Приведите примеры.
7.Приведите пример, показывающий, что обращение производнойв нуль не является достаточным условием экстремума.
8.Как найти интервалы выпуклости и точки перегиба графика функции? Приведите примеры.
9.Что называется дифференциалом функции? Как он применяется при приближенных вычислениях?
ТЕМА 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
1.Сформулируйте определение первообразной функции. Докажите, что любые две первообразные одной и той же функции отличаются на константу.
2.Что называется неопределённым интегралом?
3.Какие правила применяются для вычисления неопределённого интеграла суммы функций, для вычисления 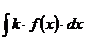 ?
?
4.Как выглядит формула интегрирования по частям?
5.Какая фигура называется криволинейной трапецией? По какой формуле вычисляется её площадь?
6.Напишите формулу Ньютона-Лейбница.
7.Какие свойства определённого интеграла Вам известны?
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Основная литература:
1.Щипачев В.С. Математический анализ. Теория и практика: Учебное пособие / В.С. Шипачев. - 3-e изд. - М.: НИЦ ИНФРА-М, 2015. - 351 с. (Высшее образование).
2.Шершнев В.Г.Математический анализ: Учебное пособие / В.Г. Шершнев. – М.: НИЦ ИНФРА-М, 2014. - 288 с. (Высшее образование: Бакалавриат).
Дополнительная литература:
1.Высшая математика для экономистов: Учебное пособие / О.А. Кастрица, 4-е изд., стер. - М.: НИЦ ИНФРА-М, Нов. знание, 2015. - 491 с. - (Высшее образование: Бакалавриат)
2.Задачник по высшей математике: Учебное пособие / В.С. Шипачев. – 10-e изд., стер. - М.: НИЦ ИНФРА-М, 2015. - 304 с. - (Высшее образование).
3.Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер и др. – 2-е изд., перераб. и доп. – М.: Юнити, 2002. – 471 с.
КОНТРОЛЬНАЯ РАБОТА № 1
Формулировки условий задач контрольной работы:
1.Вычислить пределы функций.
2.Исследовать на непрерывность функции и построить схематично их график.
3.Вычислить производные функций.
4.Исследовать функцию, построить график.
5.Вычислить неопределённые интегралы.
6.Вычислить определенный интеграл.
7.Вычислить площадь фигуры, ограниченной графиками функций f(x) и 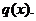
►Вариант 0◄
1.а) 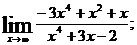 б)
б) 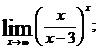
в) 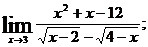 г)
г) 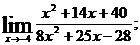
2.а) 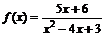 ; б)
; б) 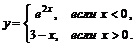
3.а) 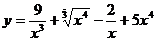 ; б)
; б) 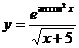 ; в)
; в) 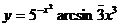
4. 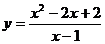 .
.
5.а) 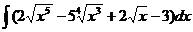 ; б)
; б) 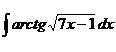
6. 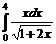
7. 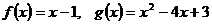 .
.
►Вариант 1◄
1.а) 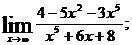 б)
б) 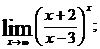
в) 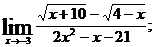 г)
г) 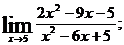
2.а) 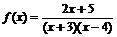 ; б)
; б) 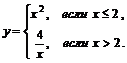
3.а) 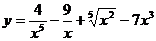 ; б)
; б) 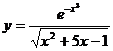 ; в)
; в) 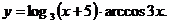
4. 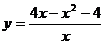 .
.
5.а) 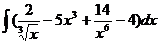 б)
б) 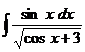
6. 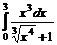
7. 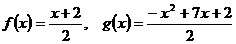 .
.
►Вариант 2◄
1.а) 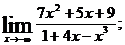 б)
б) 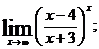
в) 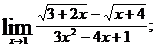 г)
г) 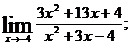
2.а) 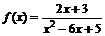 ; б)
; б) 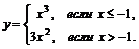
3.а) 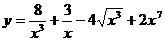 ; б)
; б) 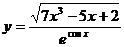 ; в)
; в) 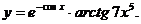
4. 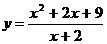
5.а) 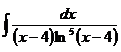 ; б)
; б) 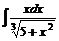
6. 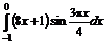
7. 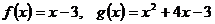 .
.
►Вариант 3◄
1.а) 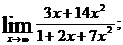 б)
б) 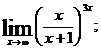
в) 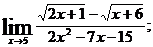 г)
г) 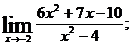
2.а) 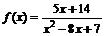 ; б)
; б) 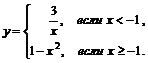
3.а) 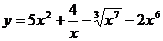 ; б)
; б) 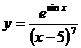 ; в)
; в) 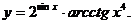
4. 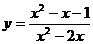 .
.
5.а) 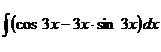 ; б)
; б) 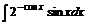
6. 
7. 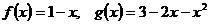 .
.
►Вариант 4◄
1.а) 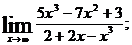 б)
б) 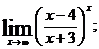
в) 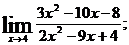 г)
г) 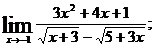
2.а) 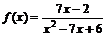 ; б)
; б) 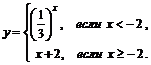
3.а) 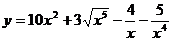 ; б)
; б) 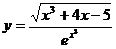 ; в)
; в) 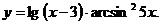
4. 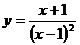
5.а) 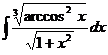 ; б)
; б) 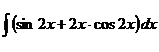 ;
;
6. 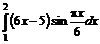
7. 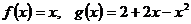
►Вариант 5◄
1.а) 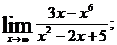 б)
б) 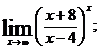
в) 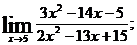 г)
г) 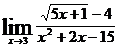
2.а) 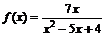 ; б)
; б) 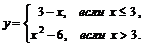
3.а) 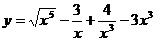 ; б)
; б) 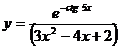 ; в)
; в) 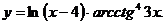
4. 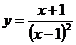
5.а) 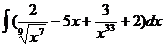 ; б)
; б) 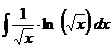
6. 
7. 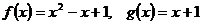 .
.
►Вариант 6◄
1.а) 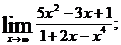 б)
б) 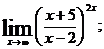
в) 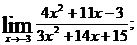 г)
г) 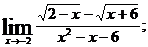
2.а) 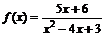 ; б)
; б) 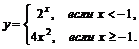
3.а) 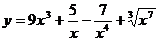 ; б)
; б) 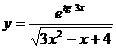 ; в)
; в) 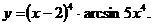
4. 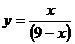
5.а) 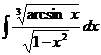 ; б)
; б) 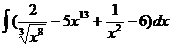
6.. 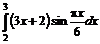
7. 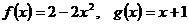
►Вариант 7◄
1. а) 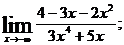 б)
б) 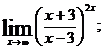
в) 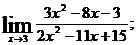 г)
г) 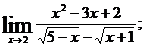
2.а) 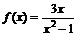 ; б)
; б) 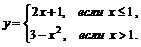
3.а) 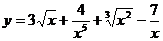 ; б)
; б) 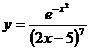 ; в)
; в) 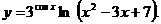
4. 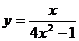
5.а) 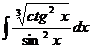 ; б)
; б) 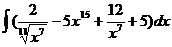
6. 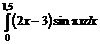
7. 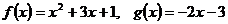 .
.
►Вариант 8◄
1. а) 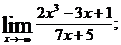 б)
б) 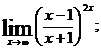
в) 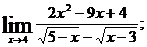 г)
г) 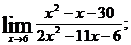
2.а) 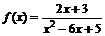 ; б)
; б) 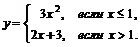
3.а) 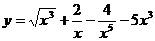 ; б)
; б) 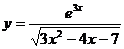 ; в)
; в) 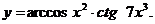
4. 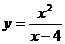
5.а) 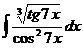 ; б)
; б) 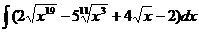
6. 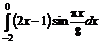
7. 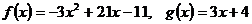
►Вариант 9◄
1. а) 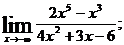 б)
б) 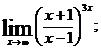
в) 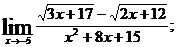 г)
г) 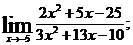
2.а) 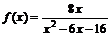 ; б)
; б) 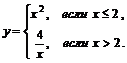
3.а)  ; б)
; б) 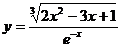 ; в)
; в) 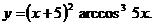
4. 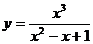
5.а) 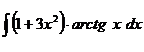 ; б)
; б) 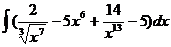
6. 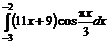
7. 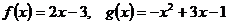
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ПЕРВОЙ КОНТРОЛЬНОЙ РАБОТЫ (примеры решений)
ЗАДАЧА 1. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЙ
Чтобы вычислить предел функции в точке, нужно:
1) Подставить вместо переменной x то число, к которому x стремится.
2) Если после выполнения пункта 1) получим неопределенность вида 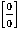 , то нужно числитель и знаменатель дроби разложить на множители и сократить дробь, или числитель и знаменатель домножить на сопряженное и после этого сократить дробь.
, то нужно числитель и знаменатель дроби разложить на множители и сократить дробь, или числитель и знаменатель домножить на сопряженное и после этого сократить дробь.
3) Если после выполнения пункта 1) получим неопределенность вида  , то нужно числитель и знаменатель дроби разделить на старшую степень неизвестного, или слагаемое с самой большой степенью в числителе разделить на слагаемое с самой большой степенью в знаменателе и взять предел от результата деления.
, то нужно числитель и знаменатель дроби разделить на старшую степень неизвестного, или слагаемое с самой большой степенью в числителе разделить на слагаемое с самой большой степенью в знаменателе и взять предел от результата деления.
4) Если после выполнения пункта 1) получилась неопределенность вида 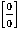 , связанная со значениями тригонометрических функций, необходимо воспользоваться первым замечательным пределом:
, связанная со значениями тригонометрических функций, необходимо воспользоваться первым замечательным пределом:
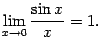
5) Второйзамечательный предел:
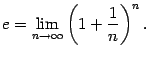
Пример 1
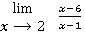 =
= 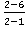 = -4
= -4
Мы воспользовались правилом 1) и подставили вместо x то, к чему x стремиться, т.е. x=2.
Пример 2
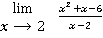 =
= 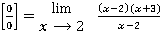 =
= 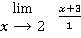 =
= 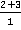 =5
=5
В этом примере мы разложили числитель на множители и сократили числитель и знаменатель на одинаковый множитель.
Пример 3
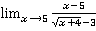 =
= 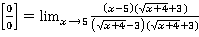 =
= 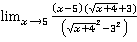 =
= 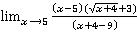 =
= 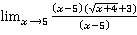 =
= 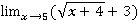 =3+3=6
=3+3=6
В этом примере числитель и знаменатель умножили на сопряженное выражение знаменателю.
Пример 4
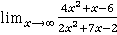 =
= 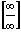 =
= 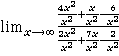 =
= 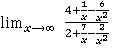 =
= 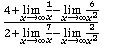 =
= 
Здесь и числитель, и знаменатель разделили на старшую степень х для всего выражения.
Пример 5
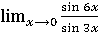 =
= 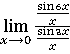 =
= 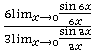 =
=  =2
=2
Домножили и числитель, и знаменатель на одинаковый множитель 1/х (значение выражения под знаком предела при этом не изменилось), затем для того, чтобы свести пример к первому замечательному пределу, домножили и разделили на необходимые множители числитель и знаменатель.
Пример 6
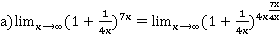 =
= 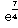
б) 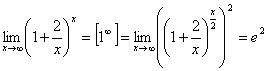
в) 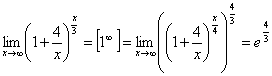
г) 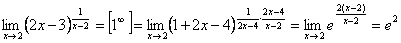
ЗАДАЧА 2.ИССЛЕДОВАНИЕ ФУНКЦИИ НА НЕПРЕРЫВНОСТЬ
а) 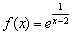 . Исследуем на непрерывность точку
. Исследуем на непрерывность точку 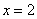
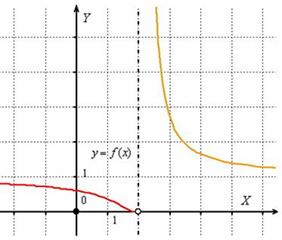
1) Функция не определена в данной точке.
2) Вычислим односторонние пределы:
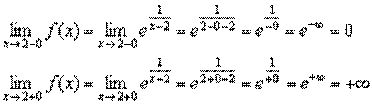
Левосторонний предел конечен и равен нулю (в саму точку мы «не заходим»), но правосторонний предел бесконечен и оранжевая ветка графика бесконечно близко приближается к своей вертикальной асимптоте, заданной уравнением 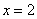 (чёрный пунктир).
(чёрный пунктир).
Таким образом, функция 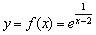 терпит разрыв второго рода в точке
терпит разрыв второго рода в точке 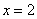
б) Исследовать функцию 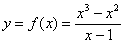 на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение:
1) Под прицел попадает единственная точка 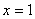 , в которой функция не определена.
, в которой функция не определена.
2) Вычислим односторонние пределы:
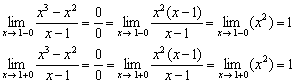
Односторонние пределы конечны и равны.
Таким образом, в точке 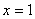 функция терпит устранимый разрыв.
функция терпит устранимый разрыв.
Как выглядит график данной функции?
Хочется провести упрощение 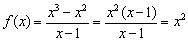 , и вроде бы получается обычная парабола.
, и вроде бы получается обычная парабола.
НО исходная функция не определена в точке 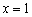 , поэтому обязательна следующая оговорка:
, поэтому обязательна следующая оговорка: 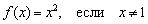
Выполним чертёж: 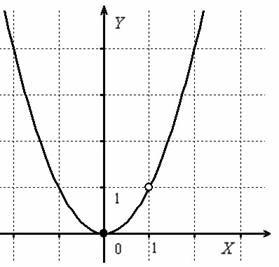
Ответ: функция непрерывна на всей числовой прямой кроме точки 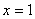 , в которой она терпит устранимый разрыв.
, в которой она терпит устранимый разрыв.
в) Исследовать функцию на непрерывность и построить график функции  .
.
Решение: очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому осталось проверить только две точки «стыка» между кусками. Сначала выполним чертёж на черновике, технику построения я достаточно подробно закомментировал в первой части статьи. Единственное, необходимо аккуратно проследить за нашими особенными точками: в силу неравенства 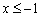 значение
значение 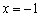 принадлежит прямой
принадлежит прямой 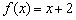 (зелёная точка), и в силу неравенство
(зелёная точка), и в силу неравенство 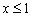 значение
значение 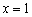 принадлежит параболе
принадлежит параболе 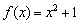 (красная точка):
(красная точка):
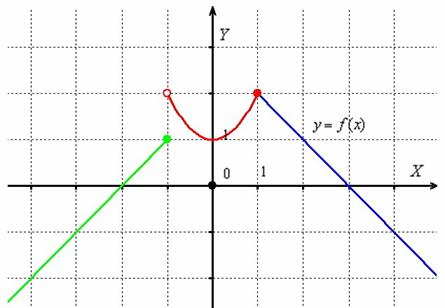
Для каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:
I) Исследуем на непрерывность точку 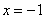
1) 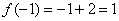 – функция определена в данной точке.
– функция определена в данной точке.
2) Найдём односторонние пределы:
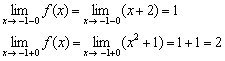
Односторонние пределы конечны и различны, значит, функция 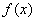 терпит разрыв 1-го рода со скачком в точке
терпит разрыв 1-го рода со скачком в точке 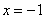 .
.
Вычислим скачок разрыва как разность правого и левого пределов:
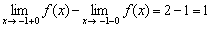 , то есть, график рванул на одну единицу вверх.
, то есть, график рванул на одну единицу вверх.
II) Исследуем на непрерывность точку 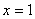
1) 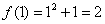 – функция определена в данной точке.
– функция определена в данной точке.
2) Найдём односторонние пределы:
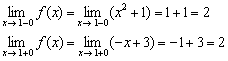
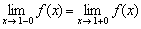 – односторонние пределы конечны и равны, значит, существует общий предел.
– односторонние пределы конечны и равны, значит, существует общий предел.
3) 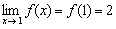 – предел функции в точке равен значению данной функции в данной точке.
– предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция 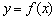 непрерывна в точке
непрерывна в точке 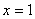 по определению непрерывности функции в точке.
по определению непрерывности функции в точке.
Ответ: функция непрерывна на всей числовой прямой, кроме точки 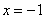 , в которой она терпит разрыв первого рода со скачком.
, в которой она терпит разрыв первого рода со скачком.
ЗАДАЧА 3.ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ФУНКЦИЙ

Таблица производных:
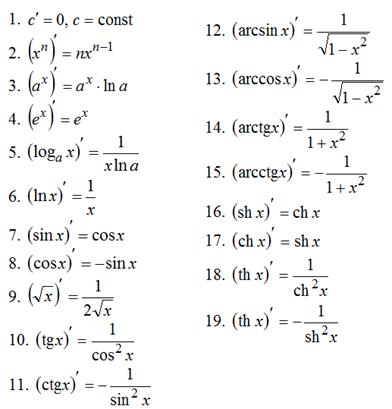
Таблица производных сложных функций
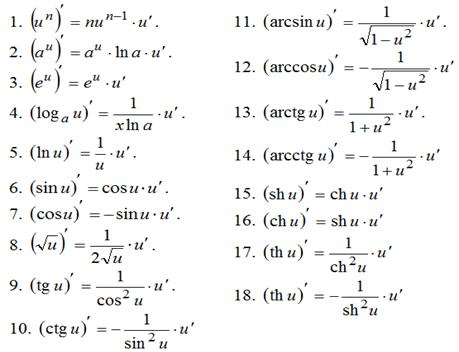
| Задание 1. | Найти производную функции 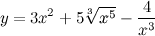 |
| Решение. | Для нахождения производной данной функции используем правила дифференцирования и таблицу производных. Так как производная суммы/разности равна сумме/разности производных, то 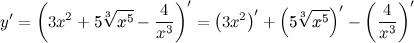 постоянный множитель можно вынести за знак производной постоянный множитель можно вынести за знак производной 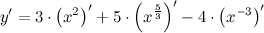 Воспользуемся формулой для производной степенной функции: Воспользуемся формулой для производной степенной функции: 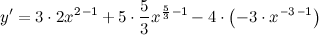 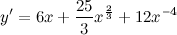 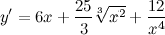 |
| Ответ. | 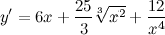 |
| Задание 2. | Найти производную функции 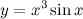 |
| Решение. | По правилу дифференцирования произведения получаем: 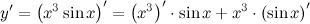 теперь воспользуемся формулами для производных степенной и тригонометрической функций: теперь воспользуемся формулами для производных степенной и тригонометрической функций: 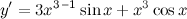 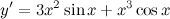 |
| Ответ. | 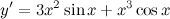 |
| Задание 3. | Найти производную функции 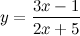 |
| Решение. | Воспользуемся правилом дифференцирования частного: 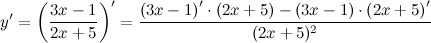 Производная суммы/разности равна сумме/разности производных и константу можно выносить за знак производной, поэтому имеем: Производная суммы/разности равна сумме/разности производных и константу можно выносить за знак производной, поэтому имеем: 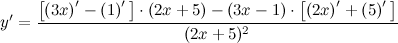 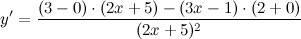 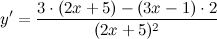 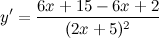 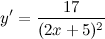 |
| Ответ. | 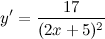 |
| Задание 4. | Найти производную функции 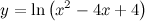 |
| Решение. | По свойству дифференцирования сложной функции вначале находим производную натурального логарифма и домножаем на производную подлогарифмической функции: 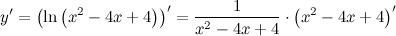 Производная суммы равна сумме производных и константу можно выносить за знак производной, поэтому имеем: Производная суммы равна сумме производных и константу можно выносить за знак производной, поэтому имеем: 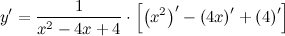 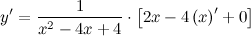 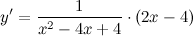 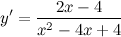 Знаменатель дроби можно свернуть по формуле квадрат разности, а в числителе двойку вынесем как общий множитель за скобки: Знаменатель дроби можно свернуть по формуле квадрат разности, а в числителе двойку вынесем как общий множитель за скобки: 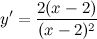 сокращаем: сокращаем: 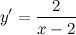 |
| Ответ. | 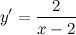 |
| Задание 5. | Найти производную функции 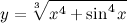 |
| Решение. | По свойству дифференцирования сложной функции и используя формулы вычисления производной показательной и тригонометрических функций, получим: 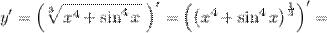 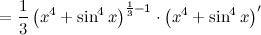 Производная суммы равна сумме производных: Производная суммы равна сумме производных: 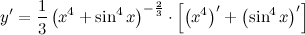 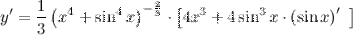 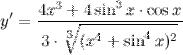 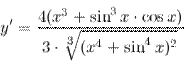 Для вычисления данной производной использовались правила дифференцирования и таблица производных сложных функций. Для вычисления данной производной использовались правила дифференцирования и таблица производных сложных функций. |
| Ответ. | 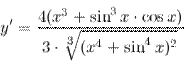 |
| Задание 6. | Найти производную функции 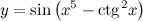 |
| Решение. | По правилу дифференцирования сложной функции: 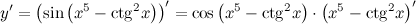 По правилу дифференцирования разности: По правилу дифференцирования разности: 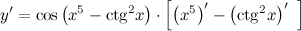 Производная Производная 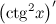 берется по правилу дифференцирования сложной функции: берется по правилу дифференцирования сложной функции: 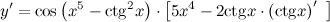 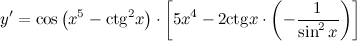 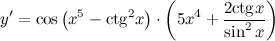 Для решения данной производной мы воспользовались правилами дифференцирования и таблицей производных сложных функций. Для решения данной производной мы воспользовались правилами дифференцирования и таблицей производных сложных функций. |
| Ответ. | 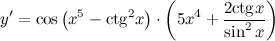 |
| Задание 7. | Найти производную функции 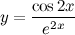 |
| Решение. | Сначала воспользуемся правилом дифференцирования частного: 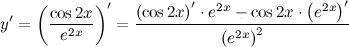 Затем каждую производную вычислим по правилу дифференцирования сложной функции: Затем каждую производную вычислим по правилу дифференцирования сложной функции: 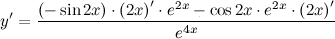 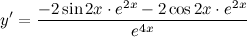 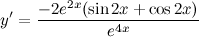 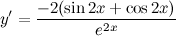 Таблица производных сложных функций - ссылка. Таблица производных сложных функций - ссылка. |
| Ответ. | 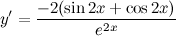 |
| Задание 8. | Найти производную функции 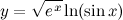 |
| Решение. | Перепишем исходную функцию в виде 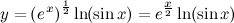 По правилу дифференцирования произведения имеем: По правилу дифференцирования произведения имеем: 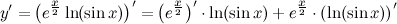 Затем находим производную по правилу дифференцирования сложной функции имеем: Затем находим производную по правилу дифференцирования сложной функции имеем: 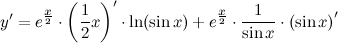 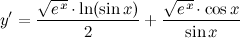 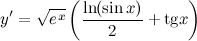 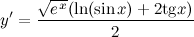 |
| Ответ. | 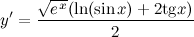 |
ЗАДАЧА 4.ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЕ ГРАФИКА
Пусть дана функция. Для её исследования нужно:
1) Найти её область определения. Если это не слишком сложно, то полезно найти также область значений. (Однако, во многих случаях, вопрос нахождения откладывается до нахождения экстремумов функции.)
2) Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной, не является ли она периодической.
3) Найти точки пересечения графика с осями координат, что состоит в простом вычислении значения функции при условии:
С осью ОX: y=0;
С осью ОY: x=0.
Нахождение точек пересечения с осью может привести к необходимости решить сложное алгебраическое уравнение, что, быть может, удастся сделать лишь приближённо. Отыскав корни функции и точки разрыва, мы можем определить знак функции на каждом из интервалов между этими точками. Это можно сделать либо вычислив значение функции в какой-нибудь из точек интервала, либо применив метод интервалов.
4) Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения, если такие граничные точки имеются. Если функция имеет точки разрыва, то эти точки тоже проверить на наличие вертикальных асимптот функции. Найти наклонные асимптоты.
5) Найти промежутки монотонности. Для этого находят производную и решают неравенство:
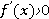 . На промежутках, где это неравенство выполнено, функция возрастает. Там, где выполнено неравенство
. На промежутках, где это неравенство выполнено, функция возрастает. Там, где выполнено неравенство 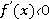 , функция убывает.
, функция убывает.
Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума: там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием - локальные минимумы.
6) Нахождение интервалов выпуклости и вогнутости ведётся с помощью второй производной. Найдя 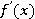 , мы определяем знаки
, мы определяем знаки 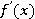 на интервалах:
на интервалах:
если 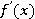 ›0, то кривая графика функции вогнута;
›0, то кривая графика функции вогнута;
если 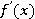 ‹0, то кривая графика функции выпуклая.
‹0, то кривая графика функции выпуклая.
Заодно определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).
7) Нахождение точек пересечения графика с асимптотой и дополнительных точек. Этот пункт не носит обязательного характера, однако нахождение таких точек придаёт исследованию функции и построенному её графику законченность и полноту.
Заметим, что получающиеся в процессе исследования функции точки на осях координат и на графике полезно сразу же наносить на чертёж. Это помогает по ходу дела уяснять вид графика.
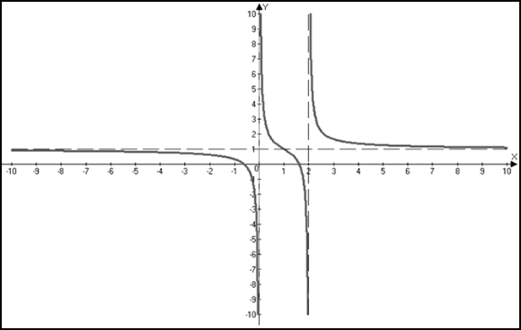
Пример 1. Исследовать функцию и построить ее график
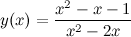
Решение. 1) Область определения функции.
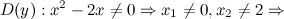
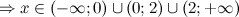
2) Четность, нечетность.
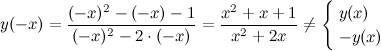
Функция общего вида.
3) Точки пересечения с осями.
а) с осью 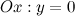 :
:
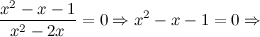
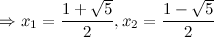
то есть точки 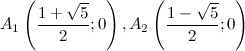
б) с осью 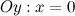 : в данной точке функция неопределенна.
: в данной точке функция неопределенна.
4) Асимптоты.
а) вертикальные: прямые 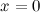 и
и 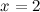 - вертикальные асимптоты.
- вертикальные асимптоты.
б) горизонтальные асимптоты:
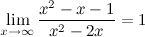
то есть прямая 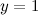 - горизонтальная асимптота.
- горизонтальная асимптота.
в) наклонные асимптоты 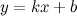 :
:
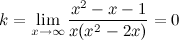
Таким образом, наклонных асимптот нет.
5) Критические точки функции, интервалы возрастания, убывания.
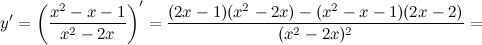
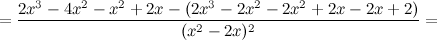
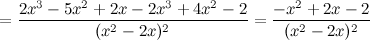
Найдем точки, в которых первая производная равна нулю или не существует: 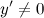 для любого
для любого  из области определения функции;
из области определения функции; 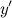 не существует при
не существует при 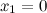 и
и 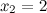 .
.

Таким образом, функция убывает на всей области существования. Точек экстремума нет.
6) Точки перегиба, интервалы выпуклости, вогнутости.
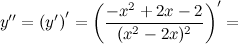
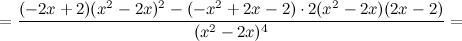
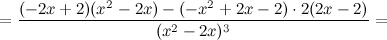
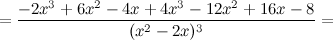
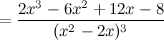
Найдем точки, в которых вторая производная равна нулю или не существует: 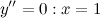 ; при
; при 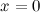 и
и 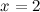 вторая производная не существует.
вторая производная не существует.
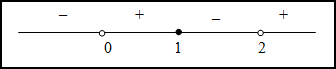
Таким образом, на промежутках 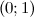 и
и 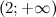 функция вогнута, а на промежутках
функция вогнута, а на промежутках 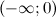 и
и 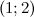 - выпукла. Так как при переходе через точку
- выпукла. Так как при переходе через точку 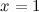 вторая производная поменяла знак, то эта точка является точкой перегиба.
вторая производная поменяла знак, то эта точка является точкой перегиба.
7) Находим дополнительные точки и строим эскиз графика.
ЗАДАЧА 5.ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
