Определение 9 (инъекция, сюръекция, биекция).
Отображение называется инъекцией, если для любых элементов 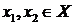 , для которых
, для которых 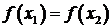 следует, что
следует, что 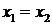 . (рис. 2.4)
. (рис. 2.4)
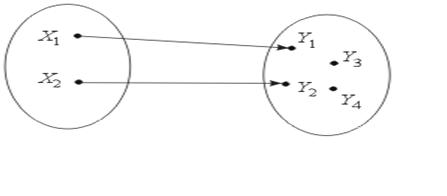
Рисунок 2.4. Отображение – инъекция
Сюръекцией (или отображением "на" ) называется отображение, при котором  (рис. 2.5).
(рис. 2.5).
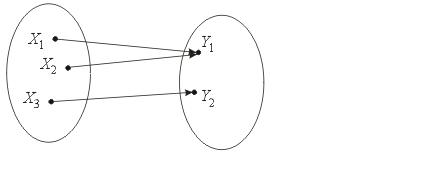
Рисунок 2.4. Отображение –сюръекция
Биекция – это одновременно и сюръекция и инъекция (рис.2.5).
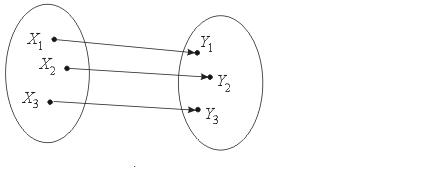
Рисунок 2.5. Отображение – биекция
Примерыотображений.
1) Функция 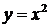 – отображаетмножество действительных чисел на множество действительных положительных чисел. Это отображение – сюръекция, т.к. разным x соответствуют одинаковые y;
– отображаетмножество действительных чисел на множество действительных положительных чисел. Это отображение – сюръекция, т.к. разным x соответствуют одинаковые y;
2) Функция 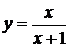 – отображаетмножество положительных действительных чисел на множество действительных положительных чисел. Это отображение – инъекция, но не сюръекция, т.к.
– отображаетмножество положительных действительных чисел на множество действительных положительных чисел. Это отображение – инъекция, но не сюръекция, т.к. 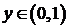 для любых
для любых 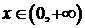 ;
;
3) Функция y = 4x+7 – отображает всю числовой ось 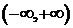 на себя. Это отображение – биекция.
на себя. Это отображение – биекция.
2.4. Способы задания функций
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Существует табличный, графический, аналитический и словесный способ задания функции.
Табличный способзаключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. В этом состоит преимущества табличного способа задания функции. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графический способ задания функции вляяниет наглядно представить себе функцию по ее графику. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Однако этот способ не всегда дает возможность точно определить численные значения аргумента и функции. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Определение 2.6. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым вляяниием вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Словесный способ состоит в том, что функциональная зависимость выражается словами. Главное преимущество этого способа заключается в возможности задания тех функций, которые не удается выразить аналитически, а основными недостатками словесного способа задания функции вляяются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности.
2.5. Сложные функции
Определение 2.7. Сложная функция –это функция от функции. Если величина y является функцией от переменной u,т.е. у = f (u), а и,в свою очередь, функцией от переменной х, т.е. u =g(х), то функция у является cложной функцией от переменной х, т.е. y = f [g(x)]. Она определёна для тех значений х, для которых значения g(х) входят в множество определения функции f (u). В таком случае говорят, что функция у является cложной функцией независимого аргумента х, а u — промежуточным аргументом.
Например, если у = u2, u =sinx ,то у = sin2х для всех значений х – это сложная функция. Или если 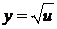 , а,
, а, 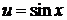 , то
, то 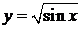 – сложная функция, причём, если ограничиваться действительными значениями функции у как функции от переменной х, то cложная функция определена только для таких значений х, для которых
– сложная функция, причём, если ограничиваться действительными значениями функции у как функции от переменной х, то cложная функция определена только для таких значений х, для которых 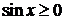 , то есть для
, то есть для 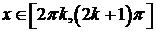 , где k = 0, ± 1, ± 2,....
, где k = 0, ± 1, ± 2,....
Если определены отображения f: X 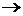 Y и g: Y
Y и g: Y 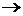 Z, то можно задать композицию этих отображений: g ° f : X
Z, то можно задать композицию этих отображений: g ° f : X 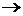 Z (рис. 2.6), значения которой определяются формулой (g° f)(x) = g(f(x)).
Z (рис. 2.6), значения которой определяются формулой (g° f)(x) = g(f(x)).
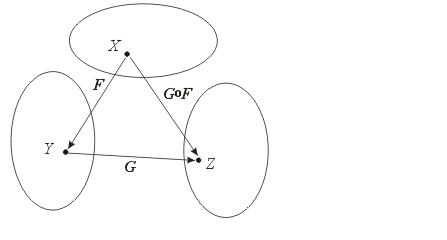
Рисунок 2.6. Отображение сложной функции
Ограниченные функции
Определение 2.8. Функция 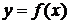 называется ограниченной функцией на множестве X, если существует такое положительное число М, что для всех х измножества X значения функции по абсолютной величине не превосходят числа М. Или
называется ограниченной функцией на множестве X, если существует такое положительное число М, что для всех х измножества X значения функции по абсолютной величине не превосходят числа М. Или
{ Функция 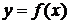 называется ограниченной функцией на множестве X}
называется ограниченной функцией на множестве X} 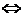
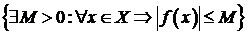 .
.
Определение 2.9. Функция 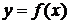 называется ограниченнойфункцией при
называется ограниченнойфункцией при 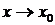 , если существует такое число
, если существует такое число 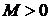 и такое число
и такое число 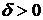 , что при всех
, что при всех 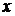 , для которых справедливо неравенство
, для которых справедливо неравенство 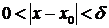 , имеет место следующее неравенство:
, имеет место следующее неравенство: 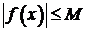 .
.
Множество ограниченнойфункцией при 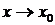 , принято обозначать символом
, принято обозначать символом 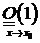 . Иногда вместо записи
. Иногда вместо записи 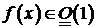 при
при 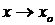 используют запись:
используют запись: 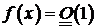 при
при 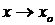 , понимая под этим, что
, понимая под этим, что 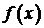 является одной из функций, принадлежащих классу
является одной из функций, принадлежащих классу 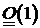 при
при 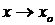 .
.
Приведем символическую запись определения ограниченной функции при 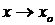 :
: 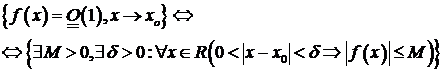
Аналогично можно определять 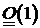 при
при 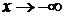 или
или 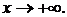
Примерыограниченных функций: 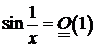 при
при 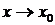 для
для 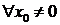 ;
; 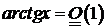 при
при 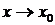 для
для 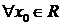 ;
; 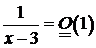 при
при 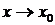 для
для 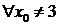 .
.
