Синтез комбинаторных систем.
Комбинаторной системой называется автомат выполняющий преобразование х в у, где
x = { x1, x2, …, xn } – множество входных булевых переменных
y = { y1, y2, …, yn } – множество выходных булевых функций
Отличительной особенностью комбинаторных систем является то, что выходной сигнал в момент времени T является функцией только входного сигнала в момент времени Т. В общем виде на стр-ных и функциональных схемах комбинаторные системы изображаются в виде перевернутой трапеции.
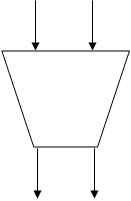 x1 xn
x1 xn
КС
у1 уn
КС представляет собой схемы, состоящие из логических элементов. Каждый логический элемент реализует элементарную булеву функцию. Минимальная совокупность логических элементов достаточное для реализации произв-ной системы называется эл-ным базисом.
Алгоритм синтеза логических функций с малым числом переменных в заданном базисе :
1. Функция записывается в сов. норм. дизъюнктивной форме по заданной таблице истинности
2. Находится мин. форма, любым способом.
3. Операции дизъюнкции, конъюкции и отрицания варажаются через функции базиса.
4. Записывается выражение функции в элементах базиса и строится схема.
Пример.
Функция задана таблицой истинности :
| x1 | x2 | x3 | f |
Минимизируем графическим методом :
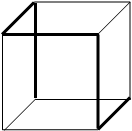 111 110
111 110
011 010
f ( x1, x2, x3 ) = x2x3 +  1x2 +
1x2 +  2
2  3
3
101 100
001 000
Реализуем функцию в базисе В6 = { у6, у7 }
у6(x1, x2) = x1 Å x2
y7(x1, x2) = x1  x2
x2
 | |||
 | |||
x1 x1
x2  у6 x2 1 у9
у6 x2 1 у9
Выразим в заданном базисе функцию отрицания у6(x, 1) = 
Выразим функцию конъюкции у6 (y7(y6, 1), у6(x2, 1),1) = x1x2
Запишем выражение искомой функции
f ( x1, x2, x3 ) = y7 [у6 (y7(y6(x2, 1), y6(x3, 1)),1),y6(y7(x2,x3),1), y6(y7(x1, y6(x2,1)),1)];
Построим схему данной функции :
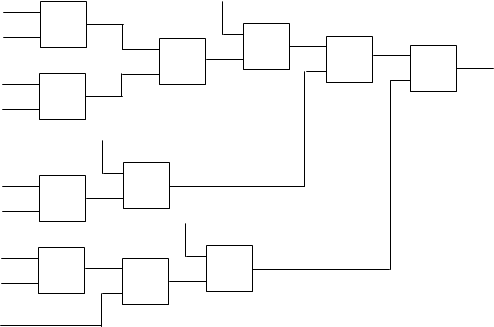 1 1
1 1
x2 11
1 1 f ( x1, x2, x3 )
x3 1
1
1
x2 1
x3 1
1
x2 1 1
x3
Если число аргументов функций велико, то описанный способ синтеза комбинаторных схем становится громоздким и трудоемким.
Для синтеза схем с большим числом переменных существуют более эффективные методы. Один из них :
МЕТОД КАСКАДОВ.
Основанием для метода является теор. Шиннона, исходя из которой произв. Функция может быть представлена в следующем виде :
f(x1, … , xn) =  i f(x1, …, xi-1,Æ,xi+1, …, xn)+f (x1, …,xi-1,1,xi+1,…, xn ) =
i f(x1, …, xi-1,Æ,xi+1, …, xn)+f (x1, …,xi-1,1,xi+1,…, xn ) =
=  i f ( Æ ) + xi f( 1 )
i f ( Æ ) + xi f( 1 )
Эту функцию можно реализовать следующей схемой :
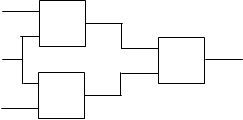 f1
f1
&
xi
1 f
&
f0
Это устройство – каскадный элемент, который на схемах обозначают в следующем виде :
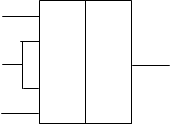 f1 &
f1 &
1
 x1 & f
x1 & f
f0
С помощью данного каскада получено представление от n аргументов, через остат-ные функции f0 и f1 для функций от n-1 аргумент, с помощью искл. хi перемен.
На втором шаге каскада реализуется искл. следующая перемен. И далее поступая также мы получим остат – ные функции.
Это – каскадный метод – при этом каждый каскад соответствует исключению некоторой переменной. Для одной и той же функции можно получить несколько реализаций. Число реализаций равно :
N ( N - 1)( N – 2) - … = n!
Отсюда следует, что найти самую эффективную реализацию простым перебором весьма затруднительно.
Поэтому для метода должна быть найдена эффективная стратегия. Это позволяет сделать аппарат произв – ных от булевых функций. Пр – ная от функции n-аргументов.
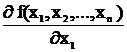 =f (x1,…, xi-1,Æ,xi+1,…, xn)Åf (x1, …, xi-1,1,xi+1, …, xn)
=f (x1,…, xi-1,Æ,xi+1,…, xn)Åf (x1, …, xi-1,1,xi+1, …, xn)
Пример :
Найти пр-ную от функции двух переменных
f (x1,x2) = x1 + x2
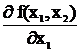 = x2 Å (1 + x2) =
= x2 Å (1 + x2) =  2
2
Повторные пр-ные определяются следующим образом :
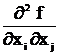 =
= 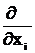 (
( 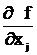 ) и т. д.
) и т. д.
Пр-ная от булевой функции определяет условия при которых функция зависит от хi
f (x1,…, xi-1,Æ,xi+1,…, xn) ¹ f (x1, …, xi-1,1,xi+1, …, xn) т.е. при изменении хi меняется значение функции. ( функция зависит от перем.)
Если пр-ная равна 0, то функция от хi не зависит, т.е. при изменении хi значение функции не меняется.
Рассмотрим пример:
f (x1, x2, x3, x4) = x1x2x3 +  1х4 + x2x3 + x1
1х4 + x2x3 + x1  3x4
3x4
Определить при каких условиях функция зависит от переменной х3. Найдем соответствующую производную :

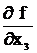 = (
= (  1х4 +х1х4) Å (х1х2 +
1х4 +х1х4) Å (х1х2 +  1х4 +х2) = х4 Å ( х2+
1х4 +х2) = х4 Å ( х2+  1х4) =
1х4) =
= х4  2
2  1х4 +
1х4 +  4 ( х2+
4 ( х2+  1х4 ) = х4
1х4 ) = х4  2 (х1+
2 (х1+  4) +
4) +  4х2 =
4х2 =  4х2 + х4
4х2 + х4  2х1
2х1
Ответом на поставленную задачу будут значения х1, х2 , х4 при которых
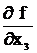 = 1.
= 1.
Составим соответствующую таблицу:
| х1 | х2 | х4 | 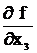 |
| х1 | х2 | х4 | 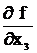 |
На этих наборах функция зависит от переменной х3.
Первый шаг каскадной реализации.
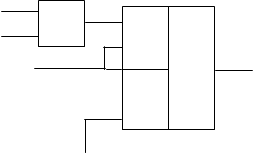 |
х1 & & 1
х4
&
f0
f0 ( x1,x3,x4 ) =  1 +
1 +  3
3  4 + x3x4 =
4 + x3x4 =  1 +
1 + 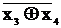
Введем определение :
Весом пр-ной функции называется количество возможных наборов, при которых производная равна 1. Исходя из предыдущего примера сложность производной по х3 ( 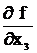 ) равна 3.
) равна 3.
Запишем утверждение :
Чем больше состояний имеет функция, прикоторых она зависит от xi, тем сильнее она зависит от этой переменной.
Для примера выясним от какой переменной функция зависит сильнее.
f ( x1, x2, x3,x4 ) = x1x2x3 +  1x4 + x2x3 + x1
1x4 + x2x3 + x1  3x4
3x4
W ( 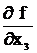 ) = 3
) = 3
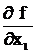 = ( x4 +x2x3 ) Å (x2x3 +
= ( x4 +x2x3 ) Å (x2x3 +  3x4 )
3x4 )
| х1 | х2 | х4 | 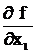 |
W ( 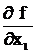 ) = 1
) = 1
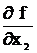 = (
= (  1x4 + x1
1x4 + x1  3x4 ) Å ( x1x3 +
3x4 ) Å ( x1x3 +  1x4 + x3 + x1
1x4 + x3 + x1  3x4 ) =(x4
3x4 ) =(x4  1 + x4
1 + x4  3) Å ( x3 + x4 )
3) Å ( x3 + x4 )
| х1 | х2 | х4 | 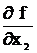 |
W ( 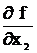 ) = 3
) = 3
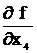 =(x1x2x3 + x2x3)Å(x1x2x3 +
=(x1x2x3 + x2x3)Å(x1x2x3 +  1 + x2x3 + x1
1 + x2x3 + x1  3) = x2x3Å(x2 +
3) = x2x3Å(x2 +  1 +
1 +  3 )
3 )
| х1 | х2 | х4 | 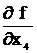 |
W ( 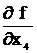 ) = 5
) = 5
Оказалось, что сильнее всего функция зависит от переменной х4. При этом видно, что чем сильнее зав-ть функции, тем меньше сложность ост-ной функции при ее искл-нии.
Для функции заданной таблично удобно использовать следующий метод определения веса производной:
Рассмотрим на примере :
Функция от четырех переменных задана таблицей истинности :
| х1 | х2 | x3 | x4 | f |
Для заданной функции определить веса производных по х1, х2, х3, х4.
| x2 | x3 | x4 | d | ||
Cтолбцы 1 и 0 заполняются следующим образом :
Вместо искл. переменной в каждый набор подставляются значения 1 или 0 и выписывают соотв. стб. знач. Функции из исходной таблицы.
Столбец d получается сложением по mod 2 соотв. знач. стб. 1 и 0.
W1 = 5
x2 :
| x1 | x3 | x4 | d | ||
W2 = 3
x3 :
| x1 | x2 | x4 | d | ||
W3 = 3
x4 :
| x1 | x2 | x3 | d | ||
W4 = 5
Анализ производных показал, что для данного примера первыми исключ-ми переменными будут х1 и х4.
Рассмотрим более сложную задачу для которой функция задана аналитически ( от 5-и переменных ).
f ( x1, x2, x3, x4, x5 ) = x1  2x3 +
2x3 +  1
1  3x4 + x1x3
3x4 + x1x3  5 + x1x2x4 +
5 + x1x2x4 +  2x3x5 +
2x3x5 +  3
3  4x5
4x5
Для данного примера на картах Карно определим веса производных и первую искл. переменную. Затем на картах Карно определим вторую исключаемую переменную и т.д., а затем по полученным данным построим принц. Схему функции.

X1X2 x3X4X5 001 011 010 110 111 101 100
W1 = 7 ; W2 = 5 ; W3 = 9 ; W4 = 5 ; W5 = 7 ;
Первая искл. переменная х3
 Рассмотрим карту Карно для остальных функций : f ( 1 ) f ( 0 )
Рассмотрим карту Карно для остальных функций : f ( 1 ) f ( 0 )
X1X2 X4X5 00 01 11 10
| f (0) 00 | |||||
W1 = 2 ; W2 = 2 ; W4 = 4 ; W5 = 4 ;
 |
X1X2 X4X5 00 01 11 10
| f (1) 00 | |||||
W1 = 5 ; W2 = 3 ; W4 = 1 ; W5 = 3 ; Искл. х1
Второй искл. переменной - х4 или х5.
Получим f (1,0) f (1,1).
 x2 x4 x5 00 01 11 10
x2 x4 x5 00 01 11 10
| 0 | ||||
| 1 |
f11 =  2 +
2 +  5 + x4 =
5 + x4 = 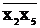 + x4
+ x4
 x2 x4 x5 00 01 11 10
x2 x4 x5 00 01 11 10
| 0 | ||||
| 1 |
f10 =  2 x5
2 x5
Функции f(0,0) и f(0,1) получ. искл. х4.
f00 = х5 f01 =  1 + х2
1 + х2
По имеющимся данным строим принц. схему каск. метода :
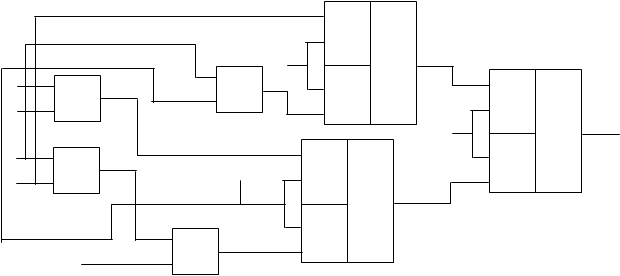 f 00
f 00
& 1
1 x4 f 0 & 1
& f 01
f 10 x3 f
x4 & & 1 f 1 &
x5 x1
&
x4 & f 11
f00 = х5 f01 =  1 + х2
1 + х2
