Основные операции алгебры буля.

(АЛГЕБРЫ ЛОГИКИ).

ТАБЛИЦЫ ИСТИННОСТИ ЭТИХ ОПЕРАЦИЙ.

1. « НЕ » - х

0 1

1 0

2. х₁ х₂ « ИЛИ »

х1 х2	х1 х2
0 0
0 1
1 0
1 1

3. Конъюкция х₁& х₂ « И »

х1 х2	х1& х2
0 0
0 1
1 0
1 1

4. Импликация х₁® х₂ « ЕСЛИ ТО »

х1 х2	х1® х2
0 0
0 1
1 0
1 1

5. Эквиваленция х₁ ~ х₂ « ТОГДА И ТОЛЬКО ТОГДА »

х1 х2	х1 ~ х2
0 0
0 1
1 0
1 1

ПРЕДСТАВЛЕНИЕ ФУНКЦИИ В АЛГЕБРЕ БУЛЯ.

Функция трех переменных :

x1	x2	x3	f

Кроме табличного задания алгебры логики применяются различные аналитические методы. К ним относятся – дизъюктивная и коньюктивная форма. Для представления в дизъюктивной соверш. норм. форме (ДСНФ) вводится фар-кая функция единицы, которая соответствует конституентам, в которых функция принимает значение = 1.

Единичная функция записывается ,как элементарная конъюнкция, содержащая n – переменных и называется минитермом. Алгоритм представления функции алгебры логики в виде ДСНФ записывается в виде:

1) Выбрать в таблице функции все наборы аргументов , на которых функция обращ. в единицу

2) Вычислить конъюкцию, соответствующей этим наборам аргументам. При этом аргумент x_i входит в данный набор как 1 , он вписывается без изменения в конъюнкцию, соответствующую данному набору. Если х_i входит как 0 ,то в конъюнкцию вписывается его отриц.

3) Все полученные конъюнкции соединены между собой знаками дизъюнкции.

Для примера запишем ДСНФ

f(х₁,х₂, х₃) = _{1 2 3 1} x_{2 3 1 2} x₃ x_{1 2 3} x_{1 2} x₃

x₁ x_{2 3}

Для представления функции алгебры логики в КСНФ вводится хар-кая

функция О ,которая соответствует набору, на котором функция принимает значение О. Функция нуля записывается как элементарная дизъюнкция, содержащая n-переменных и называется макситермом.

Алгоритм построения КСНФ:

1) Выбрать в таблице функции все наборы аргументов , на которых функция обращается в О.

2) Выписать дизъюнкции, соответствующие этим наборам. При этом если х_i входит как О, он вписывается без изменений в дизъюнкцию, если х_i входит как 1, то в дизъюнкцию вписывается его отрицание.

Для примера запишем КНФ

f(х₁,х₂, х₃) = (x₁ x_{2 3} ) & ( _{1 2 3})

По аналогии с теорией множеств при минимизации:

ДСНФ ® ДНФ

КСНФ ® КНФ

ДНФ,КНФ – обозначения для сокращения макситермами и минитермами. Номера мини- и макситермов являются дес-ными экв-ми соответствующего набора, на котором функция принимает 1 или 0 соответственно, то есть

(ДСНФ) f( х₁,х₂,х₃ ) = m₀ m₂ m₃ m₄ m₅ m₆

(КСНФ) f( х₁,х₂,х₃ ) = m₁ & m₇

Согласно теореме Шеннона функция в ДСНФ имеет вид :

f( х₁,…,х_k ) = 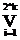f( d₁,…,d_k ) & x₁^d1* x₂^d2… x_k^dk

Функция трех переменных задана таблично :

x1	x2	x3	f

f(х₁,х₂, х₃) = _{1 2 3 1} x_{2 3 1}x₂ x₃ x₁ x₂ x₃ (ДСНФ)

Выясним каково количество возможных булевых функций к-значных.

Если мы имеем к переменных, то из них можно составить m=2^к комбинаций, а так как для каждой комбинации может быть задана своя функция, то общее число возможных функций V=2^m=2^{2^k}

Теорема :

Алгебра множеств с к-порожденными множествами изоморфна к-значной алгебре Буля.

Доказательство:

Изоморфизм строится следующим образом:

j (М_i)=x_i - для алгебры множеств

j (f_i)=y_i - для алгебры Буля

Тогда согласно представлению Булевых функций в ДСНФ и представлению функций от порождающих множеств в СНФК следует следующее :

f_j(M_i) = 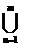M_v^dv ;

y_j(x_i) = 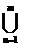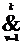x_v^dv ;

Основным следствием этой теоремы является возможность применения всех методов минимизации из теории множеств для алгебры Буля.

Метод Квайна для функции Буля :

0 0 0

0 1 0 0х0

0 1 1 х11

1 1 1

Строим таблицу Квайна :

0х0
х11

Y(x₁, x₂, x₃) = _{1 3} x₂x₃

Минимизация по методу Карно :

х1 х2х3

f(x₁, x₂, x₃) = _{1 3} x₂x₃