Минимизация функции с помощью карт карно.
Графический способ минимизации удобен для трех ,четырех переменных, а для функции пяти переменных и выше применение графического метода невозможно.
Поэтому для использования принципа этого метода для большеге количества переменных предложена модернизация.
Идея: развернуть куб на плоскости
000 001 011 010 000
100 101 111 100 100
 Исходя из развертки куба , строится таблица:
Исходя из развертки куба , строится таблица:
 М1 М2М3 00 01 М3 11 10
М1 М2М3 00 01 М3 11 10
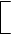 1 1 |
 М1
М1
М2
Построенная таблица – карта КАРНО.
В ней отмечены конституенты,присутствующие в функции, подобно тому, как отмеченные вершины куба объеденены в ребра и грани.
Объед. и еден. карты (интервалы).
Объединение единиц в интнрвалы в карте иначе называют склеиванием.
Этапы заполнения карты КАРНО.
1. Все конституенты , присутствующие в функции заносятся в карту с помощью единиц в соответствующие клетки.
2. Выделяют интервалы на карте по следующим принципам:
а) в один интервал объединяют только соседние единицы по вертикали или горизонтали;
б) в один интервал можно объеденить 2к единиц, где k=0,1,2,3,4,….
в) карта циклически замкнута по вертикали и горизонтали.
г) в выделенный интервал объединено максимально возможное количество единиц.
Всего на карте выделено 3 интервала, в каждый входят те минитермы в которых он полностью находится.
Запишем минимальную функцию:
f(M1,М2,М3) = М1М3 + М2М3 + М1  2
2  3
3
Пример:
Минимизировать функцию:
f(M1,М2,М3)=  1
1  2
2  3 + М1
3 + М1  2
2  3 +
3 +  1
1  2 М3 + М1
2 М3 + М1  2 М3 + М1М2М3 +
2 М3 + М1М2М3 +
+  1М2
1М2  3 + М1М2
3 + М1М2  3
3
 00 01 М3 11 10
00 01 М3 11 10
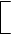 1 1 |
 М1
М1
М2
f(M1,М2,М3) =  2 + М1 +
2 + М1 +  3
3
При правильном объединении функцию больше минимизировать невозможно.
 Карта Карно для 4-х переменных:
Карта Карно для 4-х переменных:
М1М2 М3М4 00 01 11 10
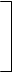 00 00 | |||||
| М2 | |||||
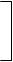 11 11 | |||||
| М1 |

 М3
М3
М4
f(M1,М2,М3) = М1М4 + М2М4 +  1
1  2
2  4
4
Пример:
 f(M1,М2,М3,М4 ) (3,4,5,7,9,11,12,13 конституенты)
f(M1,М2,М3,М4 ) (3,4,5,7,9,11,12,13 конституенты)
М1М2 М3М4 00 01 11 10
3 - 0011 4 - 0100 5 - 0101 7 - 0111 9 - 1001
11- 1011 12 - 1100 13 - 1101
f(M1,М2,М3,М4 )= М2  3+
3+  1М3М4 +М1
1М3М4 +М1  2М4
2М4
Карты Карно для 5-ти переменных:


 М4 М5
М4 М5
 М1М2 М3М4М5 001 М3 011 010 110 111 101 100
М1М2 М3М4М5 001 М3 011 010 110 111 101 100
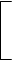 01 01 | ||||||||
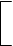 М2 11 М2 11 | ||||||||
| М1 10 |
При выделении интервалов необходимо соблюдать дополнительные правила:
1) Все интервалы должны быть симметричны относительно исходных размеров карт;
2) Если 2 единицы находятся симметрично границы раздела они считаются соседними.
f(М1,М2,М3,М4,М5) = М2  3 М5 + М1
3 М5 + М1  3 М4 М5 + М1
3 М4 М5 + М1  2 М3М4
2 М3М4  5
5
f(М1,М2,М3,М4,М5) =  1 М2
1 М2  3
3  4М5 +
4М5 +  1 М2
1 М2  3 М4 М5 +
3 М4 М5 +
+ М1М2  3
3  4 М5 + М1 М2
4 М5 + М1 М2  3 М4 М5 + М1
3 М4 М5 + М1  2
2  3
3  4 М5 +
4 М5 +
+ М1  2
2  3 М4 М5 +
3 М4 М5 +  1 М2
1 М2  3 М4
3 М4  5 + М1 М2
5 + М1 М2  3 М4
3 М4  5 +
5 +
+  1М2М3 М4
1М2М3 М4  5 + М1 М2М3 М4
5 + М1 М2М3 М4  5 + М1
5 + М1  2М3 М4 М5 +
2М3 М4 М5 +
+ М1  2М3
2М3  4 М5
4 М5

М1М2 М3М4М5 001 011 010 110 111 101 100
f(М1,М2,М3,М4,М5) = М2  3 М5 + М2 М4
3 М5 + М2 М4  5 + М1
5 + М1  2 М5
2 М5
Аппарат работы с картами и их преимущество.
1) Простота применения .
2) Наглядность расположения интервалов.
Недостатки:
1) Сложность работы возростает намного быстрее, чем увеличивается число элементов функции.
2) Трудоемкость алгоритмизации.
Исходя из недостатков следует, что для работы с функциями большего числа переменных нужны иные методы, причем они должны быть не графическими а аналитическими.
Для компьюторной технологии существует отличный от рассмотренного метода минимизации множеств ,который называется метод Квайна.
