Метод подбора эмпирических формул

В процессе экспериментальных измерений получают статистический ряд измерений двух величин, объединяемых функцией

y=f(x) (1)

Каждому значению функции y₁,…, y_n соответствует определенное значение аргумента x₁, x₂,…,x_n.

На основе экспериментальных данных можно подобрать алгебраические выражения, которые называют эмпирическими формулами. Такие формулы подбирают лишь в пределах измерений значений аргумента x₁,…,x_n. Эмпирические формулы имеют тем большую ценность, чем больше они соответствуют результатам эксперимента.

К эмпирическим формулам предъявляют два основных требования: по возможности они должны быть наиболее простыми и точно соответствовать экспериментальным данным в пределах изменения аргумента.

Таким образом, эмпирические формулы являются приближенными выражениями аналитических формул. Замену точных аналитических выражений приближенными, более простыми называют аппроксимацией, а функции – аппроксимирующими.

Процесс подбора эмпирических формул состоит из двух этапов. На первом этапе данные измерений наносят на сетку прямоугольных координат, соединяют экспериментальные точки плавной кривой и выбирают ориентировочно вид формулы. На втором этапе вычисляют параметры формул, которые наилучшим образом соответствовали бы принятой формуле. Подбор эмпирических формул необходимо начинать с самых простых выражений.

Результаты измерений многих явлений и процессов аппроксимируются простейшими эмпирическими уравнениями прямой:

y=a+bx, (2)

где a, b – постоянные коэффициенты.

Поэтому при анализе графического материала необходимо по возможности использовать линейную функцию. В этом случае применяют метод выравнивания. Он заключается в том, что кривую, построенную по экспериментальным точкам, представляют линейной функцией.

Для преобразования некоторой кривой (1) в прямую линию вводят новые переменные X и Y:

X=f₁(x,y); Y=f₂(x,y). (3)

В этом уравнении X и Y должны быть связаны линейной зависимостью

Y=a+bX. (4)

Для определения параметров прямой можно в уравнение (4) подставить координаты двух крайних точек, взятых с графика. Получают систему двух уравнений, из которых вычисляюта и b. После установления параметрова и bполучают эмпирическую формулу (4), которая связывает Y и X, что позволяет установить функциональную связь между х и у (3) и эмпирическую зависимость (1).

Линеаризацию кривых можно легко осуществить на полу- или логарифмических координатных сетках, которые сравнительно широко применяют при графическом методе подбора эмпирических формул.

Таким образом, аппроксимация экспериментальных данных прямолинейными функциями позволяет просто и быстро установить вид эмпирических формул.

Графический метод выравнивания может быть применен в различных случаях, когда экспериментальная кривая на сетке прямоугольных координат имеет вид плавной кривой. Рассмотрим основные случаи.

1. y=ax^b (степенная функция). (5)

ЗаменяяX=lg(x)иY=lg(y), имеемY=lg(a)+bX.

При этом экспериментальная кривая превращается в прямую линию на логарифмической сетке.

2. y=ae^bx(показательная функция). (6)

ЗаменяяY=lg(y) ,имеемY=lg(a)+xblg(e)

3. y=ax^b+c. (7)

a) b – задано. Принимая X=x^b, имеем прямую линию на сетке прямоугольных координат:

y=aX+c.

б) b – неизвестно. Принимая X=lg(x)и Y=lg(y-c),имеем прямую линию на логарифмической сетке:

Y=lg(a)+bX.

В этом случае необходимо предварительно вычислить с. Для этого по экспериментальной кривой принимают три произвольные точки: x₁y₁; x₂y₂и 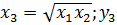метод подбора эмпирических формул - student2.ru и вычисляют с:

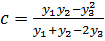метод подбора эмпирических формул - student2.ru (8)

4. y=ae^bx+c (9)

ЗаменяяY=lg(y-c), имеемпрямуюнаполулогарифмическойсеткеY=lg(a)+bxlg(e). Необходимо предварительно определить с помощью (8), при этом x₃=0.5(x₁+x₂).

5. y=a+(b/x) (10)

Заменяя x=(1/z), получаем прямую линию на сетке прямоугольных координат:

y=a+bz.

6.y=1/(a+bx). (11)

Заменяя y = 1/z, имеем z=a+bx, т.е. прямую на сетке прямоугольных координат.

7. y=1/(a+bx+cx²) (12)

Заменяяy=1/z, имеемz=a+bx+cx².

8. Сложную степенную функцию

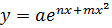метод подбора эмпирических формул - student2.ru (13)

преобразуем в прямую линию.

При lg(y)=z, lg(a)=P, nlg(e)=q, mlg(e)=zимеем z=p+qx+rx².

С помощью выражений (5) и (13) практически всегда можно подобрать уравнение эмпирической формулы.

На основе этих данных строим график (рис.6). Как видно из рисунка (6), имеем типичный график для показательной функцииy=ae^bx. В этой формуле необходимо найти параметры a и b.

метод подбора эмпирических формул - student2.ru

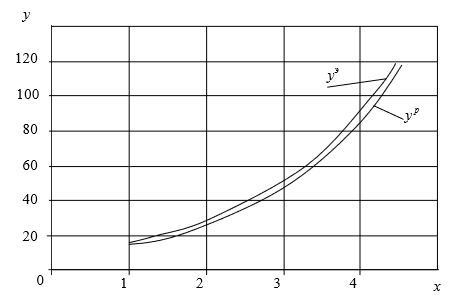
Рис. 6. Экспериментальная и расчетная кривые

Пример. Подобрать эмпирическую формулу для следующих измерений:

x		1,5	2,0	2,5	3,0	3,5	4,0	4,5
y	15,2	20,6	27,4	36,7	49,2	66,0	87,4	117,5

После логарифмирования этого выражения имеем lg(y)=lg(a)=bxlg(e). Если обозначить lg(y)=Y, то Y=lg(a)+bxlg(e), т.е. в полулогарифмических координатах выражение для Y представляет собой прямую линию.

Подставим в уравнение координаты крайних точек: lg15.2=lg(a)+blg(e), lg117.5=lg(a)+4.5blg(e)или lg(a)+blg(e)=1.183, lg(a)+4.5blg(e)=2.070.Учитывая, что e=2.718, lg(e)=0.434получим 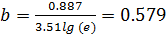метод подбора эмпирических формул - student2.ru ,lg(a)=1.183-0.254=0.929, a=8.45.