Параметрические методы испытания гипотез
Таблица нормального распределения
| z | 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 0,0 | 0,500 | 0,496 | 0,492 | 0,488 | 0,484 | 0,480 | 0,476 | 0,472 | 0,468 | 0,464 |
| 0,1 | 0,460 | 0,456 | 0,452 | 0,448 | 0,444 | 0,440 | 0,436 | 0,432 | 0,429 | 0,425 |
| 0,2 | 0,421 | 0,417 | 0,413 | 0,409 | 0,405 | 0,401 | 0,397 | 0,394 | 0,390 | 0,386 |
| 0,3 | 0,382 | 0,378 | 0,374 | 0,371 | 0,367 | 0,363 | 0,359 | 0,356 | 0,352 | 0,348 |
| 0,4 | 0,345 | 0,341 | 0,337 | 0,334 | 0,330 | 0,326 | 0,323 | 0,319 | 0,316 | 0,312 |
| 0,5 | 0,309 | 0,305 | 0,302 | 0,298 | 0,295 | 0,291 | 0,288 | 0,284 | 0,281 | 0,278 |
| 0,6 | 0,274 | 0,271 | 0,268 | 0,264 | 0,261 | 0,258 | 0,255 | 0,251 | 0,248 | 0,245 |
| 0,7 | 0,242 | 0,239 | 0,236 | 0,233 | 0,230 | 0,227 | 0,224 | 0,221 | 0,218 | 0,215 |
| 0,8 | 0,212 | 0,209 | 0,206 | 0,203 | 0,200 | 0,198 | 0,195 | 0,192 | 0,189 | 0,187 |
| 0,9 | 0,184 | 0,181 | 0,179 | 0,176 | 0,174 | 0,171 | 0,169 | 0,166 | 0,164 | 0,161 |
| 1,0 | 0,159 | 0,156 | 0,154 | 0,152 | 0,149 | 0,147 | 0,145 | 0,142 | 0,140 | 0,138 |
| 1,1 | 0,136 | 0,134 | 0,131 | 0,129 | 0,127 | 0,125 | 0,123 | 0,121 | 0,119 | 0,117 |
| 1,2 | 0,115 | 0,113 | 0,111 | 0,109 | 0,107 | 0,106 | 0,104 | 0,102 | 0,100 | 0,099 |
| 1,3 | 0,097 | 0,095 | 0,093 | 0,092 | 0,090 | 0,089 | 0,087 | 0,085 | 0,084 | 0,082 |
| 1,4 | 0,081 | 0,079 | 0,078 | 0,076 | 0,075 | 0,074 | 0,072 | 0,071 | 0,069 | 0,068 |
| 1,5 | 0,067 | 0,066 | 0,064 | 0,063 | 0,062 | 0,061 | 0,059 | 0,058 | 0,057 | 0,056 |
| 1,6 | 0,055 | 0,054 | 0,053 | 0,052 | 0,051 | 0,049 | 0,048 | 0,047 | 0,046 | 0,046 |
| 1,7 | 0,045 | 0,044 | 0,043 | 0,042 | 0,041 | 0,040 | 0,039 | 0,038 | 0,038 | 0,037 |
| 1,8 | 0,036 | 0,035 | 0,034 | 0,034 | 0,033 | 0,032 | 0,031 | 0,031 | 0,030 | 0,029 |
| 1,9 | 0,029 | 0,028 | 0,027 | 0,027 | 0,026 | 0,026 | 0,025 | 0,024 | 0,024 | 0,023 |
| 2,0 | 0,023 | 0,022 | 0,022 | 0,021 | 0,021 | 0,020 | 0,020 | 0,019 | 0,019 | 0,018 |
| 2,1 | 0,019 | 0,017 | 0,017 | 0,017 | 0,016 | 0,016 | 0,015 | 0,015 | 0,015 | 0,014 |
| 2,2 | 0,014 | 0,014 | 0,013 | 0,013 | 0,013 | 0,012 | 0,012 | 0,012 | 0,011 | 0,011 |
| 2,3 | 0,011 | 0,010 | 0,010 | 0,010 | 0,010 | 0,009 | 0,009 | 0,009 | 0,009 | 0,008 |
| 2,4 | 0,008 | 0,008 | 0,008 | 0,007 | 0,007 | 0,007 | 0,007 | 0,007 | 0,007 | 0,006 |
| 2,5 | 0,006 | 0,006 | 0,006 | 0,006 | 0,006 | 0,005 | 0,005 | 0,005 | 0,005 | 0,005 |
| 2,6 | 0,005 | 0,005 | 0,004 | 0,004 | 0,004 | 0,004 | 0,004 | 0,004 | 0,004 | 0,004 |
| 2,7 | 0,003 | 0,003 | 0,003 | 0,003 | 0,003 | 0,003 | 0,003 | 0,003 | 0,003 | 0,003 |
| 2,8 | 0,003 | 0,002 | 0,002 | 0,002 | 0,002 | 0,002 | 0,002 | 0,002 | 0,002 | 0,002 |
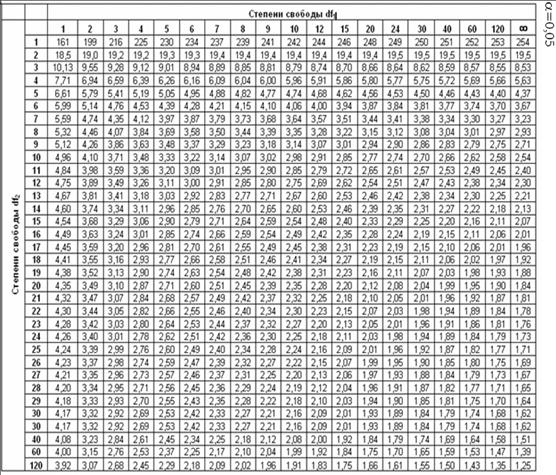
Критическое значение F-параметра .
1.Частная компания производит различные промышленные крепежные детали. Одним из видов выпускаемой продукции является противомагнитный болт. Болты производятся со средней длиной 5 см с известным стандартным отклонением в 0,05 см. Из последнего выпуска продукции была взята выборка объемом 25 единиц. Средняя длина болтов в выборке оказалась равной 5,025 см. Какие выводы могут быть сделаны о средней длине болтов в этом производственном выпуске?
2.Частная компания выпускает прохладительные напитки. На данный момент она производит поллитровые бутылки лимонада. Наполняющая машина установлена так, что наполняемость бутылки равна 500 мл. Каждый час отбираются наугад 30 бутылок и проверяются для того, чтобы определить, соответствует ли содержимое, необходимому объему. Средний объем в последней выборке равняется 495, 6 мл и стандартное отклонение составляет 8,3 мл. Имеется ли основание предполагать, что требуется переналадка машины?
3. Компания по производству новых электронных компонентов уверена, что 95% выпускаемых изделий соответствуют требованиям стандарта. Недавно компания ввела новые процедуры контроля качества. Для оценки эффективности таких процедур менеджер отобрал случайно 27 компонентов и исследовал их. Он нашел 2 бракованных изделия. Можно ли заключить на основе только этого факта, что процент годных изделий не уменьшился?
4. Компания производит электрические лампочки. Для определенного типа лампочек установлен нормативный срок использования 1500 ч. Для испытания новой партии была взята выборка 10 лампочек. Среднее время пользования лампочкой в выборке равна 1410 ч со стандартным отклонением 90 ч. Свидетельствуют ли эти данные о том, что ожидаемый срок использования изменился по сравнению с 1500 ч?
5. Частная компания была уполномочена провести опрос потребительского рынка для выявления предпочтений двух марок моющихся средств. При этом из 200 опрошенных 90 предпочли марку «А», а 80 марку «В», остальные затруднились с ответом. Есть ли расхождения между предпочтениями марок моющихся средств.
6. Высота отдельных ростков рассады распределена нормально со средней 53 см со стандартным отклонением 3 см. В прошлом году в ящик, в котором были высажены 15 таких растений была внесена по ошибке двойная норма удобрения. Средняя высота рассады в этом ящике достигла 55 см. Есть ли какое-либо основание предполагать, что повышенное внесение удобрений далоположительный эффект?
7. Внешний аудитор проверяет систему учета малой компании. Первая проверка из ста сделок показала, что 56 сделок ошибочны. Компании предоставили месяц для исправления . Когда аудитор провел вторую проверку, он обнаружил, что 28 сделок ошибочны из 78 проверенных сделок. Есть ли основание предполагать, что доля ошибок изменилась между проверками.
8. Поставщик электронных компонентов производит продукцию, которая иногда сразу отказывает. Он попытался контролировать производственный процесс так, чтобы доля неисправной продукции была меньше, чем 4%. Из поставляемой партии 500 компонентов 28 оказались неисправными. Имеется ли какое-нибудь основание предполагать, что производственный процесс вышел из под контроля и производится много неисправных изделий?
Лабораторная работа №5
Задача 1. Для участия в обучающей игре по знанию английского языка учащиеся 8-х классов были разбиты на две группы из 11 и 12 человек. Согласно требованию игры, необходимо, чтобы дисперсия уровня подготовки по языку была в группах одинакова. Для проверки был проведен экспресс-тест знания языка, который показал следующие баллы. Оценить изменчивость знаний в двух группах
| Группа 1 | ||||||||||||
| Группа 2 |
Задача 2. На основании данных предыдущей задачи сопоставить уровень знаний в двух группах
Задача 3. Потребительская организация хочет сравнить износ определенного типа автомобильных шин, которые производятся заводами X и Y. Шины были установлены на различные автомобили. Каждый автомобиль имел или все X шины, или все Y шины. В данной модели на износ шин влияло только их качество. Результаты представлены в таблице.
| Номер машин | 2 | 3 | 4 | 5 | 6 | |
| Расстояние для X шин, тыс. км. | 50,1 | 47,0 | 48,6 | 48,8 | 50,2 | 48,0 |
| Расстояние для Y шин, тыс. км. | 53,9 | 50,3 | 48,5 | 51,3 | 49,7 | 51,0 |
Имеется ли основание предполагать, что два выпуска шин имеет разную износоустойчивость?
Задача 4. Потребительская организация хочет сравнить износ определенного типа автомобильных шин, которые производятся заводами X и Y. Шины были установлены на различные автомобили. Каждый автомобиль имел или все X шины, или все Y шины. В данной модели на износ шин влияло только их качество. Результаты представлены в таблице.
| Номер машин | 2 | 3 | 4 | 5 | 6 | |
| Расстояние для X шин, тыс. км. | 50,1 | 47,0 | 48,6 | 48,8 | 50,2 | 48,0 |
| Расстояние для Y шин, тыс. км. | 53,9 | 50,3 | 48,5 | 51,3 | 49,7 | 51,0 |
Имеется ли основание предполагать, что два выпуска шин имеет разную износоустойчивость?
Задача 5. Для участия в обучающей игре по знанию английского языка учащиеся 8-х классов были разбиты на две группы из 11 и 12 человек. Согласно требованию игры, необходимо, чтобы дисперсия уровня подготовки по языку была в группах одинакова. Для проверки был проведен экспресс-тест знания языка, который показал следующие баллы. Оценить изменчивость знаний в двух группах
| Группа 1 | ||||||||||||
| Группа 2 |
Задача 6. На основании данных предыдущей задачи сопоставить уровень знаний в двух группах
Лабораторная работа № 6
Дисперсионный анализ
Цель работы:приобрести навыки исследования процессов и явлений с помощью средств табличного процессора MS Excel
Общие положения
Все факторы, характеризующие какой-либо процесс или явление в организации, делятся на две категории:
- зависимый фактор – фактор, который изучается (некий результат),
- независимые факторы – факторы, оказывающие влияние на результат.
Дисперсионный анализ применяется для оценки степени влияния выделенного набора независимых факторов на результат (зависимый фактор). Выводы о существенности влияния изучаемых факторов на результат проводятся путём сравнения частей общей дисперсии при выполнении требования нормальности распределения результативного признака.
По числу независимых факторов различают однофакторные и многофакторные дисперсионные модели. Модели с более чем одним независимым фактором дают возможность исследовать влияние на результат не только отдельных независимых факторов (главные влияния), но и их взаимодействия (наложения).
В среде MS Excel поддерживается три варианта дисперсионного анализа:
- однофакторный,
- двухфакторный с повторениями,
- двухфакторный без повторений.
