II. Анализ сезонных колебаний.

Таблица – Количество продукции, проданной в течение 13 кварталов

Номер квартала	Объем продаж, шт.

Необходимо проанализировать указанное множество данных и установить, можно ли обнаружить тенденцию. Если устойчивая тенденция действительно существует, данная модель может быть использована для прогнозирования количества проданной продукции в следующие кварталы.

На рис нанесены соответствующие значения. Как следует из графика, возможен возрастающий тренд, содержащий сезонные колебания. Объемы продаж в зимний период (1 и 4) значительно выше, чем в летний (2 и 3). Сезонная компонента практически не изменяется в течение трех лет. Этот факт свидетельствует в пользу модели с аддитивной компонентой.

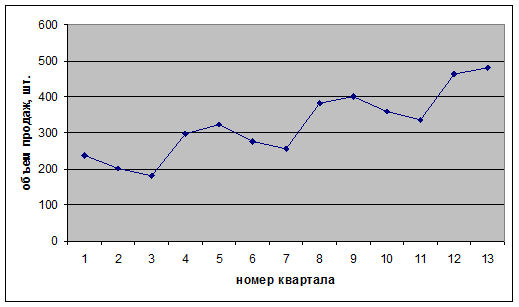
Рис. Объемы продаж компании по кварталам в
натуральном выражении

АНАЛИЗ МОДЕЛИ С АДДИТИВНОЙ КОМПОНЕНТОЙ:

А=Т+S+Е

где А – объем продаж,

Т – трендовое значение,

S – сезонная компонента,

Е – случайное значение (ошибка).

Моделью с аддитивной компонентой называется такая модель, в которой вариация значений переменной во времени наилучшим образом описывается через сложение отдельных компонент.

Для того чтобы элиминировать влияние сезонной компоненты, воспользуемся методом скользящей средней. Суть метода скользящей средней состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего. Просуммировав первые четыре значения, получим общий объем продаж в первом году. Если поделить эту сумму на четыре, можно найти средний объем продаж в каждом квартале первого года.

Полученное значение уже не содержит сезонной компоненты, поскольку представляет собой среднюю величину за год. Если последовательно передвигаться вперед, можно рассчитать средние квартальные значения. Данная процедура позволяет генерировать скользящие средние по четырем точкам для исходного множества данных. Получаемое таким образом множество скользящих средних представляет наилучшую оценку искомого тренда (см. табл.)

К сожалению, оценки значений тренда, полученные в результате расчета скользящих средних по четырем точкам, относятся к несколько иным моментам времени, чем фактические данные. Первая оценка, равная 229,8, представляет собой точку, совпадающую с серединой первого года, т.е. лежит в центре промежутка фактических значений объемов продаж во II и III кварталах. Вторая оценка, равная 251, лежит между фактическими значениями в III и IV кварталах. Для дальнейшего расчета требуются десезонализированные средние значения, соответствующие тем же интервалам времени, что и фактические значения за квартал. Положение десезонализированных средних во времени сдвигается путем дальнейшего расчета средних для каждой пары значений.

Номер квартала	Объем продаж, шт. А	Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты А-Т=S+E

Теперь полученные значения тренда можно использовать для нахождения оценок сезонной компоненты. Рассчитаем:

А – Т = S + E

Для каждого квартала проводится оценка сезонной компоненты, которые включают в себя ошибку или случайную величину. Прежде чем можно будет использовать сезонную компоненту, нужно пройти два следующих этапа. Необходимо найти средние значения сезонных оценок для каждого сезона года. Эта процедура позволит уменьшить некоторые значения ошибок. Наконец, скорректировать средние значения, увеличивая или уменьшая их на одно и то же число таким образом, чтобы общая их сумма была равна нулю. Это необходимо, чтобы усреднить значения сезонной компоненты в целом за год

Таблица – Расчет средних значений сезонной компоненты

	Год	Номер квартала
Первый
Второй
Третий
Оценка сезонной компоненты						Сумма
Скорректированная сезонная компонента						Сумма = 0

Аналогичная процедура применима при определении сезонной вариации за любой промежуток времени. Если, например, в качестве сезонов выступают дни недели, для элиминирования влияния ежедневной «сезонной компоненты» также рассчитывают скользящую среднюю, но уже не по четырем, а по семи точкам. Эта скользящая средняя представляет собой значение тренда в середине недели, т.е. в четверг; таким образом, необходимость в процедуре центрирования отпадает.

При анализе ряда динамики важное значение имеет выявление сезонных колебаний. При изучении сезонных колебаний используются специальные показатели – индексы сезонности ( ).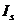

Для ряда внутригодовой динамики, в которой основная тенденция роста незначительна (или она не наблюдается совсем), изучение сезонности основано на методе постоянной средней:являющейся средней из всех рассматриваемых уровней. Самый простой способ заключается в следующем: для каждого года рассчитывается средний уровень, а затем с ним сопоставляется (в процентах) уровень каждого месяца. Это процентное отношение обычно именуется индексом сезонности:

.

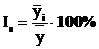Десезонализация исходных данных. Она заключается в вычитании соответствующих значений сезонной компоненты из фактических значений данных за каждый квартал, т.е. А - S = Т + Е, что показано ниже.

Таблица – Расчет десезонализированных данных

Номер квартала	Объем продаж, шт. А	Сезонная компонента, шт. S	Десезонализированный объем продаж, шт. А-S=Т+Е

Новые оценки значений тренда, которые еще содержат ошибку, можно использовать для построения модели основного тренда. Если нанести эти значения на исходную диаграмму, можно сделать вывод о существовании явного линейного тренда.

Наиболее эффективным способом выявления основной тенденции развития является (линия тренда) аналитическое выравнивание.

Для выравнивания ряда динамики по прямой (на основе линейной функции) используется уравнение:

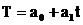
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров 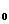a и a :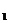

;

,

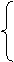
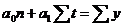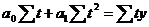где y – исходный уровень ряда динамики;

n –число членов ряда;

t – показатель времени, который обозначается порядковыми номерами, начиная от низшего.

Расчет ошибок или случайной компоненты. Модель имеет следующий вид:

А = Т + S + E

Вычитая значение сезонной компоненты и тренда из фактических объемов продаж, получим значения ошибок.

Таблица– Расчет ошибок для модели с аддитивной компонентой

Номер квартала	Объем продаж, шт. А	Сезонная компонента, шт. S	Трендовое значение, шт. Т	Ошибка, шт. А-S-T=E

Последний столбец этой таблицы можно использовать при расчете среднего линейного отклонения и дисперсии:

Л = ,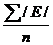

где Л – среднее линейное отклонение

n – количество данных.

,

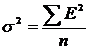где 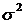– дисперсия.