Геометрический смысл частных производных функции двух переменных.
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_________________________________________________________________________________________ __________________________________________________________________________________________________________________________________________________________________________________
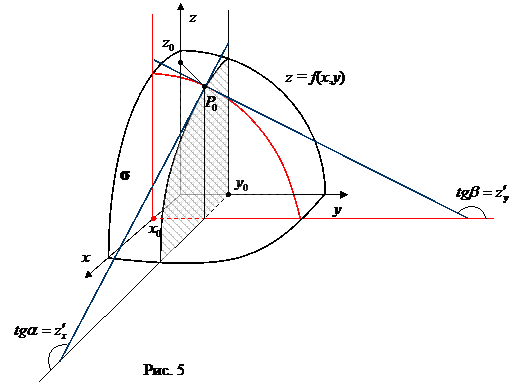
Частные производные высших порядков.
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Схема формирования частных производных высших порядков функции двух переменных.
 |
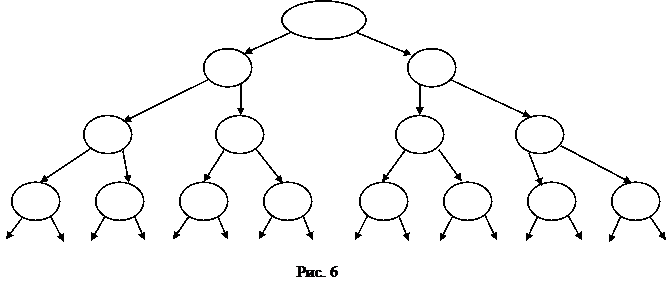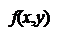
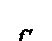
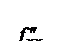
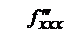
Определение. Смешанными частными производными называют___________________________
_________________________________________________________________________________________________________________________________________________________________________________
Теорема (о смешанных производных) ______________________________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Принимаем теорему без доказательств.
Пример.Найти частные производные второго порядка функции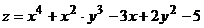 
.
Решение. Производную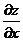 
найдём, считая х переменной, а у постоянной величиной:
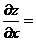
Производную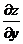 
найдём, считая у переменной, а х постоянной величиной:
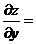
Вторые производные по х и по у будем искать, дифференцируя найденные производные первого порядка:
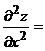
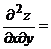
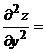
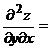
Мы убедились, что теорема выполняется:
Полный дифференциал функции.
По рис.4 _______________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________________
Определение функции, дифференцируемой в точке. _____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
(1)
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение полного дифференциала.___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
(2)
Примем без доказательств, что если функция z = f(x,y) дифференцируема в точке M(x;y), то 
и 
. Приращения 
, 
. Тогда равенство (2) можно переписать, как
Приложение полного дифференциала к приближённым вычислениям.
Линеаризация функции в окрестности точки.
Постановка задачи и вывод формулы.____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_________________________________________________________________________________________
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Пример.Вычислить приближенное значение функции 
в точке 
с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
Решение.______________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
§ 7. Экстремум функции двух переменных.
Окрестность точки______________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение максимума функции двух переменных_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение минимума функции двух переменных._________________ _______
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение экстремума._______________________________________________________ _______________________________________________________________________________________
Теорема (необходимое условие экстремума)__________________________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Принимаем без доказательств.
Необходимое условие экстремума не является достаточным (!)
Пример.Рассмотрим функцию 
(рис. 10).
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение критической (стационарной) точки второго рода ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Для ответа на вопрос, является ли точка области определения функции точкой экстремума, нужно использовать достаточное условие экстремума.
Теорема (достаточное условие экстремума)__________________________________________
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Пример 1.Исследовать на экстремум функцию 
.
Решение.
1) Находим производные первого порядка.
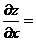
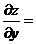
2) Находим критические точки. Для этого решим систему уравнений:
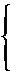
Получаем две критические точки: __________________
3) Находим производные второго порядка:
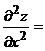
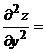
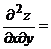
4) Исследуем первую критическую точку:
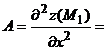
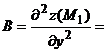
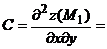
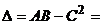
Следовательно, ________________________________________________
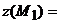
5) Исследуем вторую критическую точку:
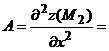
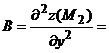
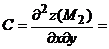
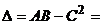
Следовательно, ________________________________________________
Пример 2.Исследовать на экстремум функцию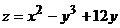 
.
Решение. (самостоятельно)
1) Находим производные первого порядка.
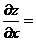
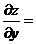
2) Находим критические точки. Для этого решим систему уравнений:
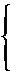
Получаем две критические точки: __________________
3) Находим производные второго порядка:
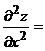
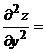
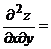
4) Исследуем первую критическую точку:
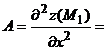
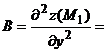
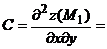
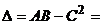
Следовательно, ________________________________________________
5) Исследуем вторую критическую точку:
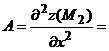
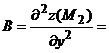
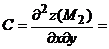
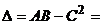
Следовательно, ________________________________________________
Наибольшее и наименьшее значение функции в замкнутой области. Глобальный экстремум.
Постановка задачи. ____________________________________________________________
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________