Интерпретация параметров моделей с распределенным лагом
Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна и равна p
yt=a+b0xt+b1xt-1+b2xt-2+…+bpxt-p+εt (6.6)
Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной в течение p следующих моментов времени. Коэффициент регрессии b0 при переменной xt характеризует среднее абсолютное изменение yt при изменении xt на одну единицу своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.
В момент (t + 1) совокупное воздействие факторной переменной xt на результат yt составит (b0+b1) усл. ед., в момент (t + 2) это воздействие можно охарактеризовать суммой (b0+b1+b2) и т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.
С учетом конечной величины лага можно сказать, что изменение переменной xt в момент t на 1 усл. ед. приведет к общему изменению результата через l моментов времени на (b0+b1+...+bl) абсолютных единиц.
Введем следующее обозначение:
b = b0+b1+...+bl. (6.7)
Величину b называют долгосрочным мультипликатором. Он показывает абсолютное изменение в долгосрочном периоде t + l результата под влиянием изменения на 1 ед. фактора х.
Применение обычного МНК к таким моделям в большинстве случаев затруднительно по следующим причинам.
Во-первых, текущие и лаговые значения независимой переменной, как правило, тесно связаны друг с другом. Тем самым оценка параметров модели проводится в условиях высокой мультиколлинеарности факторов. Во-вторых, при большой величине лага уменьшается число наблюдений, по которому строится модель, и увеличивается число ее факторных признаков. Это ведет к потере числа степеней свободы в модели. В-третьих, в моделях с распределенным лагом часто возникнет проблема автокорреляции остатков. Вышеуказанные обстоятельства приводят к значительной неопределенности относительно оценок параметров модели, снижению
их точности и получению неэффективных оценок. Чистое влияние факторов на результат в таких условиях выявить невозможно. Поэтому на практике параметры моделей с распределенным лагом проводят в предположении определенных ограничений на коэффициенты регрессии и в условиях выбранной структуры лага.
Рассмотрим теперь следующую модель авторегрессии:
yt=a+b0xt+c1yt-1+εt.
Как и в модели с распределенным лагом, b0 в этой модели характеризует краткосрочное изменение yt под воздействием изменения xt на 1 ед. Однако промежуточные и долгосрочный мультипликаторы в моделях авторегрессии несколько иные. К моменту времени (t + 1) результат yt изменился под воздействием изменения изучаемого фактора в момент времени t на величину b0, а yt+1 под воздействием своего изменения в непосредственно предшествующий момент времени на c1. Таким образом, общее абсолютное изменение результата в момент (t + 1) составит b0c1. Аналогично в момент времени (t + 2) абсолютное изменение результата составит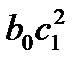 
и т.д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточных мультипликаторов
b = b0+b0c1+ +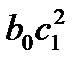 
...
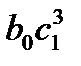С учетом предположения |c1| < 1 (называемое условие стабильности) последнее соотношение преобразуется к виду
b = b0(c1+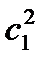 
+ 
...)= 
.
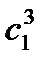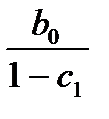Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.
6.6. Практический блок
Пример.
Дан временной ряд среднесписочной численности промышленно-производственного персонала промышленности Курской области, тыс. чел.
| Годы | |||||||||||||||||||
| y | 194,8 | 194,5 | 192,9 | 189,8 | 189,2 | 185,6 | 180,4 | 180,5 | 166,8 | 155,5 | 146,8 | 133,4 | 131,2 | 124,5 | 122,3 | 122,8 | 121,5 | 114,5 | 104,1 |
Задание:
1. Выбрать модель тренда с помощью диаграммы Excel.
2. Построить технологические таблицы по расчетным значениям и показателям адекватности модели.
3. Оценить устойчивость тенденции.
Параметры уравнения тренда могут быть найдены добавлением линии тренда в диаграмме Excel или решением системы уравнений по МНК.
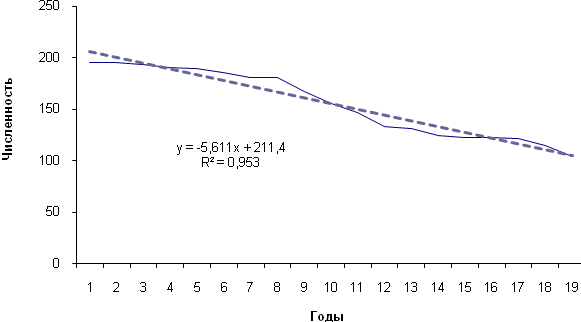
Рис.6.1 Аппроксимация линейной функцией
Рис.6.2 Аппроксимация параболической функцией
В случае использования уравнения прямой линии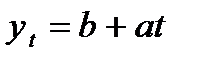
согласно МНК: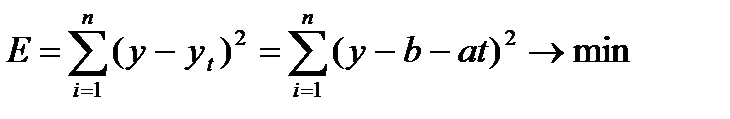 
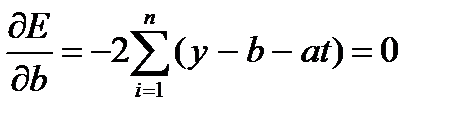
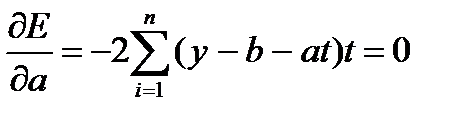
После преобразований получим систему:
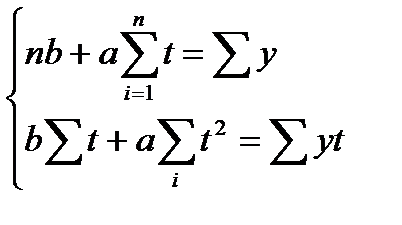
В случае использования уравнения параболы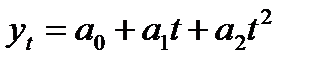 
согласно МНК:
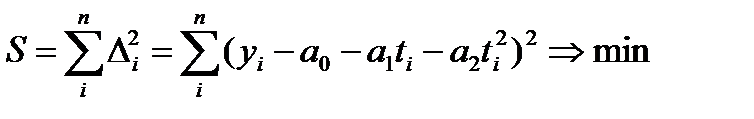
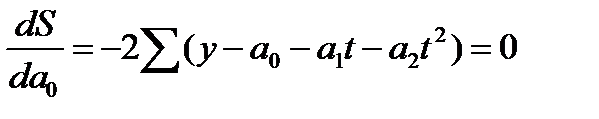
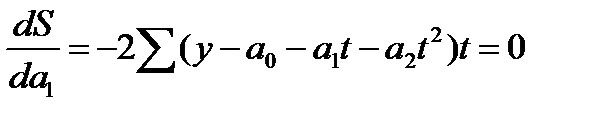
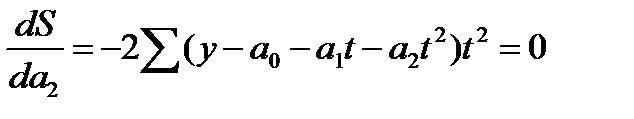
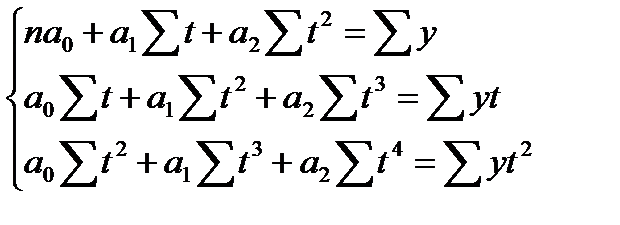
Для решения системы без ЭВМ и расчета показателей адекватности составляются технологические таблицы. Решение систем уравнений предполагает расчет необходимых сумм по фактическим данным.
Технологическая таблица расчета показателей
адекватности функции уt = b+at
| t | y | yt | y- yt | 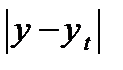 | 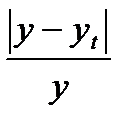 | (y- yt)2 |
| 194,8 | 205,828 | 11,028 | 11,028 | 0,057 | 121,619 | |
| 194,5 | 200,216 | 5,716 | 5,716 | 0,029 | 32,675 | |
| 192,9 | 194,604 | 1,704 | 1,704 | 0,009 | 2,905 | |
| 189,8 | 188,992 | -0,808 | 0,808 | 0,004 | 0,652 | |
| 189,2 | 183,381 | -5,820 | 5,820 | 0,031 | 33,867 | |
| 185,6 | 177,769 | -7,831 | 7,831 | 0,042 | 61,331 | |
| 180,4 | 172,157 | -8,243 | 8,243 | 0,046 | 67,952 | |
| 180,5 | 166,545 | -13,955 | 13,955 | 0,077 | 194,748 | |
| 166,8 | 160,933 | -5,867 | 5,867 | 0,035 | 34,423 | |
| 155,5 | 155,321 | -0,179 | 0,179 | 0,001 | 0,032 | |
| 146,8 | 149,709 | 2,909 | 2,909 | 0,020 | 8,463 | |
| 133,4 | 144,097 | 10,697 | 10,697 | 0,080 | 114,430 | |
| 131,2 | 138,485 | 7,285 | 7,285 | 0,056 | 53,076 | |
| 124,5 | 132,873 | 8,373 | 8,373 | 0,067 | 70,114 | |
| 122,3 | 127,262 | 4,962 | 4,962 | 0,041 | 24,616 | |
| 122,8 | 121,650 | -1,150 | 1,150 | 0,009 | 1,323 | |
| 121,5 | 116,038 | -5,462 | 5,462 | 0,045 | 29,837 | |
| 114,5 | 110,426 | -4,074 | 4,074 | 0,036 | 16,599 | |
| 104,1 | 104,814 | 0,714 | 0,714 | 0,007 | 0,510 | |
| Сумма | 0,692 | 869,170 |
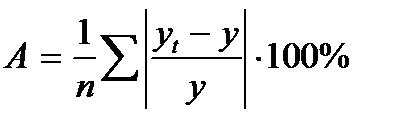- средняя ошибка аппроксимации
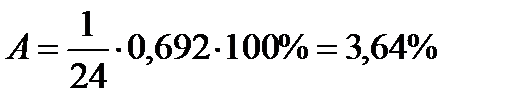
Стандартное отклонение:
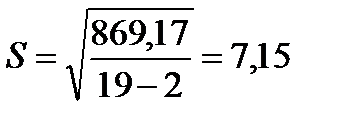
Технологическая таблица расчета показателей
адекватности функции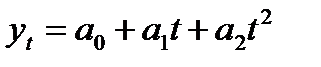 
| t | y | yt | y- yt | 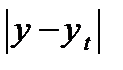| 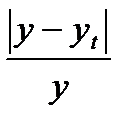| (y- yt)2 |
| 194,8 | 202,958 | 8,158 | 8,158 | 0,042 | 66,559 | |
| 194,5 | 198,304 | 3,804 | 3,804 | 0,020 | 14,472 | |
| 192,9 | 193,537 | 0,637 | 0,637 | 0,003 | 0,406 | |
| 189,8 | 188,658 | -1,142 | 1,142 | 0,006 | 1,304 | |
| 189,2 | 183,666 | -5,534 | 5,534 | 0,029 | 30,625 | |
| 185,6 | 178,561 | -7,039 | 7,039 | 0,038 | 49,542 | |
| 180,4 | 173,344 | -7,056 | 7,056 | 0,039 | 49,784 | |
| 180,5 | 168,014 | -12,486 | 12,486 | 0,069 | 155,890 | |
| 166,8 | 162,572 | -4,228 | 4,228 | 0,025 | 17,876 | |
| 155,5 | 157,017 | 1,517 | 1,517 | 0,010 | 2,301 | |
| 146,8 | 151,349 | 4,549 | 4,549 | 0,031 | 20,697 | |
| 133,4 | 145,569 | 12,169 | 12,169 | 0,091 | 148,089 | |
| 131,2 | 139,676 | 8,476 | 8,476 | 0,065 | 71,849 | |
| 124,5 | 133,671 | 9,171 | 9,171 | 0,074 | 84,107 | |
| 122,3 | 127,553 | 5,253 | 5,253 | 0,043 | 27,594 | |
| 122,8 | 121,322 | -1,478 | 1,478 | 0,012 | 2,183 | |
| 121,5 | 114,979 | -6,521 | 6,521 | 0,054 | 42,521 | |
| 114,5 | 108,523 | -5,977 | 5,977 | 0,052 | 35,720 | |
| 104,1 | 101,955 | -2,145 | 2,145 | 0,021 | 4,601 | |
| Сумма | 0,723 | 826,123 |
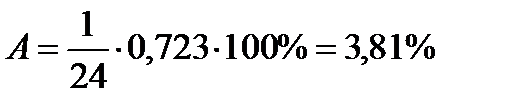
Стандартное отклонение: 
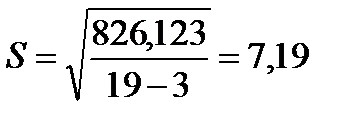
Сравним уравнения трендов по показателям адекватности.
| Уравнения трендов |  | |  |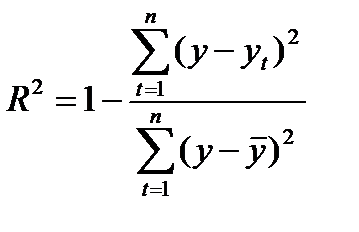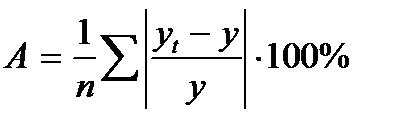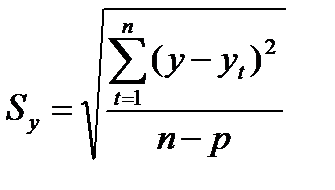
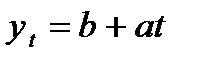 | 0,954 | 3,64% | 7,15 |
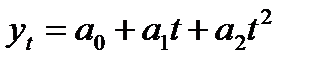| | 0,956 | 3,81% | 7,19 |
По показателям адекватности выбираем функцию уt = b+at, которую будем использовать для расчета показателей колеблемости и устойчивости.
Показатель колеблемости равен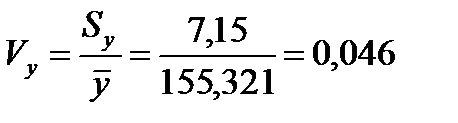 
Показатель устойчивости -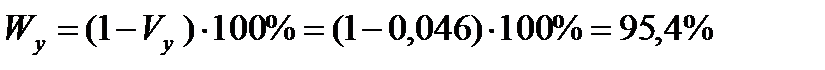 
Показатель устойчивости характеризует близость фактических уровней к тренду на 95,4%.
2.Для оценки устойчивости уровней временного ряда как процесса их направленного изменения рассчитаем коэффициент корреляции рангов Ч.Спирмэна:
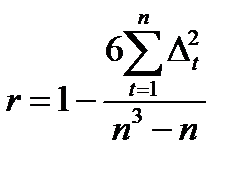, где
n – число уровней временного ряда;
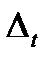- разность рангов уровней и номеров периодов времени.
| t | y | Ранг (y) |  |  |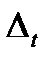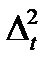
| 194,8 | ||||
| 194,5 | ||||
| 192,9 | ||||
| 189,8 | ||||
| 189,2 | ||||
| 185,6 | ||||
| 180,4 | ||||
| 180,5 | ||||
| 166,8 | ||||
| 155,5 | ||||
| 146,8 | -2 | |||
| 133,4 | -4 | |||
| 131,2 | -6 | |||
| 124,5 | -8 | |||
| 122,3 | -11 | |||
| 122,8 | -11 | |||
| 121,5 | -14 | |||
| 114,5 | -16 | |||
| 104,1 | -18 | |||
| Сумма |
Коэффициент Спирмена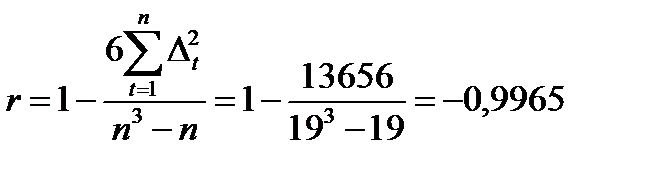 
, достаточно близок к -1, что доказывает устойчивость снижения показателей ряда.
Контрольные вопросы
1. Трендовые модели с независимыми значениями случайной составляющей.
2. Полиномиальный тренд.
3. Трендовые модели с сезонными колебаниями.
4. В чем суть метода экспоненциального сглаживания?
5. В чем заключается проблема автокорреляции остатков и как она проявляется?
6. В чем состоит специфика построения моделей регрессии по временным рядам данных?
7. Перечислите основные методы исключения тенденции. Сравните их преимущества и недостатки.
8. Изложите суть метода отклонений от тренда.
9. В чем сущность метода последовательных разностей?
10. Какова интерпретация параметра при факторе времени в моделях регрессии с включением фактора времени?
11. Охарактеризуйте понятие автокорреляции в остатках. Какими причинами может быть вызвана автокорреляция в остатках?
12. Что такое критерий Дарбина – Уотсона? Изложите алгоритм его применения для тестирования модели регрессии на автокорреляцию в остатках.
13. Перечислите основные этапы обобщенного МНК.
14. Приведите примеры экономических задач, эконометрическое моделирование которых требует применения моделей с распределенным лагом и моделей авторегрессии.
15. Какова интерпретация параметров модели с распределенным лагом?
16. Какова интерпретация параметров модели авторегрессии?
17. Изложите методику применения метода инструментальных переменных для оценки параметров модели авторегрессии.
18. Изложите методику тестирования модели авторегрессии на автокорреляцию в остатках.
Задания и задачи
1.Известны посезонные данные по объемам продаж сноубордов, шт. (y) в зависимости от цены, тыс.руб. (x). Построить линейную регрессионную модель с учетом сезонности.
| весна | лето | осень | зима | весна | лето | осень | зима | весна | лето | осень | зима | |
| y | ||||||||||||
| x | 4,5 | 6,5 | 5,5 | 5,5 | 3,5 |
2. Даны помесячные данные о печати фотографий в некоторой фирме. Построить линейную регрессионную модель с учетом сезонности.
| месяц | y, кол-во, шт. | x1, цена, руб. | x2, рекл., руб. | x3, праздники | x4, индекс цен | |
| январь, 2006 | 12 500 | 2,5 | ||||
| февраль | 7 600 | 0,99 | ||||
| март | 6 900 | 1,01 | ||||
| апрель | 13 500 | 1,01 | ||||
| май | 9 700 | 1,03 | ||||
| июнь | 10 700 | 1,04 | ||||
| июль | 12 100 | 1,05 | ||||
| август | 9 700 | 3,5 | 1,03 | |||
| сентябрь | 7 000 | 1,05 | ||||
| октябрь | 7 200 | 1,05 | ||||
| ноябрь | 8 200 | 1,06 | ||||
| декабрь | 8 400 | 1,1 | ||||
| январь, 2007 | 13 100 | 1,11 | ||||
| февраль | 8 700 | 1,12 | ||||
| март | 12 200 | 1,14 | ||||
| апрель | 6 900 | 1,16 | ||||
| май | 6 200 | 1,17 | ||||
| июнь | 9 600 | 1,19 | ||||
| июль | 8 700 | 1,18 | ||||
| август | 11 900 | 1,18 | ||||
| сентябрь | 12 600 | 1,2 | ||||
| октябрь | 7 900 | 1,22 | ||||
| ноябрь | 9 300 | 1,24 | ||||
| декабрь | 11 800 | 1,27 |
3. Объем продаж мороженого (млн.шт.) за 5 лет в зависимости от цены (руб.) и сезона.
| год | сезон | y, кол-во | цена | индекс цен | x, цена инд. | z(1), весна | z(2), лето | z(3), осень |
| весна | 1,5 | 3,00 | ||||||
| лето | 2,6 | 1,11 | 3,60 | |||||
| осень | 1,7 | 3,5 | 1,15 | 3,04 | ||||
| зима | 0,9 | 3,5 | 1,26 | 2,78 | ||||
| весна | 1,4 | 1,34 | 2,99 | |||||
| лето | 1,40 | 2,86 | ||||||
| осень | 2,8 | 1,45 | 2,76 | |||||
| зима | 1,6 | 1,52 | 2,63 | |||||
| весна | 1,9 | 4,5 | 1,59 | 2,83 | ||||
| лето | 3,2 | 1,63 | 3,07 | |||||
| осень | 2,7 | 4,5 | 1,68 | 2,68 | ||||
| зима | 4,5 | 1,78 | 2,53 | |||||
| весна | 2,2 | 1,87 | 2,67 | |||||
| лето | 3,4 | 1,95 | 2,56 | |||||
| осень | 2,6 | 2,01 | 2,49 | |||||
| зима | 2,1 | 2,09 | 2,39 | |||||
| весна | 2,9 | 2,16 | 2,31 | |||||
| лето | 3,3 | 2.19 | 2,74 | |||||
| осень | 2,5 | 2,24 | 2,68 | |||||
| зима | 2,2 | 2,32 | 2,59 |
Задание:
Выбрать лучший тренд и пояснить экономический смысл его параметров.
Рассчитать частные коэффициенты эластичности.
Сделать вывод о силе связи результата и факторов.
Определить парные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
Дать оценку полученного уравнения на основе коэффициента детерминации.
Сделать прогноз по объемам продаж мороженого на 2010г.
Тесты
1. Какие точки исключаются из временного ряда процедурой сглаживания?
a) стоящие в начале временного ряда,
б) стоящие в конце временного ряда,
в) стоящие и в начале, и в конце временного ряда.
2. Какое количество точек предпочтительнее брать для расчёта сглаженного значения?
a) чётное,
б) нечётное,
в) любое.
3. Какие временные ряды называются интервальными?
a) уровни которых характеризуют изучаемое явление за определённые интервалы времени,
б) уровни которых отражают величину изучаемого явления на определённый момент времени,
в) уровни которых характеризуют изучаемое явление с помощью средних или относительных величин.
4.Какие временные ряды называются моментными?
a) уровни которых характеризуют изучаемое явление за определённые интервалы времени,
б) уровни которых отражают величину изучаемого явления на определённый момент времени,
в) уровни которых характеризуют изучаемое явление с помощью средних или относительных величин.
5.От чего зависит количество точек, исключаемых в результате сглаживания?
a) от применяемого метода сглаживания,
б) от количества точек, используемых при вычислении сглаженного значения,
в) от длины временного ряда.
6.Почему в процедурах удобно использовать нечётное количество точек?
a) в случае нечётного количества из временного ряда исключается меньшее количество точек,
б) при нечётном количестве есть центральная точка, которая заменяется сглаженным значением,
в) эффективность сглаживания повышается.
7. Какая функция используется при моделировании показателей с постоянным ростом?
a) линейная,
б) показательная,
в) степенная.
8.В каком случае рекомендуется применять для моделирования показателей с увеличивающимся ростом параболу?
a) если относительная величина прироста увеличивается неограниченно,
б) если абсолютная величина прироста растёт по линейному закону,
в) если относительная величина прироста неизменна.
9. При сглаживании временного ряда с помощью 7-членной скользящей средней теряются
a) первые и последние 3 значения временного ряда,
б) первые и последние 7 значений временного ряда,
в) только первые 3 значения,
г) только первые 7 значений.
10.При использовании взвешенной скользящей средней весовые коэффициенты при сглаживании по полиному второго порядка будут такими же, как при сглаживании
a) по полиному 3-го порядка,
б) по полиному 1-го порядка,
в) по полиному 4-го порядка.
11. Если значения цепных абсолютных приростов временного ряда примерно одинаковы, то для вычисления прогнозного значения в следующей точке корректно использовать
a) средний абсолютный прирост,
б) средний темп роста,
в) средний темп прироста.
12. Для оценки коэффициента автокорреляции используются:
а) процедура Дарбина,
б) процедура Кохрана-Оркатта,
в) процедура Хилдреда-Лу.
13. Модель спроса–предложения выражается:
а) трендовой моделью;
б) системой одновременных уравнений;
в) регрессионным уравнением;
г) тренд-сезонной моделью.
14. Какие методы позволяют выявить наличие тенденции в ряду динамики:
а) критерий Стьюдента;
б) метод экспоненциального сглаживания;
в) критерий Кендела;
г) критерий Фишера.
15. Ряд динамики был сглажен скользящей средней 4-го порядка с последующим центрированием. Какому уровню ряда соответствует первое центрированное значение:
а) первому;
б) второму;
в) третьему;
г) четвертому.
16. При построении аддитивной тренд-сезонной модели средние индексы сезонности рассчитываются как средние за одноименные периоды значения:
а) разностей фактических и сглаженных значений временного ряда;
б) частного от деления фактических значений на сглаженные значения временного ряда;
в) разностей фактических и среднего значения временного ряда;
г) частного от деления фактических значений на среднее значение временного ряда.
17. Для аддитивной тренд-сезонной модели не верно утверждение, что
а) амплитуда колебаний со временем не меняется;
б) амплитуда колебаний со временем убывает;
в) сумма скорректированных индексов сезонности равна 0;
г) сумма скорректированных индексов сезонности равна 4.
6.7. Самостоятельная работа студентов
Литература для самостоятельной работы
1. Эконометрика: Учебник./ Под ред. И.И. Елисеевой. – 2-е изд.– М.: Финансы и статистика, 2005. – 276 с.
2. Практикум по эконометрике. Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2005.
3. Мхитарян В.С., Архипова М.Ю., Сиротин В.П. Эконометрика: Учебно-методический комплекс. – М.: Изд. центр ЕАОИ. 2008. – 144 с.
4. Дубров А.М., Мхитарян В.С., Трошин Л.И. Математическая статистика для бизнесменов и менеджеров. – М.: МЭСИ, 2004. – 140 с.
5. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс, 3-е изд. – М.: Дело, 2005. – 503 с.
6. Мхитарян В.С., Трошин Л.И. Исследование зависимостей методами корреляции и регрессии. – М.: МЭСИ, 2004. – 51 с.
7. Айвазян С.А., Мхитарян В.С. Практикум по прикладной статистике и эконометрике. – М.: МЭСИ, 2003.
INTERNET-ресурсы
1. http://upereslavl.botik.ru/UP/ECON/econometrics/top1/tsld006.htm
2. http://www.nsu.ru/ef/tsy/ecmr/study.htm
3. http://www.nsu.ru/ef/tsy/ecmr/index.htm
4. http://www.statsoft.ru/home/textbook/def ault.htm
5. http://www.nsu.ru/ef/tsy/ecmr/study.htm
6. http://www.dataforce.net/~antl/article/econometric
7. http://www.nsu.ru/ef/tsy/ecmr/study.htm
8. http://www.tvp.ru/vnizd/mathem4.htm
9. http://www.kgtu.runnet.ru/WD/TUTOR/textbook/modules/stmulreg.html
10. http://www.shpargalka.ru/statis.ru/doc/shpr_e31.htm
11. http://www3.unicor.ac.ru/d024/p011993.htm
12. http://www.gauss.ru/educat/systemat/butenkov/.asp
13. http://crow.academy.ru/econometrics/seminars_/sem_08_/sem_08.htm
14. http://crow.academy.ru/econometrics/lectures_/lect_03_/index.htm