Обобщенный метод наименьших квадратов.Метод Главных Компонент.
При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов (метод OLD – OrdinaryLeastSquares) заменять обобщенным методомGLS(GeneralizedLeastSquares). Он применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии.
Суть метода заключается в том, что подбираются коэффициенты Кi, такие, что σ2ei =σ2 ·Кi,
где σ2ei – дисперсия ошибки при конкретном i–ом значении фактора;
σ2 – постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
Кi– коэффициент пропорциональности, меняющийся с изменением величины фактора.
Уравнение парной регрессии при этом принимает вид
уi/ 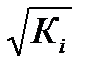 = a0/
= a0/ 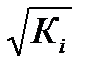 + a1хi/
+ a1хi/ 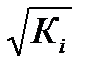 +ei.
+ei.
По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляют собой взвешенную регрессию, в которой переменные у и х взяты с весами 1/ 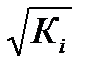 . Аналогичный подход применяют и для множественной регрессии, уравнение с преобразованными переменными принимает вид
. Аналогичный подход применяют и для множественной регрессии, уравнение с преобразованными переменными принимает вид
у/ 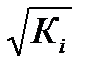 =a0/
=a0/ 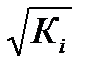 +a1х1/
+a1х1/ 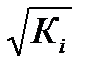 +a2х2/
+a2х2/ 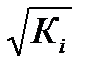 +…+amхm/
+…+amхm/ 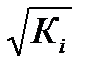 +e. (5.1)
+e. (5.1)
Параметры такой модели зависят от концепции, принятой для коэффициента пропорциональности К. В эконометрических исследованиях довольно часто выдвигается гипотеза, что остатки ei пропорциональны значениям фактора. Пусть, например, у – издержки производства, х1 – объем продукции, х2 – основные производственные фонды, х3 – численность работников, тогда уравнение у =a0 +a1х1 +a2х2 + a3х3 +e является моделью издержек производства с объемными факторами. Предполагая, что σ2ei пропорциональна квадрату численности работников (т.е. 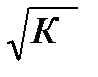 = х3), получим в качестве результативного признака затраты на одного работника (у/х3), а в качестве факторов производительность труда (х1/х3) и фондовооруженность труда (х2/х3). Соответственно трансформированная модель примет вид
= х3), получим в качестве результативного признака затраты на одного работника (у/х3), а в качестве факторов производительность труда (х1/х3) и фондовооруженность труда (х2/х3). Соответственно трансформированная модель примет вид
у/ х3 =a3 +a1х1/ х3 +a2х2/ х3 +e,
где вычисленные параметры a3, a1, a2 численно не совпадают с аналогичными параметрами предыдущей модели. Кроме того, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее изменение издержек производства с изменением абсолютного значения соответствующего фактора на единицу, они фиксируют теперь среднее изменение затрат на работника в зависимости от изменения производительности труда на единицу; и в зависимости от изменения фондовооруженности труда на единицу.
Если же предположить, что в первоначальной модели дисперсия остатков пропорциональна квадрату объема продукции, получаем уравнение регрессии
у/ х1 =a1 +a2х2/ х1 +a3х3/ х1 +e,
где у/ х1 – затраты на единицу продукции, х2/ х1 – фондоемкость продукции, х3/х1 – трудоемкость продукции.
Переход к относительным величинам существенно снижает вариацию фактора и соответственно уменьшает дисперсию ошибки.
Метод Главных Компонент (PrincipalComponentsAnalysis, PCA) – один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном в 1901 г. Он применяется для:
1) наглядного представления данных;
2) обеспечения лаконизма моделей, упрощения счета и интерпретации;
3) сжатия объемов хранимой информации.
Метод обеспечивает максимальную информативность и минимальное искажение геометрической структуры исходных данных. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных. Иногда метод главных компонент называют преобразованием Кархунена-Лоэва или преобразованием Хотеллинга. Другие способы уменьшения размерности данных – это метод независимых компонент, многомерное шкалирование, а также многочисленные нелинейные обобщения: метод главных кривых и многообразий, поиск наилучшей проекции, нейросетевые методы «узкого горла», самоорганизующиеся карты Кохонена и др.
Задача анализа главных компонент, имеет, как минимум, четыре базовых версии:
- аппроксимировать данные линейными многообразиями меньшей размерности;
- найти подпространства меньшей размерности, в ортогональной проекции на которые разброс данных (т.е. среднеквадратичное уклонение от среднего значения) максимален;
- найти подпространства меньшей размерности, в ортогональной проекции на которые среднеквадратичное расстояние между точками максимально;
- для данной многомерной случайной величины построить такое ортогональное преобразование координат, что в результате корреляции между отдельными координатами обратятся в ноль. Подробнее о методе главных компонент см. [9,10].
