Гиперболическая и логарифмическая регрессии. Полиномиальная и кусочно-полиномиальная регрессия.

Гиперболическая модель линеаризуется непосредственной заменой переменной y=1/y:

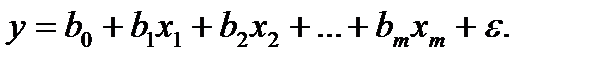
Эти функции используются при построении кривых Энгеля, которые описывают зависимость спроса на определенный вид товаров или услуг от уровня доходов потребителей или от цены товара.

Для определения однофакторной криволинейной функции регрессии по расположению точек на диаграмме рассеяния делают заключение о примерном виде этой функции, при этом необходимо учитывать особенности конкретной экономической задачи, в рамках которой анализируется взаимосвязь признаков.

Гиперболическая однофакторная регрессия имеет вид

у=b+а/х. (4.5)

Она может быть использована для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы х и процентом прироста заработной платы у. Английский экономист А.В.Филлипс, анализируя данные более чем за 100-летний период, в конце 50-х годов 20 века, установил обратную зависимость прироста заработной платы от уровня безработицы.

Выполнив замену 1/х = z, получаем линейную регрессию у=b+аz, параметры которой на компьютере (в Excel) можно вычислить с помощью функции ЛИНЕЙН.

Модели вида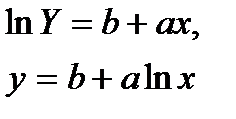

называются полулогарифмическими однофакторными моделями. Эти модели также относятся к нелинейным моделям относительно включенных в анализ объясняющих переменных, но линейным по параметрам.

Такие модели обычно используются в тех случаях, когда необходимо определять темп роста или прироста каких-либо экономических показателей. Например, при анализе банковского вклада по первоначальному вкладу и процентной ставке, при исследовании зависимости прироста объема выпуска от относительного (процентного) увеличения затрат ресурса, бюджетного дефицита от темпа роста ВНП, темпа роста инфляции от объема денежной массы и т.д.

Зависимость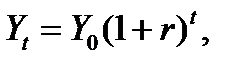

где Y₀ – начальная величина переменной Y (например, первоначальный вклад в банке); r – сложный темп прироста величины Y (процентная ставка); Y_t– значение величины Y в момент времени t (вклад в банке в момент времени t). Эта модель легко сводится к полулогарифмической первого вида, параметры которой легко оцениваются с помощью МНК.

Полиномиальная регрессия имеет вид

у=a₀+a₁х +a₂х² +…+a_mх^m. (4.6)

Если для разных интервалов значений фактора х применяется полиномиальная регрессия с разными степенями m, то имеет место кусочно-полиномиальная регрессия. Неизвестные параметры уравнения криволинейной регрессии также находятся методом наименьших квадратов.

Например, глядя на рис.2.1 (см. пример 2.2), можно предположить, что имеет место параболическая регрессия второго порядка, т.е. следует искать уравнение регрессии вида

у_х= a₀+a₁х +a₂х² ,

где a₀, a₁, a₂ – неизвестные коэффициенты.

Пользуясь методом наименьших квадратов, получаем систему линейных уравнений относительно неизвестных параметров:

х⁴a₂+х³a₁+х²a₀=ух²,

х³a₂+х²a₁+хa₀ =ух, (4.7)

х²a₂+хa₁+a₀= у.

Пример4.1. По данным корреляционной таблицы 2.2 построить параболическую функцию регрессии.

Подставляя данные в (4.7), получаем систему:

286000a₂+11160a₁+460a₀=8100,

11160a₂+460a₁+20.4a₀=354,

460a₂+20.4a₁+a₀=17.4.

Решив эту систему, найдем a₂=0.055, a₁= – 2.26, a₀=38.2.

Искомое параболическое уравнение регрессии принимает вид:

у_х =0.055х² – 2.26х+38.2 (Пунктирная линия на рис. 2.1).

Легко убедиться, что условные средние, вычисленные по данному уравнению, незначительно отличаются от условных средних корреляционной таблицы.

у₁₀ =0.055×10² – 2.26×10+38.2=21.1,

у₂₀ =0.055×20² – 2.26×20+38.2=15,

у₃₀ =0.055×30² – 2.26×30+38.2=19.9.

Найденное уравнение хорошо согласуется с данными наблюдений.