Оценка и интерпретация параметров.
Для анализа статистической значимости полученных коэффициентов множественной линейной регрессии оценивают дисперсию D(ai) и стандартные отклонения S(ai)=ÖD(ai) коэффициентов ai. Аналогично (10) величина t=ai/S(ai), называемая t–статистикой, имеет распределение Стьюдента с (n-m-1) степенями свободы. Если число степеней свободы достаточно велико (не менее 10), то при 5%-ном уровне значимости можно приближенно считать оценку незначимой, если t–статистика по модулю меньше 1, и весьма надежной, если модуль t–статистики больше 3.
Коэффициенты множественной линейной регрессии ai имеют большой экономический смысл. Они показывают, на сколько изменится анализируемый показатель Y при изменении фактора Хi на единицу.
Пример 3.1. Рассмотрим аналитические модели спроса, используя ниже приведенные в табл.3.1 конкретные статистические данные обследования семей, сведенные в девять групп (с примерно одинаковым объемом потребления).
Таблица 3.1
| № группы | Расход на питание (у) | Душевой доход (х1) | Размер семей (х2) | ŷ | ej | ej2 |
| 1,5 | 333,6 | 99,4 | 9880,36 | |||
| 2,1 | 626,5 | –10,5 | 110,25 | |||
| 2,7 | 928,5 | –28,5 | 812,25 | |||
| 3,2 | 1189,8 | –76,8 | 5898,24 | |||
| 3,4 | 1340,5 | –34,5 | 1190,25 | |||
| 3,6 | 1493,6 | –5,6 | 31,36 | |||
| 3,7 | ||||||
| 4,0 | 1879,1 | 34,9 | ||||
| 3,7 | 2409,5 | 1,5 | 2,25 | |||
| Средние | 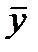 =1313,9 =1313,9 | 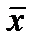 1 =6080,5 1 =6080,5 | 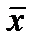 2 =3,1 2 =3,1 | 2198,2 |
Рассмотрим сначала однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода (х1)
ŷ =а0 + а1х1,
параметры которой а0 и а1 находятся по формулам (2.5), используя данные табл.3.1 и 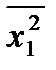 =(∑х12)/9=63989644,1,
=(∑х12)/9=63989644,1, 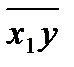 =(∑х1у)/9)=10894351. Решение: а0=660,06; а1 = 0,1075. Получаем уравнение регрессии ŷ =660,06 + 0,1075х1.
=(∑х1у)/9)=10894351. Решение: а0=660,06; а1 = 0,1075. Получаем уравнение регрессии ŷ =660,06 + 0,1075х1.
Затем вычисляются средняя квадратическая ошибка выборки (корень квадратный из дисперсии у)
Sу=√(∑(у – у)2)/n,
средняя квадратическая ошибка уравнения (2.3) Sŷ =√(∑(у – ŷ)2)/n и коэффициент детерминации Rŷх1 =√1 – Sŷ2/ Sу2.
В нашем примере Sу2=454070, Sŷ2=63846, следовательно
Rŷх1 =√1 – 63846/454070 =0,927.
Полученное значение свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.
Величина R2ŷх1показывает долю изменения результативного признака под воздействием факторного признака. В нашем примере R2ŷх1 =0,859; это означает, что фактором душевого дохода можно объяснить почти 86% изменения расходов на питание.
Рассмотрим теперь двухфакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода (х1) и размера семьи (х2)
ŷ =а0 + а1х1+ а2х2 .
Параметры модели а0 , а1и а2 находятся посредством решения следующей системы нормальных уравнений:
а0 + х1а1 + х2а2 = у
х1а0 + 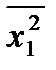 а1 + х1х2 а2 = ух1
а1 + х1х2 а2 = ух1
х2а0 + х1х2 а1+ 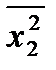 а2 = ух2,
а2 = ух2,
которая также формируется с применением метода наименьших квадратов (средние величины х1х2 , 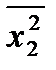 и ух2вычисляются аналогично однофакторной модели). Получаем систему
и ух2вычисляются аналогично однофакторной модели). Получаем систему
а0 + 6080,5а1 + 3,1а2 = 1313,9
6080,5а0 + 63989644,1а1 + 21649,1а2 = 10894351
3,1а0 + 21649,1а1 + 10,2а2 = 4488,
которую решаем, например, методом Гаусса.
Делим второе и третье уравнения на коэффициент при а0.
а0 + 6080,5а1 + 3,1а2 = 1313,9
а0 + 10523,75а1 + 3,56а2 = 1791,69
а0 + 6983,58а1 + 3,29а2 = 1447,74.
От второго и третьего уравнения отнимаем первое
а0 + 6080,5а1 + 3,1а2 = 1313,9
4443,25а1 + 0,46а2 = 477,79
903,08а1+ 0,19а2 = 133,84.
Делим второе и третье уравнения на коэффициент при а1.
а0 + 6080,5а1 + 3,1а2 = 1313,9
а1 + 0,0001035а2 = 0,1075316
а1+ 0,0002104а2 = 0,1482039.
От третьего уравнения отнимаем второе
а0 + 6080,5а1 + 3,1а2 = 1313,9
а1 + 0,0001035а2 = 0,1075316
0,0001069а2= 0,0406723.
Из третьего уравнения находим а2 =380.47; подставляя его во второе уравнение получаем а1 = 0,06815; подставляя найденные а1и а2 в первое уравнение, получаем а0 = –279.94; следовательно
ŷ = –279.94 + 0.06815х1+ 380.47х2 .
Для определения тесноты связи предварительно вычисляются теоретические значения ŷ, затем уклонения ej и их квадраты (колонки 5,6,7 табл.3.1). Получим Sŷ2 =(∑(у – ŷ)2)/n =2198,2. Используя ранее вычисленное Sу2=454070, получим R2 =1 – Sŷ2/ Sу2 =0,995. R2 показывает долю вариации результативного признака под воздействием изучаемых факторных признаков. У нас R2=0,995; это означает, что совместное влияние душевого дохода и размера семей объясняет почти 99,5% изменения расходов на питание.
