Измерение и интерпретация случайной составляющей.
Надежность получаемых оценок a0 и a1 зависит от дисперсии отклонений переменной у от оцененной линии регрессии ei = уi– aхi - b. Несмещенная оценка дисперсии случайной составляющей вычисляется по формуле
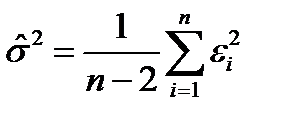 , (2.7)
, (2.7)
и является мерой разброса зависимой переменной вокруг линии регрессии (необъясненная дисперсия).
В качестве меры того, насколько хорошо регрессия описывает данную систему наблюдений, служит коэффициент детерминации, при этом вычисляются следующие суммы квадратов отклонений:
S2=åi(yi– 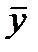 )2 – фактических значений от их среднего арифметического;
)2 – фактических значений от их среднего арифметического;
Ŝ2= åi (ŷi– 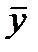 )2 – выровненных значений от среднего арифметического
)2 – выровненных значений от среднего арифметического
фактических значений;
Š2= åi (yi – ŷ i)2 – фактических от выровненных значений.
Имеет место равенство S2= Ŝ2 + Š2.
Коэффициент детерминации есть отношение объясненной части вариации ко всей вариации в целом
R2=Ŝ2/S2=1 – Š2/S2. (2.8)
Таким образом, чем «ближе» этот коэффициент к единице, тем лучше описание, разумеется, если при этом модель методически правильна.
В столбцах 8 и 10 табл.2.1 вычислены выровненные значения эмпирической функции регрессии и квадраты их отклонений от наблюденных значений.
В соответствии с (2.7) получаем оценку дисперсии случайной составляющей
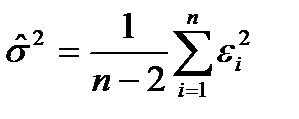 =0,0479/6=0,008.
=0,0479/6=0,008.
В соответствии с (2.8) значение коэффициента детерминации
R2= 1 – Š2/S2 = 1 – 0,0479/1,66=0,971
показывает, что 97,1% общей вариабельности розничного товарооборота объясняется изменениями числа работников, в то время как на все остальные факторы приходится лишь 2,9% вариабельности.
Найденные отклонения фактических значений от выровненных (столбец 9) позволяют провести сравнительный анализ работы различных магазинов. Прежде всего, необходимо обратить внимание на магазины с отрицательным отклонением (3, 4, 6). Особенно велико отклонение у 4-го магазина. Необходимо внимательно обследовать эти магазины и установить причины отклонений. Это может быть расположение магазина в стороне от основных потоков покупателей, плохое обслуживание, неудовлетворительный кадровый состав и т.п. Здесь, по-видимому, имеются резервы в организации труда работников. Напротив, в магазинах 1, 2, 5, 7 и 8 работники используются эффективнее статистического «норматива», но может оказаться, что эти магазины объективно находятся в лучших условиях.
Обозначим Sx=åi(xi – 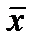 )2, тогда дисперсия параметра a1 вычисляется по формуле D(a1)=σ2/ Sx.
)2, тогда дисперсия параметра a1 вычисляется по формуле D(a1)=σ2/ Sx.
Значимость оцененного коэффициента регрессии a1 может быть проверена с помощью анализа его отношения к своему стандартному отклонению
t=a1/ÖD(a1). (2.9)
Эта величина имеет распределение Стьюдента с (n – 2) степенями свободы и называется t-статистика. (см. приложение 1). Можно использовать следующее грубое правило для оценки значимости коэффициента линейной регрессии:
- если t<1, то он не может быть признан значимым, поскольку доверительная вероятность здесь составляет менее 0,7;
- если 1<t<2, то сделанная оценка может рассматриваться как более или менее значимая, доверительная вероятность здесь примерно от 0,7 до 0,95;
- значение 2<t<3, свидетельствует о весьма значимой связи (доверительная вероятность от 0,95 до 0,99);
- t>3 есть практически стопроцентное свидетельство ее наличия.
Сформулированными правилами можно надежно пользоваться при n³10.
При большом размере выборки повторяющиеся пары наблюдений группируются в виде корреляционной таблицы. Если nyx–количество наблюдений одинаковых пар (х,у), то для вычисления коэффициента корреляции в формуле (2.1) необходимо брать ху=ånyxxiyi/n.
Для оценки тесноты любой корреляционной связи вводится корреляционное отношение Y к Х как отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:
hyx=sYx/sy. (2.10)
Здесь sYx=√(Snx(yx – y)2)/n,
sy= √Sny(y – y)2)/n,
где n – объем выборки (сумма всех частот); nx – частота значения х признака Х; ny – частота значения у признака Y; y – общая средняя признака Y;yx– условная средняя признака Y.
Чем ближе корреляционное отношение к 1, тем теснее связь между признаками, однако, оно не задает вида этой связи и не позволяет судить о степени близости наблюдений к какой-либо кривой.
Пример2.2. Пусть имеется распределение 50 га пахотной земли по количеству внесенных удобрений х (ц на 1 га) и по урожайности у (ц с 1 га), приведенное в табл. 2.2. В этой таблице, например, число 4, стоящее на пересечении 1-й строки и 1-го столбца, показывает, что на 4 га из 50 было внесено по 10 ц удобрений и при этом получена урожайность по 15 ц с га. Найти уравнение прямой линии регрессии Y на Х, коэффициент корреляции и корреляционное отношение по данным корреляционной табл. 2.2.
Таблица 2.2
| у | х | |||
| ny | ||||
| – | ||||
| nх | n =50 | |||
| ух |
Вычислим сначала все средние и дисперсии:
у=(38×15+12×25)/50=17.4,
х=(10×10+28×20+12×30)/50=20.4,
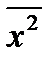 =(10×100+28×400+12×900)/50=460,
=(10×100+28×400+12×900)/50=460,
ху=(4×10×15+28×20×15+6×30×15+6×10×25+6×30×25)/50=354,
sх = Ö 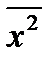 – (
– ( 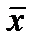 )2 =Ö460 – 20.42 =Ö43.84=6.62,
)2 =Ö460 – 20.42 =Ö43.84=6.62,
sy =Ö(38× (15 – 17.4)2 +12× (25 – 17.4)2)/50=4.27,
sYx =Ö(10× (21 – 17.4)2+28× (15 – 17.4)2+12× (20 – 17.4)2)/50=Ö7.44=2.73.
Тогда коэффициент корреляции из (2.2)
ryx =(354 – 20.4×17.4)/(6.62×4.27)= – 0.034,
коэффициент регрессии из (2.6)
ryx = –0.034×4.27/6.62= –0.022,
уравнение прямой регрессии имеет вид
ух – 17.4= –0.022(х – 20.4) или ух = –0.022х + 17.85
и корреляционное отношение из (2.10)
hyx=2.73/4.27=0.64.
Из вычисленных показателей можно сделать следующий вывод:
Линейной связи между признаками нет, но какая-то связь есть, причем весьма существенная. Диаграмма рассеяния и прямая линия регрессии построены на рис.2.1. (В кружках проставленыnyx).
ух = -0.022х+17.85
10 20 30
Рис.2.1. Диаграмма рассеяния (пример 2.2).
2.7. Практический блок
Примеры
1. Оценить линейную регрессию, построить график, найти коэффициент корреляции, стандартные ошибки коэффициентов регрессии, дать интерпретацию уравнению регрессии и коэффициентов корреляции.
А)
| x | 1351.7 | 1369.3 | 1479.1 | 1682.5 | 1799.0 | 1924.5 | 2046.0 |
| y | 117,9 | 122,5 | 125,5 | 129,2 | 134,3 | 138,4 | 141,0 |
Здесь х – совокупные личные доходы;
y – текущие расходы на одежду среднестатистической американской семьи с 1996 по 2002 г.
Оценим регрессию y=ax+b.
 |
Ответ:
y=78,967+0.031x
Найдем коэффициент корреляции по формуле (2.2):
rxy=0.986
Построим график:
Вывод: С каждого дополнительного доллара американская семья в период 1996-2002 г. тратила 3,1 центов на текущие расходы на одежду.
Б)
| x | 1351.7 | 1369.3 | 1479.1 | 1682.5 | 1799.0 | 1924.5 | 2046.0 |
| y | 164,3 | 173,7 | 181,3 | 243,2 | 337,9 | 376,4 | 356,6 |
Здесь х – совокупные личные доходы;
y – текущие расходы на бензин, среднестатистической американской семьи с 1996 по 2002 г.
Оценим регрессию y=ax+b.
 |
Ответ:
y=-281,825+0.327x
Найдем коэффициент корреляциипо формуле (2.2):
rxy=0.962
Построим график:
Вывод: С каждого дополнительного доллара американская семья в период 1996-2002 г. тратила 32,7 центов на текущие расходы на бензин.
2. Вычислить коэффициенты регрессии общей суммы налогового сбора (переменная y) на сумму поступлений налога на добавленную стоимость (х) данным:
| Время наблюдения | y, млрд. руб. | x, млрд. руб. | xi2 | yi2 | xiyi |
| январь | 38,9 | 13,4 | 179,56 | 1513,21 | 521,26 |
| февраль | 45,3 | 15,4 | 237,16 | 2052,09 | 697,62 |
| март | 61,1 | 16,7 | 278,89 | 3733,21 | 1020,37 |
| апрель | 70,4 | 16,2 | 262,44 | 4956,16 | 1140,48 |
| май | 63,8 | 13,0 | 4070,44 | 829,4 | |
| июнь | 67,7 | 15,0 | 4583,29 | 1015,5 | |
| июль | 70,6 | 20,8 | 432,64 | 4984,36 | 1468,48 |
| август | 78,9 | 16,4 | 268,96 | 6225,21 | 1293,96 |
| сентябрь | 73,2 | 17,4 | 302,76 | 5358,24 | 1273,68 |
| октябрь | 78,1 | 23,6 | 556,96 | 6099,61 | 1843,16 |
| ноябрь | 103,0 | 23,9 | 571,21 | 2461,7 | |
| декабрь | 133,4 | 34,4 | 1183,36 | 17795,56 | 4588,96 |
| Σ | 884,4 | 226,1 | 4667,94 | 71980,4 | 18154,6 |
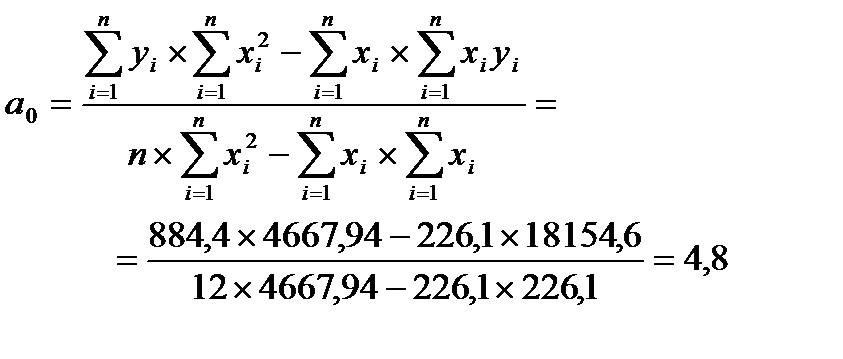
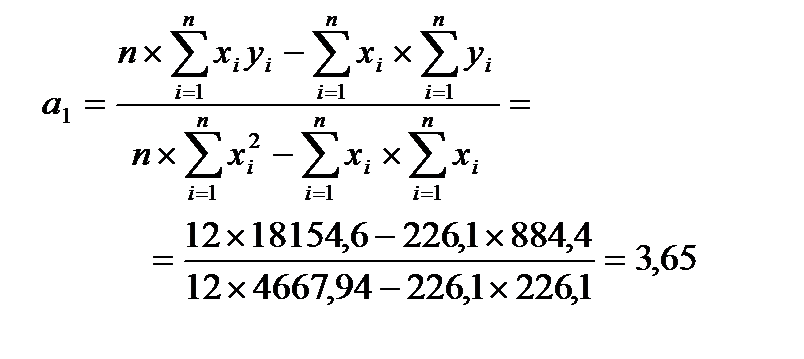
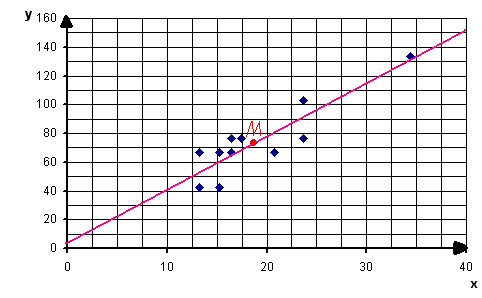 График уравнения регрессии y на x выглядит следующим образом:
График уравнения регрессии y на x выглядит следующим образом:
3. у= b +ахb и а - ?
| № | Х | Y | X2 | XY |
| -3 | -0,71 | 2,13 | ||
| -2 | -0,1 | 0,02 | ||
| -1 | 0,51 | -0,51 | ||
| 0,82 | ||||
| 0,88 | 0,88 | |||
| 0,81 | 1,62 | |||
| 0,49 | 1,47 | |||
| Сум å | 2,79 | 5,61 |
Оценим регрессию y=ax+b.
 |
Ответ:
y= 0,40+0,20x– уравнение линейной регрессии
4.х– мощность пласта, у– смена добычи угля.
| № | Х | Y | X2 | XY |
| Сум å |
a = 10*664-94*68 = 1.02
10*908-(94)2
b = 68-(-2,75)*94 = –2.75
Уравнение регрессии
y= 1,02x–2,75.
Коэфф. корреляции
R= n*åxy–åxåy=10*664 –94*68 =0.866
Ö(n*åx2– (x)2)(n*åy2– (åy)2)Ö(10*908– (94)2)(10*496– (68)2)
Связь между Х и Y ближе к линейной.
Коэфф. детерминации R2½R½£1
Þ 0.8662 = 0.749 Þ на 74,9% смена добычи угля зависит от мощности пласта и 25,1% от других факторов.
Контрольные вопросы
1. Что понимается под парной регрессией?
2. Какие задачи решаются при построении уравнения регрессии?
3. Какой вид имеет система нормальных уравнений метода наименьших квадратов в случае линейной регрессии?
4. По какой формуле вычисляется линейный коэффициент парной корреляции?
5. Как строится доверительный интервал для линейного коэффициента парной корреляции?
6. Как вычисляется индекс корреляции?
7. Как вычисляется и что показывает индекс детерминации?
8. Как проверяется значимость уравнения регрессии и отдельных коэффициентов?
9. Как строится доверительный интервал прогноза в случае линейной регрессии?
10. В чем сущность метода наименьших квадратов (МНК)?
11. Сформулируйте общую задачу статистической оценки параметров на примере оценки параметров линейной регрессии.
12. Сформулируйте свойства несмещенности, состоятельности и эффективности оценок параметров. Обладают ли этими свойствами оценки параметров линейной регрессии, полученные с помощью МНК?
13. В чем различие, смысловое и количественное, теоретических значений коэффициентов регрессии и их выборочных значений?
14. Какие факторы влияют на величину стандартных ошибок выборочных коэффициентов регрессии?
15. Как связаны выборочные коэффициенты регрессии с коэффициентом корреляции величин х и у?
16. Как осуществляется прогнозирование экономических показателей с использованием моделей линейной регрессии?
17. Как можно оценить «естественный» уровень безработицы с использованием модели линейной регрессии?
18. В каких случаях необходимо уточнение линейной регрессионной модели и как оно осуществляется?
Задания и задачи
1. Имеются следующие ряды оценок по тестам чтения и арифметики:
Чтение 43 58 45 53 37 58 55 61 46 64 46 62 60 56
Арифметика 32 25 28 30 22 25 22 20 20 30 21 28 34 28
Вычислите коэффициент корреляции.
2. Известны данные по числу преступлений на 100 тысяч человек, тыс. (y) в зависимости от среднедушевого дохода, тыс.руб. (x) по 10 регионам России. Построить линейную модель.
| y | 4,62 | 2,87 | 3,55 | 2,34 | 2,30 | 1,92 | 1,85 | 1,30 | 2,39 | 1,38 |
| x | 4,9 | 6,5 | 6,9 | 7,2 | 7,6 | 8,8 | 9,5 | 11,2 | 15,6 | 17,4 |
3. Дана зависимость зарплаты y, руб./мес. от стажа x, лет на некотором предприятии. Построить линейную модель.
| зарплата | стаж |
| 4 949 | |
| 9 094 | |
| 9 167 | |
| 11 836 | |
| 9 683 | |
| 9 927 | |
| 11 970 | |
| 10 607 | |
| 5 747 | |
| 15 327 | |
| 9 844 | |
| 4 953 | |
| 6 152 | |
| 9 109 | |
| 1 6235 | |
| 2 621 | |
| 13 702 | |
| 5 771 | |
| 15 416 | |
| 12 035 |
4. Известна доля владельцев персональных компьютеров 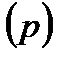 в зависимости от среднедушевого дохода
в зависимости от среднедушевого дохода 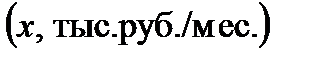 ; объем выборки
; объем выборки 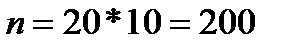 .
.
Логистическая модель:
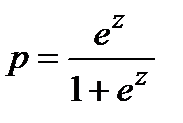 Þ
Þ 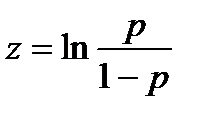
Построить линейную зависимость z от х.
| x | p | 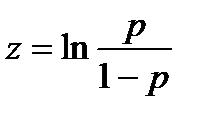 |
| 0,2 | -1,386 | |
| 0,1 | -2,197 | |
| 0,2 | -1,386 | |
| 0,3 | -0,847 | |
| 0,2 | -1,386 | |
| 0,6 | 0,405 | |
| 0,4 | -0,405 | |
| 0,8 | 1,386 | |
| 0,5 | ||
| 0,6 | 0,405 | |
| 0,6 | 0,405 | |
| 0,8 | 1,386 | |
| 0,7 | 0,847 | |
| 0,8 | 1,386 | |
| 0,8 | 1,386 | |
| 0,9 | 2,197 | |
| 0,7 | 0,847 | |
| 0,8 | 1,386 | |
| 0,9 | 2,197 | |
| 0,9 | 2,197 |
Тесты
1. Коэффициент корреляции, равный нулю, означает, что между переменными:
а) линейная связь отсутствует;
б) существует линейная связь;
в) ситуация не определена.
2. Коэффициент корреляции, равный –1, означает, что между переменными:
а) линейная связь отсутствует;
б) существует линейная связь;
в) функциональная зависимость;
г) ситуация не определенна.
3. Коэффициент регрессии показывает:
а) на сколько единиц своего измерения увеличится или уменьшится в среднем y, если x увеличить на единицу своего измерения;
б) долю дисперсии одной случайной величины, обусловленную вариацией другой;
в) на сколько % увеличится или уменьшится в среднем y, если x увеличится на 1 %.
4. Коэффициент регрессии изменяется в пределах от:
а) –1 до 1;
б) 0 до 1;
в) принимает любое значение.
5. В двумерной модели для вывода о независимости признаков х и y в генеральной совокупности достаточно проверить значимость:
а) только коэффициента корреляции;
б) коэффициента корреляции и регрессии;
в) коэффициента корреляции, детерминации и регрессии.
6. Если коэффициент корреляции положителен, то в линейной модели
a) с ростом х уменьшается у,
б) с ростом х увеличивается у,
в) с уменьшением х растёт у.
7.Если коэффициент корреляции отрицателен, то в линейной модели
a) с ростом х уменьшается у,
б) с ростом х увеличивается у,
в) с уменьшением х уменьшается у.
8.В модели парной регрессии у = 4 + 2х изменение х на 2 единицы вызывает изменение уна __ единиц
а) 2,
б) 4,
в) 6.
9. В парном регрессионном анализе коэффициент детерминации R2 равен
а) 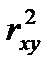 ,
,
б) 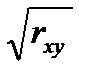 ,
,
в) 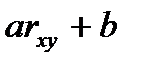 .
.
2.8. Самостоятельная работа студентов
Литература для самостоятельной работы
1. Эконометрика: Учебник./ Под ред. И.И. Елисеевой. – 2-е изд.– М.: Финансы и статистика, 2005. – 276 с.
2. Практикум по эконометрике. Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2005.
3. Мхитарян В.С., Архипова М.Ю., Сиротин В.П. Эконометрика: Учебно-методический комплекс. – М.: Изд. центр ЕАОИ. 2008. – 144 с.
4. ДоугертиКр. Введение в эконометрику/ Пер. с англ. – М.: МГУ; ИНФРА-М, 2003.
INTERNET-ресурсы
1. http://upereslavl.botik.ru/UP/ECON/econometrics/top1/tsld006.htm
2. http://www.nsu.ru/ef/tsy/ecmr/study.htm
3. http://www.nsu.ru/ef/tsy/ecmr/index.htm
4. http://www.statsoft.ru/home/textbook/def ault.htm
5. http://www.nsu.ru/ef/tsy/ecmr/study.htm
6. http://www.dataforce.net/~antl/article/econometric
7. http://www.nsu.ru/ef/tsy/ecmr/study.htm
8. http://www.tvp.ru/vnizd/mathem4.htm
9. http://www.kgtu.runnet.ru/WD/TUTOR/textbook/modules/stmulreg.html
