Основные элементы вероятностных расчетов
Введение
Здесь изложено содержание самостоятельной работы аспирантов в течение первого семестра обучения при изучении дисциплины «Теоретические основы статистической радиотехники». Данная дисциплина входит в вариативную часть учебного плана, направлена на подготовку к сдаче кандидатского экзамена и является теоретической базой при изучении остальных дисциплин учебного плана аспирантуры по направлению подготовки 11.06.01 «Электроника, радиотехника и системы связи» по профилям:
- «Радиотехника, в том числе системы и устройства телевидения»
- «Системы, сети и устройства телекоммуникаций»
Цель данной дисциплины – обеспечить освоение аспирантами базовых компетенций по практическому использованию теоретико-вероятностных методов при проведении научных исследований в рамках подготовки выпускной квалификационной работы и написании диссертационной работы.
Основная задача приводимых ниже заданий для самостоятельной работы – приобретение аспирантами навыков применения вероятностных моделей устройств, систем и сетей и процессов в них при анализе эффективности функционирования реального оборудования, оптимизации значений их параметров или при построении новых устройств.
Приводимые здесь задания являются минимально необходимым объемом самостоятельной работы в течение первого семестра обучения и основой при сдаче зачета по данной дисциплине как формы текущего контроля работы аспиранта.
Практикум содержит 3 части.
В первой части (раздел 1.2) содержатся индивидуальные задания, обеспечивающие возможность практического использования вероятностной терминологии в предметной области научных интересов аспиранта, приобретения навыков вероятностных вычислений в некоторых экспериментах со случайными исходами, построении графиков распределений вероятностей, функций распределения и плотностей вероятностей случайных величин, которые наиболее часто применяются в качестве математических моделей многих реальных величин в радиотехнике и телекоммуникациях.
Во второй части (раздел 1.3) аспирантам предлагается выполнить индивидуальные работы по освоению методов формирования выборок случайных величин и последующего их статистического анализа: генерирование случайных величин с заданной формой функции распределения, построение гистограмм и эмпирических функций распределения и их аппроксимация с помощью подходящих аналитических выражений. В методическом плане цель этой части – приобретение навыков выбора подходящих вероятностных моделей для реальных физических величин, типичных для предметных областей будущих научных исследований аспирантов.
В третьей части (раздел 1.4) аспиранты должны выполнить самостоятельно работу, которую можно рассматривать как обобщение заданий второй части – генерирование выборок случайных векторов и последующий их статистический анализ. Новыми элементами работы студентов здесь являются корреляционные матрицы, функции регрессии, многомерные эмпирические функции распределения и гистограммы, условные распределения.
Следует отметить, что практически все задания, связанные с вероятностными расчетами, статистическим анализом выборок и построением графиков, представляющих результаты работы аспирантов, составлены таким образом, что могут быть практически выполнены лишь при использовании современных программных комплексов. В качестве такового для аспирантов рекомендована лицензионная версия системы для научных исследований MATLAB&SIMULINK. Приобретение или совершенствование навыков решения вероятностных задач с применением таких комплексов является самостоятельной задачей данной дисциплины.
Основные элементы вероятностных расчетов
1.
1.1.
1.2.
Алгебра событий
Задача 1. Привести пример эксперимента со случайными исходами из области Ваших предметных исследований:
Ø описать комплекс условий  , при которых проводятся повторные испытания;
, при которых проводятся повторные испытания;
Ø определить термины: наблюдение, исход, совокупность всех исходов, совокупность исходов A, совокупность исходов B;
Ø определить термины: испытание, элементарное событие, пространство элементарных событий, событие А, событие В.
Задача 2. Доказать тождества для случайных событий:
- коммутативность 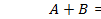 ;
;
- ассоциативность 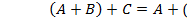 ;
;
- дистрибутивность 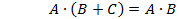 ;
;
- теоремы Де Моргана
a) 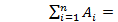 ,
,
б) 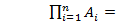 .
.
Планирование статистического эксперимента
Задача 7. Какой объем выборки необходимо выбрать, чтобы относительная среднеквадратическая ошибка оценки функции распределения этой случайной величины эмпирической функцией распределения не превысила 5%.
Рекомендации:
Вычисления выполнить для значения функции распределения при аргументе, равном медиане.
Рис.1. Гистограмма выборки случайной величины с гауссовским распределением
5) подсчитывается число элементов выборки  , относительная частота
, относительная частота  события
события 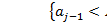
 и вычисляется значение гистограммы
и вычисляется значение гистограммы  на данномподинтервале;
на данномподинтервале;
6) на каждом подинтервале длины h строится прямоугольник с высотой  .
.
На рис. 1 изображена гистограмма, представляющая собой набор 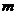 прямоугольников, ширина каждого из которых равна
прямоугольников, ширина каждого из которых равна 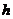 , а высота -
, а высота -  .
.
В MATLABимеется специальная функция hist, обеспечивающая возможность автоматизации процедуры построения гистограммы.
Вопросы для самопроверки
1. Поясните смысл термина «схема испытаний Бернулли».
2. Что такое «повторная выборка», «выборочное значение случайной величины»?
3. Что такое эмпирическая функция распределения? Для чего она нужна?
4. Дайте определение выборочного среднего и выборочной дисперсии. Какие свойства случайной величины характеризуют эти понятия?
5. Приведите пример события, связанного со случайной величиной. Что такое относительная частота события? Как она определяется?
6. Дайте определение начального момента второго порядка. Как он вычисляется?
7. Каким образом по гистограмме, построенной по выборочным значениям случайной величины в схеме испытаний Бернулли, можно получить представление о плотности вероятности этой случайной величины.
8. Приведите пример реальной физической величины, которую необходимо рассматривать как случайную величину.
Приложение 1.Датчики псевдослучайных чисел
1. Общая информация о датчиках
Равномерно распределенные псевдослучайные числа обычно генерируются детерминированным рекуррентным алгоритмом со значениями из интервала  . В качестве значения очередного элемента
. В качестве значения очередного элемента  выборки используется дробная часть значения некоторого специально выбранного сложного арифметического выражения, являющегося функцией от значения предшествующего элемента выборки
выборки используется дробная часть значения некоторого специально выбранного сложного арифметического выражения, являющегося функцией от значения предшествующего элемента выборки 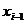 .
.
Обычно перед использованием датчика случайных чисел задается начальное значение 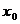 . Задание различных
. Задание различных 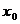 позволяет получать различные последовательности или различные выборки. В результате таких вычислений получают “квазислучайные” (псевдослучайные) числа. При увеличении объема выборки числа могут повторяться. Количество неповторяющихся чисел в выборке является параметром датчика, называемым периодом; значение периода является важным параметром датчика и может принимать значения от нескольких сотен тысяч до нескольких миллионов.
позволяет получать различные последовательности или различные выборки. В результате таких вычислений получают “квазислучайные” (псевдослучайные) числа. При увеличении объема выборки числа могут повторяться. Количество неповторяющихся чисел в выборке является параметром датчика, называемым периодом; значение периода является важным параметром датчика и может принимать значения от нескольких сотен тысяч до нескольких миллионов.
Квазислучайные числа с различными функциями распределения, отличными от равномерного, получают обычно из равномерно распределенных квазислучайных чиселс помощью соответствующих функциональных преобразований.
2 . Описание встроенных датчиков псевдослучайных чисел системы MATLAB
Используемая в лабораторном практикуме система MATLAB имеет встроенные датчики псевдослучайных чисел, которые можно использовать при имитационном моделировании радиотехнических систем и устройств в качестве источников случайных сигналов. При каждом обращении к такому датчику можно получить одно или заданное число выборочных значений случайной величины, обладающей известными вероятностными характеристиками. Обычно датчики позволяют получать выборки достаточно большого объема с независимыми элементами и известной функцией распределения. В данном разделе приводятся необходимые сведения о датчиках квазислучайных чисел, которые должны быть использованы при выполнении данной лабораторной работы.
2.1 . Формирование вещественного массива выборочных значений случайной величины, имеющей равномерное распределение на открытом интервале (0.0, 1.0)
Синтаксис:
y=rand(n,1)
Описание:
Функция MATLABy=rand(n,1) формирует матрицу размера  , элементами которой являются выборочные значения случайной величины, имеющей равномерное распределение на интервале (0,1). На рис.2 изображен график плотности вероятности
, элементами которой являются выборочные значения случайной величины, имеющей равномерное распределение на интервале (0,1). На рис.2 изображен график плотности вероятности  случайной величины с равномерным распределением, построенный с помощью функции MATLABw=unifpdf(x, 0,1), где w – массив значений функции
случайной величины с равномерным распределением, построенный с помощью функции MATLABw=unifpdf(x, 0,1), где w – массив значений функции  , x– массив значений аргумента этой функции.
, x– массив значений аргумента этой функции.
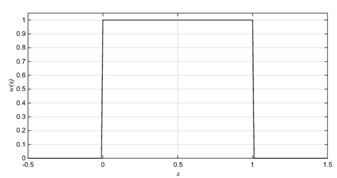
Рис. 2. Плотность вероятности случайной величины
Рис.5. Плотность вероятности случайной величины,
Рис.6. Плотность вероятности распределения Релея
График этой плотности, представлен на рис.6 для  .
.
График построен с помощью функции MATLAB 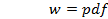 , где
, где  – массив значений аргумента плотности вероятности, для которого вычисляются значения
– массив значений аргумента плотности вероятности, для которого вычисляются значения  плотности
плотности  .
.
Пример:
pd = makedist(‘Rayleigh’, ‘  ’, 2);
’, 2);
y=random(pd, 10000, 1); % Выборкаобъемаn=10000;
x=0:0.01:15;
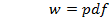 ;
;
plot(x,w)
2.6 . Формирование вещественного массива выборочных значений случайной величины, имеющей логарифмически нормальное распределение
Синтаксис:
pd = makedist(‘Lognormal’, ‘mu’, 2, ‘  , 1); w=
, 1); w=
y=random(pd, n, 1);
Функция y=random(pd, n,1) формирует выборку y размера  , элементами которой являются выборочные значениями случайной величины, имеющей логарифмически нормальное (логнормальное) распределение.
, элементами которой являются выборочные значениями случайной величины, имеющей логарифмически нормальное (логнормальное) распределение.
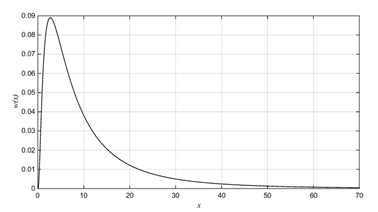
Рис. 7. Плотность вероятности логарифмически нормального распределения
Функция MATLABpd = makedist(‘Lognormal’, ‘mu’, 2, ‘  ’, 1) создает скрипт-файл логарифмически нормального распределения с параметром нецентральностиmu
’, 1) создает скрипт-файл логарифмически нормального распределения с параметром нецентральностиmu  и масштаба
и масштаба  .
.
Аналитическое выражение для соответствующей плотности вероятности имеет вид:
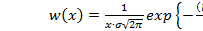 ,
,  .
.
График этой плотности для mu  и
и  приведен на рис.7.График построен с помощью функции MATLABw
приведен на рис.7.График построен с помощью функции MATLABw 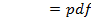 , где
, где  – массив значений аргумента плотности вероятности, для которого вычисляются значения wплотности
– массив значений аргумента плотности вероятности, для которого вычисляются значения wплотности  .
.
Пример:
pd = makedist(‘Lognormal’,’mu’,2, ‘  ’, 2);
’, 2);
y=random(pd, 10000, 1); % Выборкаобъема n=10000;
x=0:0.01:70;
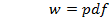 ;
;
plot(x,w)
2.7 . Формирование вещественного массива выборочных значений случайной величины, имеющей полигауссовское распределение
Синтаксис:
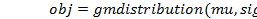 ;
;
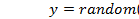 ;
;
Описание:
mu– матрица размера  , определяющая математические ожидания
, определяющая математические ожидания  гауссовских случайных величин, являющихся компонентами смеси;
гауссовских случайных величин, являющихся компонентами смеси;
 – определяет ковариации каждой компонентысмеси; размер матрицы
– определяет ковариации каждой компонентысмеси; размер матрицы  в данной работеравен
в данной работеравен  ;
;
 – вектор размера
– вектор размера  , определяющий вероятности появления выборочных значений гауссовских компонент.
, определяющий вероятности появления выборочных значений гауссовских компонент.
Функция 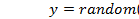 формирует матрицуразмера
формирует матрицуразмера  выборочных значений случайной величины с плотностьювероятности obj.
выборочных значений случайной величины с плотностьювероятности obj.
Полигауссовская плотность вероятности может быть задана аналитически следующим выражением :
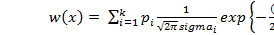 ,
, 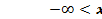 .
.
На рис.8 представлен график полигауссовской плотности для следующих численных значений параметров:
 .
.
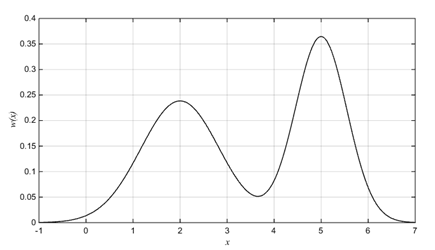
Рис.8. Плотность полигауссовского распределения
График построен с помощью функции MATLAB  . Здесь
. Здесь  – массив значений плотности вероятности objдля значений [-1:0.01:7]аргумента
– массив значений плотности вероятности objдля значений [-1:0.01:7]аргумента  .
.
Пример:
obj= gmdistribution([2 5]’,  ;
;
y=random(obj, 10000); % Выборкаобъемаn=10000;
x=0:0.01:7;
 ;
;
plot(x,w)
3.8 . Приложение 2. Выбор вариантов
Таблица 1
| № вар. | Распределение | Значения параметров плотности вероятности |
| 1. | Хи-квадрат | 1.1:  1.2: 1.2:  1.3: 1.3:  1.4: 1.4:  |
| 2. | Релея | 2.5:  2.6: 2.6:  2.7: 2.7:  2.8: 2.8:  |
| 3. | Райса | 3.9: s  ; 3.10: ; 3.10: 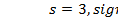 ; 3.11: ; 3.11: 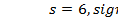 ; 3.12: ; 3.12: 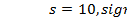 ; ; |
| 4. | Логнормальное | 4.13: 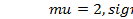 ; 4.14: ; 4.14: 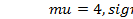 ; 4.15: ; 4.15: 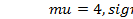 ; 4.16: ; 4.16:  ; ; |
| Полигауссовское | 5.17:  5.18: 5.18: 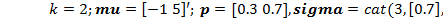 5.19: 5.19:  5.20: 5.20: 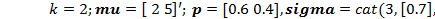 5.21: 5.21: 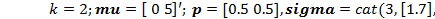 | |
Номер варианта работы, выполняемого студентом, определяется номером его фамилии в журнале группы, который определяет второе число во втором столбце табл. 1.
3.9. Приложение 3. Пример исследования 1
В данном разделе приведен пример исследования случайной выборки, полученной с помощью датчика случайных чисел с нормальным распределением с нулевым математическим ожиданием (  ) и дисперсией, равной 1 (
) и дисперсией, равной 1 (  ).
).
В соответствии с изложенным в Приложении 1 в системе MATLAB генератор квазислучайных чисел с таким распределением и значениями параметров его плотности вероятности оформлен как m-функция. Обращение к такому генератору в строке командного окна MATLAB должно быть записано следующим образом:
y=randn(n, 1);
n – размер формируемой выборки. В результате выполнения этой команды в массив y (вектор-столбец) рабочего пространства будет помещена выборка, сформированная этим датчиком.
Ниже приведены все команды системы MATLAB, необходимые для вычисления и построения гистограммы выборки и графика теоретической плотности вероятности гауссовской случайной величины.
% Построение и аппроксимация гистограммы выборки %
randn('seed',0) ; % Устанавливает датчик псевдослучайных чисел в исходное состояние; %
normal=randn(10000,1); % Датчик randn формирует матрицу размера 10000х1, элементами которой являются выборочные значения случайной величины, имеющей нормальное распределение с математическим ожиданием 0 и дисперсией 1; матрица помещена в массив с именем normalрабочего пространства%
m=mean(normal); % Вычисление значения начального выборочного момента первого порядка - среднеарифметического значения выборки (оценка математического ожидания случайной величины;%
sigma=std(normal); % Вычисление значения второго центрального выборочного момента - среднеквадратического отклонения случайной величины от математического ожидания;%
[N,X]=hist(normal,25); % Выборка normalобрабатывается функцией MATLABhist(вычисление ненормированной гистограммы), для которой выбрано число подинтервалов  . Здесь N - вектор, i-тая компонента которого равна числу элементов выборки, попавших в i-тыйподинтервал; Х - вектор, i-тая компонента которого определяет положение на оси абсцисс центра i-го подинтервала; %
. Здесь N - вектор, i-тая компонента которого равна числу элементов выборки, попавших в i-тыйподинтервал; Х - вектор, i-тая компонента которого определяет положение на оси абсцисс центра i-го подинтервала; %
bar(X, N/(10000*(X(2)-X(1))),’g-‘)% Вычисление значений и построение гистограммы выборки; %
hold; % Данная команда устанавливает режим сохранения текущего графического окна, что позволяет в этом окне построить последовательно несколько графиков;%
plot(X, exp(-(X-m).^2/(2*sigma^2))/((sqrt(2*pi)*sigma)),'r-')%Вычисление значений и построение графика функции плотности вероятности %;
title(‘Гистограмма выборки из гауссовского распределения’); % Заголовок рисунка %
xlabel(‘Значения случайной величины’);
ylabel(‘Значения плотности вероятности');
grid; % Нанесение координатной сетки; %

Рис. 8. Гистограмма выборки стандартной гауссовской случайной величины
На рис. 8 представлены графики, полученные в результате выполнения приведенных выше команд системы MATLAB.
3.10. Приложение 4. Пример исследования 2
В данном разделе приведен пример статистической обработки случайной выборки, полученной с помощью датчика случайных чисел с нормальным распределением с математическим ожиданием  и среднеквадратическим отклонением sigma.
и среднеквадратическим отклонением sigma.
В системе MATLAB генератор квазислучайных чисел с таким распределением и заданными значениями параметров его плотности вероятности оформлен как m-функция. Обращение к такому генератору в строке командного окна MATLAB должно быть записано следующим образом:
y=normrnd(a, sigma, n, 1);
гдеn – размер формируемой выборки. В результате выполнения этой команды в массив y (вектор-столбец) рабочего пространства системы MATLAB будет помещена выборка, сформированная этим датчиком.
Ниже приведены все команды системы MATLAB, необходимые для вычисления и построения эмпирической функции распределения и графика теоретической функции распределения рассматриваемой здесь гауссовской случайной величины.
%Построение и аппроксимация эмпирической функции распределения%
norma=normrnd(10, 1, 50,1); % Датчик normrnd формирует матрицу размера 50х1, элементами которой являются выборочные значения случайной величины, имеющей нормальное распределение с математическим ожиданием 10 и среднеквадратическим отклонением 1; матрица помещена в массив с именем normaрабочего пространства MATLAB %
cdfplot(norma) %Вычисление и построение графика эмпирической функции распределения  по выборкеnorma%
по выборкеnorma%
hold on
x=2:0.1:20;
F=normcdf(x, 10, 1);
plot(x,F,’r-‘)
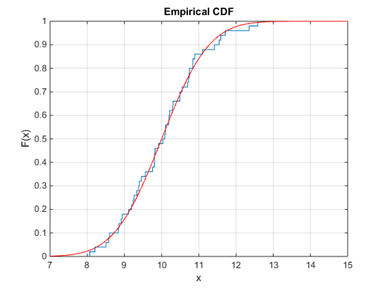
Рис. 9. Построение и аппроксимация эмпирической функции распределения
Приложение5. Некоторые функции MATAB, полезные при исследовании распределений случайных величин
1. Вычисление значений функции распределения при известной плотности вероятности:
pd=makedist(‘Normal’);
x=-3:.1:3;
cdf_normal=cdf(pd, x);
2. Вычисление и построение гистограммы выборки с последующей аппроксимацией теоретической кривой:
y=normrnd(10,2,1000,1);
figure(2)
histfit(y)
3. Вычисление и построение гистограммы выборки с заданным числом столбцов и сглаживание ее заданной плотностью вероятности:
b=betarnd(3,10,1000,1);
figure(3)
histfit(b,15,’beta’)
4. Графический интерфейс для исследования влияния изменения значений параметров на форму плотности вероятности и функции распределения:
disttool
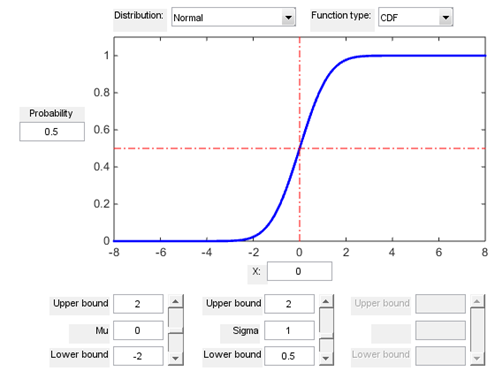
Рис.10.
Можно выбрать вид распределения, тип функции и установить различные значения параметров этого распределения, после ввода которых автоматически строится график плотности или функции распределения.
Для случайного вектора
Цель работы
Экспериментальное исследование функций распределения и плотностей вероятностей случайных векторов методом статистического моделирования на ЭВМ с использованием системы научных и инженерных расчетов MATLAB. Основное содержание работы:
- моделирование в схеме испытаний Бернулли выборки заданного объема векторной случайной величины с известной плотностью вероятности;
- построение гистограммы;
- аппроксимация гистограммы теоретической кривой;
- построение эмпирической функции распределения и ее аппроксимация теоретической кривой;
- вычисление теоретических и статистических числовых характеристик (математических ожиданий и дисперсий компонент, коэффициентов корреляции).
Все студенты должны самостоятельно выполнить все пункты для гауссовского случайного векторапри заданных преподавателем численных значений параметровраспределений этого вектора.
4.2. Предварительная подготовка к выполнению работы
1. Изучить рекомендованные разделы, указанные в списке литературы.
2. Подготовить ответы на контрольные вопросы, приведенные в конце описания лабораторной работы.
3. По таблице № 1 определить номер выполняемого индивидуального варианта. Записать явные выражения для функции распределения и плотности вероятностисоответствующего случайного вектора, начальные и центральные моменты первого и второго порядка компонент вектора, их выборочные аналоги, ковариационной матрицы и выборочные аналоги элементов этой матрицы.
4. Изучить приложение 2 к данной работе, содержащее некоторые рекомендации по использованию системы MATLAB при её выполнении и соответствующие примеры, обратив особое внимание на правила задания функций, ввод численных значений параметров, построение графиков на экране дисплея.
5. Составить письменно разделы диалога с системой MATLAB в интерактивном режиме, каждый из которых обеспечивает выполнение одного из пунктов задания на экспериментальное исследование в лаборатории.
6. Подготовить бланк отчета принятой на кафедре формы о выполнении лабораторной работы с результатами предварительных расчетов.
Выполнение исследований
1. Убедиться в активности системы MATLAB по наличию на экране дисплея командного окна с приглашением к работе (Ready). Проверить список переменных в рабочем пространстве системы (who,whos); освободить рабочеe пространство, если необходимо (clear)[3].
2. Составить текст скрипт-файла, обеспечивающего выполнение всех пунктов задания на исследования в лаборатории. Запуская эту программу на выполнение внести все исправления, рекомендуемые системой MATLAB[4]. Окончательный текст скрипт-файла сохранить в папку группы с индивидуальным именем и номером лабораторной работы.
3. Используя созданный скрипт-файл и численные значения параметров личного варианта, построить поверхности теоретической плотности вероятности (figure (1)) и функции распределения (figure(2)) случайного вектора.
4. Для этих же значений параметров создать исходную выборку(двумерный массив) заданного объема значений исследуемого случайного вектора. Построить гистограмму на основе исходной выборки, получив ее изображение на экране монитора (figure(3)).
5. Используя исходную выборку вычислить выборочные значения начальных и центральных моментов случайного вектора: оценки математических ожиданий, дисперсий компонент случайного вектора и элементов его ковариационной матрицы. Полученные значения оценок внесите в соответствующий пункт отчета для сравнения с их истинными значениями.
6. В индивидуальной папке студента, находящейся в папке группы, сохраните отлаженный файл лабораторной работы для предъявления преподавателю при ее защите.
7. Сформулируйте в письменном отчете свои основные выводы и опишите полученные результаты проведенного исследования.
Содержание отчета
Отчет должен содержать следующие разделы:
1. Цель работы;
2. Вероятностные характеристики случайного вектора: аналитические выражения для совместной плотности вероятности, совместной функции распределения и начальных и центральных моментов случайного вектора;
3. Статистические характеристики случайного вектора: выражения для двумерной гистограммы, эмпирической функции распределения, эмпирических начальных и центральных моментов компонент вектора, элементов ковариационной матрицы;
4. Результаты экспериментальных исследований, полученные в лаборатории: истинные значения параметров случайного вектора и их оценки; графики представляются при защите работы в результате выполнения соответствующего файла.
5. Письменно сформулированные в отчете выводы на основе полученных результатов проведенного исследования.
Задание 7
Случайные величины  и
и  являются совместно гауссовскими с нулевыми математическими ожиданиями, дисперсиями
являются совместно гауссовскими с нулевыми математическими ожиданиями, дисперсиями 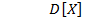 ,
, 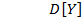 и коэффициентом корреляции
и коэффициентом корреляции  . Построить график условной плотности вероятности случайной величины
. Построить график условной плотности вероятности случайной величины  при условии, что случайная величина
при условии, что случайная величина  в проведенном испытании приняла значение
в проведенном испытании приняла значение  , а
, а  , где
, где  –номер Вашей фамилии в журнале группы.
–номер Вашей фамилии в журнале группы.
Рис.1. Гистограмма выборки случайной вектора с гауссовским распределением
На рис. 1 изображена 3-х мерная гистограмма, представляющая собой набор параллелепипедов с основаниями  и высотой -
и высотой -  .
.
Вопросы для самопроверки
1. Поясните смысл термина «схема испытаний Бернулли».
2. Что такое «повторная выборка», «выборочное значение случайной величины»?
3. Что такое эмпирическая функция распределения? Для чего она нужна?
4. Дайте определение выборочного среднего и выборочной дисперсии. Чтохарактеризуютэтипонятия?
5. Приведите пример события, связанного со случайным вектором. Что такое относительная частота события? Как она определяется?
6. Дайте определение начального смешанного момента второго порядка. Как он вычисляется?
7. Каким образом по гистограмме, построенной по выборочным значениям случайного вектора в схеме испытаний Бернулли, можно получить представление о совместной плотности вероятности компонент этого случайного вектора.
8. Приведите пример реальных физических величин, которые необходимо рассматривать как случайный вектор.
4.10. Приложение 1. Полезные функции MATLAB
1.1. Размещение наинтервала  заданного числа
заданного числа  точек:
точек:
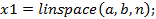
Пример:
>> x=linspace(0, 3, 3)
x =
0 1.5000 3.0000
1.2. Построение 2-х мерной решетки на плоскости:
Пример:
[X1, X2]=meshgrid(1:1:2, 4:2:8)
Переменная X1 принимает 2 значения: 1 и 2:
X1 =
1 2
1 2
Переменная X2 принимает 3 значения: 4, 6 и 8
X2 =
4 4
6 6
8 8
Все строки массива X содержат все возможные значения пар (X1, X2)на решетке
X=[X1(:) X2(:)]; % Двумерный массив
X’ =
1 1 1 2 2 2
4 6 8 4 6 8
1.3. Построение поверхности двумерной плотности вероятности
mu=[ 4 3]; % Вектор-строка математических ожиданий компонент.
sigma= [1 -0.4; -0.4 0.25]; % Ковариационная матрица.
[x1, x2] = meshgrid(linspace(0,8,40), linspace(0, 6, 30));
X=[x1(:) x2(:) ];
pd=mvnpdf(X, mu, sigma);
figure(2)
surf(x1, x2, reshape(pd, 30, 40)); % Построение поверхности
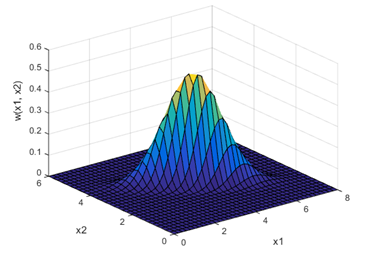
Рис. 2. Двумерная плотность вероятности гауссовского вектора
1.4. Построение поверхности двумерной функции распределения
pc=mvncdf(X, mu, sigma);% Используются данные п. 1.3
figure(3)
surf(x1, x2, reshape(pc, 30, 40));% Используются данные п. 1.3
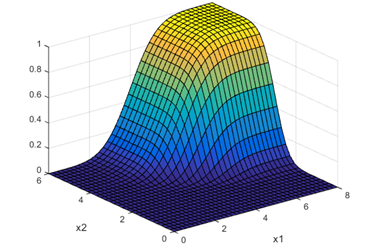
Рис.3. Совместная функция распределения компонент гауссовского вектора
1.5. Формирование выборки гауссовского вектора
R=mvnrnd(mu, sigma, n); % mu – вектор-строка математических ожиданий размера 1хd, sigma – ковариационная матрица размера  . n – объем выборки.
. n – объем выборки.
R –выборка значений d-мерного вектора – матрица размера  .
.
1.6. Построение двумерной гистограммы
figure(4)
hist3(R,[16 12]);% Используются данные п.1.3.
xlabel( ‘ x1’); ylabel( ‘ x2 ‘);
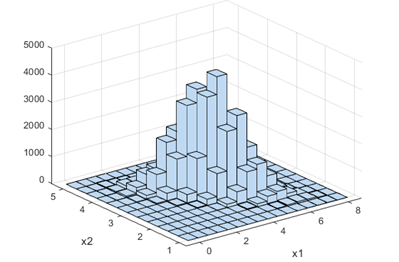
Рис. 4. Гистограмма двумерного гауссовского вектора
Дополнительные сведения о функциях MATLAB, полезных при работе со случайными величинами, можно найти в [3].
4.11. Приложение 2. Выбор вариантов
Таблица 1. Варианты значений параметров двумерной гауссовской плотности вероятностей
| № вар. | 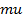 | 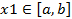 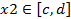 | 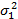 | 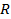 | 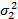 | |||
| a | b | c | d | |||||
| 1. | 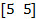 | 1.2 | ||||||
| 2. | 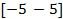 | -10 | -10 | 1.0 | 0.4 | 1.2 | ||
| 3. | 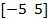 | -10 | 1.1 | 0.8 | 1.42 | |||
| 4. | 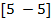 | -10 | 0.8 | 0.95 | 2.01 | |||
| 5. | 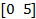 | -5 | 1.5 | 0.2 | ||||
| 6. | 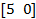 | -5 | 1.1 | -1 | 0.25 | |||
| 7. | 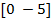 | -5 | -10 | 1.0 | -0.95 | 1.12 | ||
| 8. | 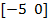 | -10 | -5 | 1.2 | -0.85 | |||
| 9. | 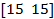 | 1.3 | -0.5 | 2.1 | ||||
| 10. | 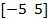 | -10 | -0 | 1.5 | 0.2 | |||
| 11. | 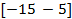 | -20 | -10 | -10 | 1.3 | 0.82 | ||
| 12. | 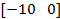 | -15 | -5 | -5 | 1.2 | 0.24 | 1.3 | |
| 13. | 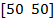 | 1.17 | -0.3 | 1.28 | ||||
| 14. | 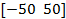 | -55 | -45 | -45 | 1.09 | |||
| 15. | 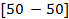 | -55 | -45 | 1.6 | 0.8 | 1.72 | ||
| 16. | 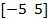 | -55 | -45 | -55 | -45 | 1.21 | 0.5 | 0.2 |
| 17. | 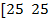 | 1.25 | 0.2 | 1.25 | ||||
| 18. | 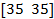 | 1.32 | -0.5 | 0.2 | ||||
| 19. | 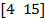 | -1 | 1.62 | -0.9 | 2.1 | |||
| 20. | 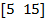 | 1.21 | -0.99 | 2.5 | ||||
| 21. | 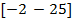 | -7 | -30 | -20 | 1.2 | |||
| 22. | 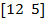 | 1.72 | 0.3 | 2.8 | ||||
| 23. | 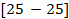 | -30 | -20 | 1. | 0.8 | 2.9 | ||
| 24. | 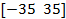 | -40 | -30 | 1.2 | -0.5 | 0.92 | ||
| 25. |
|
