Решить задачу математической статистики

а. Найти математическое ожидание случайной дискретной величины

б. Найти дисперсию случайной дискретной величины

в. Вычислить среднее квадратичное случайной дискретной величины

	хi pi 0,2 0,5 0,3		хi pi 0,3 0,3 0,2 0,2
	хi pi 0,2 0,3 0,5		хi pi 0,3 0,3 0,15
	хi pi 0,2 0,3		хi pi 0,3 0,2 0,1 0,4
	хi pi 0,3 0,5 0,2		хi pi 0,2 0,3 0,2 0,3
	хi pi 0,3 0,4 0,3		хi pi 0,15 0,25 0,4 0,2
хi pi 0,2 0,5 0,3		хi pi 0,3 0,3 0,2 0,2
хi pi 0,2 0,3 0,5		хi pi 0,3 0,3 0,15
хi pi 0,2 0,3

7. Образец варианта контрольной работы

1. Вычислить значение производной функции

а) у = б) у =

2. Найти максимум и минимум функции

3. Найти неопределенный интеграл

а) б)

4. Вычислить определенный интеграл

а)

5. Вычислить площадь криволинейной трапеции с помощью определенного интеграла

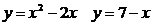
6. Заданы матрицы А, В и С, выполнить действия

7. Решить систему уравнений двумя способами

методом Крамера

методом обратной матрицы

8. Выполнить действия

9. .Решить задачу, используя классическое определение вероятности

Из урны, в которой находятся 5 белых и 7 черных шаров вынимают один шар. Какова вероятность, что шар окажется черным Решить задачу математической статистики

а Найти математическое ожидание случайной дискретной величины

б. Найти дисперсию случайной дискретной величины

в. Вычислить среднее квадратичное случайной дискретной величины

хi pi 0,2 0,5 0,3

10.

Вариант решения контрольной работы

1. Вычислить значение производной функции

а) у = б) у =

Решение

Ответ:

2. Найти максимум и минимум функции

Решение:

1. Находим производную функции

2. Находим критические точки функции, решив уравнение:

3.Определим промежутки возрастания и убывания функции:

Ответ:

3. Найти неопределенный интеграл

а) б)

Решение:

Ответ:

4. Вычислить определенный интеграл

Решение:

Ответ:

5. Вычислить площадь криволинейной трапеции с помощью определенного интеграла

Решение: Найдем пределы интегрирования, предварительно приравняв уравнения: получим

отсюда следует, что пределы интегрирования равны

Далее построим графики данных функций в одной и той же координатной системе:

Площадь полученной криволинейной трапеции, ограниченной линиями находим по формуле Ньютона- Лейбница: , где a и b- пределы интегрирования

в нашем случае a=-2,и b=3

Итак,

Ответ:

6. Заданы матрицы А, В и С, выполнить действия

Решение:

1. Выполним умножение матриц А и С:

2 Найдем сумму матриц

Ответ:

7. Решить систему уравнений двумя способами

методом Крамера

методом обратной матрицы

Решение:

1.Методом Крамера

Если определитель системы отличен от нуля (D ¹ 0), то система имеет единственное решение, которое находится по формулам: , где ∆₁, ∆₂, ∆₃ - дополнительные определители, которые получаются из определителя системы заменой одного из столбцов столбцом свободных членов:

Вычислим

Система имеет единственное решение.

Вычислим

Проверка

Система решена верно.

2. методом обратной матрицы

В матричном исчислении система имеет вид AxX=B, где A- матрица системы, Х- матрица неизвестных, В- матрица свободных членов, т.е. для решения найдем обратную матрицу и, умножив обе части уравнения AxX=B на слева найдем решение системы, т.е.

Для вычисления им А^-1сначала для этого найдем определитель системы:

Матрица А невырожденная и имеет обратную матрицу.

Найдем алгебраические дополнения:

; ; ; ; ; ; ; ; ;

Обратная матрица имеет вид

Проверим правильность нахождения Выполним умножение

Обратная матрица найдена верно.

Проверка:

Ответ:

8. Выполнить действия

Решение:

9. .Решить задачу, используя классическое определение вероятности

Из урны, в которой находятся 5 белых и 7 черных шаров вынимают один шар. Какова вероятность, что шар окажется черным?

Решение. Обозначим событие, состоящее в появлении черного шара, через А. Общее число случаев есть n = 5 + 7=12. Число случаев m, благоприятствующих появлению события А, равно По формуле Р (А) = получим

Ответ: Вероятность того, что вынутый шар окажется черным равна