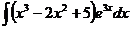Основные методы интегрирования.

Найти интеграл, используя подходящую подстановку:

6.2.1. 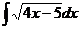6.2.2.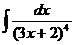

6.2.3. 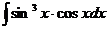6.2.4.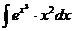

6.2.5. 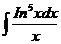6.2.6.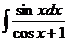

6.2.7. 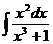6.2.8.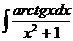

6.2.9. Найти интеграл с помощью подстановки, предварительно преобразовав подынтегральное выражение:

1) 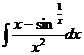2)

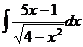
Решение: 1) Представим исходный интеграл в виде разности двух интегралов:

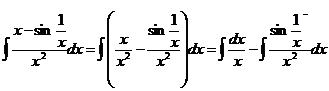
Первый из двух последних интегралов – табличный, а во втором надо сделать подстановку 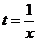. Тогда 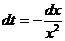, откуда 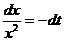. Следовательно,

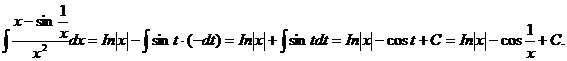
2) Запишем данные интегралы как разность двух интегралов:

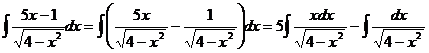
Второй из двух полученных интегралов – табличный, а в первом сделаем подстановку 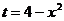, при этом условимся писать все вспомогательные выкладки и обозначения, относящиеся к данной подстановке, в квадратных скобках под соответствующим интегралом. В частности,

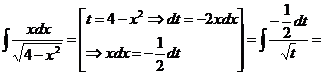
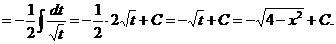
Таким образом,

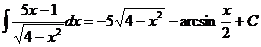
Найти интегралы с помощью подстановки, предварительно преобразовав подынтегральные выражения:

6.2.10. 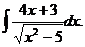6.2.11.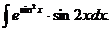

6.2.12. 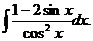6.2.13.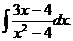

6.2.14. Найти интеграл, используя подходящую подстановку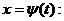

1)

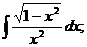
2)

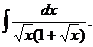
Решение: 1) Сделаем такую замену 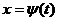, чтобы подкоренное выражение 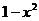стало полным квадратом. Подходит, например, подстановка 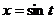(или 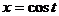). Тогда

=

=

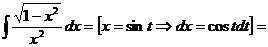
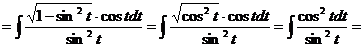
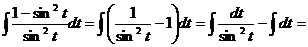
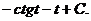
Учитывая, что 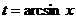, получим окончательно:

=

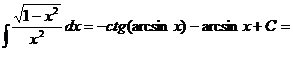
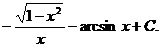
2) Сделаем замену 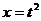, чтобы корни извлекались нацело:

=

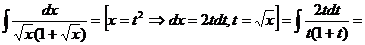
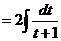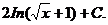
Найти интегралы, используя подходящую подстановку :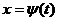

6.2.15. 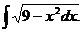6.2.16.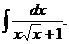

6.2.17. 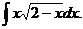6.2.18.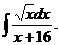

6.2.19. Найти интеграл

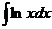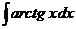1) . 2) . 3) .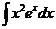

.

Решение: 1) Положим 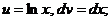тогда 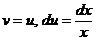. Используя формулу интегрирования по частям 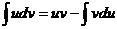, получаем .

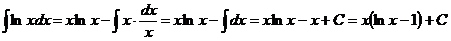2) Пусть 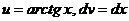, тогда 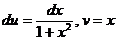. По формуле интегрирования по частям находим .

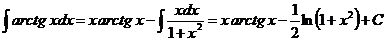3) Положим 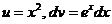; тогда 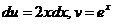. Применяем формулу интегрирования по частям: .

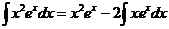Мы добились понижения степени х на единицу. Чтобы найти 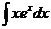, применим ещё раз интегрирование по частям. Полагаем 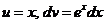; тогда 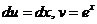и .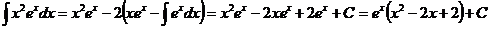

Найти интегралы, использую интегрирование по частям:

6.2.20. 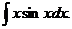6.2.21.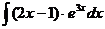

6.2.22. 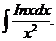6.2.23.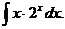

6.2.24. 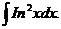6.2.25.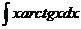

6.2.26. Найти интеграл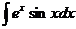

Решение: Пусть u=e^x, dv=sinxdx; тогда du=e^xdx, v=-cosx. Следовательно, =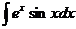

=-e^xcosx+ 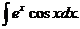Создается впечатление, что интегрирование по частям не привело к цели, так как интеграл не упростился. Попробуем еще раз проинтегрировать по частям. Приняв u=e^x, dv=cosxdx, откуда du=e^xdx, v=sinx, получаем 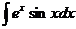= - e^xcosx+(е^хsinx- - 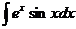), т.е. 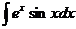= - е^хcosx+e^xsinx- .

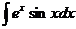Применив дважды операцию интегрирования по частям, мы в правой части снова получили исходный интеграл. Таким образом, приходим к уравнению с неизвестным интегралом 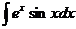. Из этого уравнения находим

2 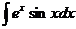= - е^хcosx+e^xsinx, т.е. 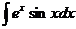= 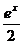(sinx-cosx)+C.

Найти интегралы:

6.2.27. 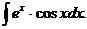6.2.28.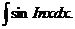

При вычислении некоторых интегралов приходится комбинировать подстановку с методом интегрирования по частям.

6.2.29. Найти интеграл .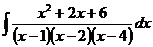

Решение: Так как каждый из двухчленов 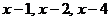входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы простейших дробей I типа:

.

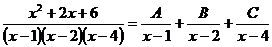Освобождаясь от знаменателей, получим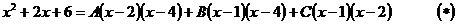

Следовательно,

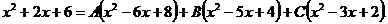
Сгруппируем члены с одинаковыми степенями:

.

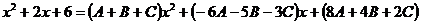Сравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений

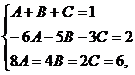
из которой найдём .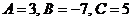

Итак, разложение рациональной дроби на простейшие имеет вид

.

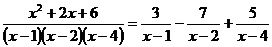Неизвестные А, В, С в разложении можно было определить и иначе. После освобождения от знаменателя можно придать х столько частных значений, сколько содержится в системе неизвестных, в данном случае – три частных значения.

Особенно удобно придавать х значения, являющиеся действительными корнями знаменателя. Применим этот приём к решению данного примера. После освобождения от знаменателя мы получили равенство 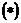. Действительными корнями знаменателя являются числа 1, 2 и 4. Положим, что в этом равенстве х=1, тогда 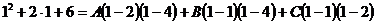, откуда 9=3А, т. е. А=3. Полагая х=2, получаем 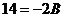, т. е. 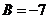; полагая 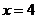, имеем 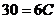, т. е. 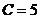. В результате получились те же значения, что и при первом способе определения неизвестных. Таким образом,

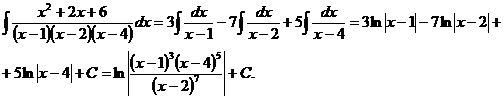
6.2.30. Найти интеграл .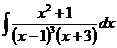

Решение: Множителю 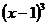соответствует сумма трёх простейших дробей 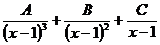, а множителю 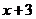простейшая дробь 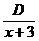. Итак,

.

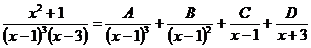Освободимся от знаменателя:

.

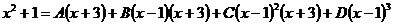Действительными корнями знаменателя являются числа 1 и –3. Полагая 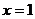, получаем 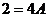, т. е. 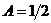. При 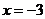имеем 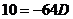, т. е. .

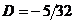Сравним теперь коэффициенты при старшей степени х, т. е. при 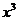. В левой части нет члена с 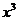, т. е. коэффициент при 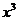равен 0. В правой части коэффициент при 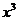равен C+D. Итак C+D=0, откуда .

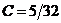Остаётся определить коэффициент В. Для этого необходимо иметь ещё одно уравнение. Это уравнение можно получить путём сравнения коэффициентов при одинаковых степенях х (например, при 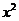) или придав х какое-нибудь числовое значение. Удобнее взять такое значение, при котором вычислений будет возможно меньше. Полагая, например, 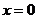, получаем

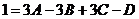, или 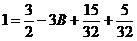, т. е. .

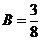Окончательное разложение данной дроби на простейшие имеет вид

.

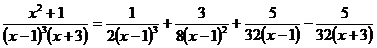Таким образом, получаем

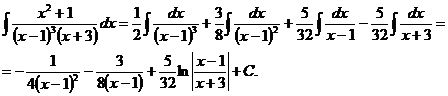
6.2.31. Найти интеграл .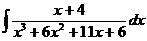

Решение: Так как подынтегральная функция является правильной дробью, то её следует сразу представить в виде суммы простейших дробей. Легко видеть, что многочлен 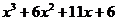обращается в нуль при 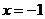, поэтому он делится без остатка на 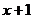. Выполним деление:

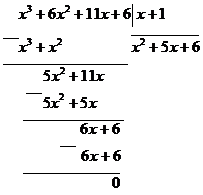
Следовательно,

;

.

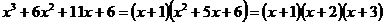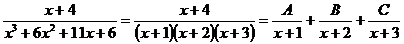Освобождаясь от знаменателей, получим

.

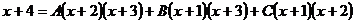Полагая 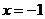, найдём 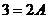, т. е. 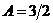. Если 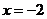, то получим 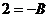, т. е. 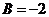. При 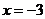получим 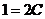, т. е. .

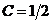Итак,

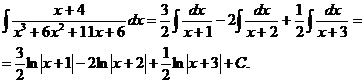
Разное.

Найти интегралы, используя подходящую подстановку:

6.2.32. 6.2.33.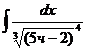

6.2.34. 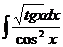6.2.35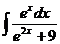

6.2.36. 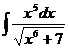6.2.37.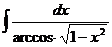

6.2.38. 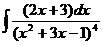6.2.39.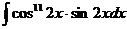

6.2.40. 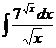6.2.41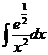

6.2.42. 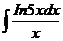6.2.43.

6.2.44 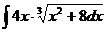6.2.45.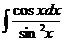

6.2.46. 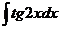6.2.47.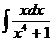

6.2.48. 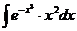6.2.49.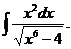

6.2.50. 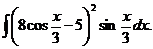6.2.51.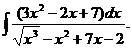

6.2.52. 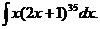6.2.53.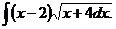

Найти интегралы, предварительно преобразовав подынтегральные выражения:

6.2.54. 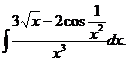6.2.55.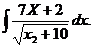

6.2.56. 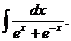6.2.57.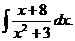

6.2.58. 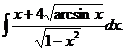6.2.59.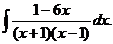

6.2.60.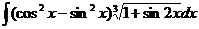

6.2.61.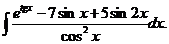

Найти интегралы, используя подходящую подстановку :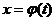

6.2.62. 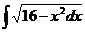. 6.2.63.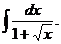

6.2.64. 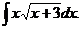6.2.65. .

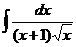6.2.66. 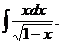6.2.67.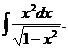

Найти интегралы, используя интегрирование по частям:

6.2.68. 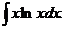6.2.69.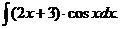

6.2.70. 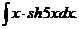6.2.71.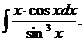

6.2.72. 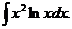6.2.73.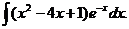

6.2.74 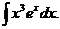6.2.75.

6.2.76. 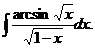6.2.77.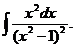

6.2.78. 6.2.79.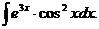

Разное.

Вычислить неопределенный интеграл

6.2.80. 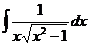6.2.81.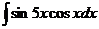

6.2.82. 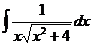6.2.83.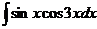

6.2.84. 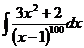6.2.85.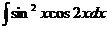

6.2.86. 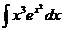6.2.87.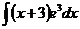

6.2.88. 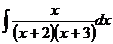6.2.89.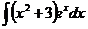

6.2.90. 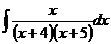6.2.91.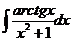

6.2.92. 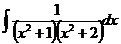6.2.93.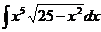

6.2.94. 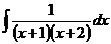6.2.95.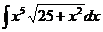

6.2.96. 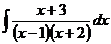6.2.97.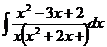

6.2.98. 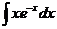6.2.99.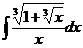

6.2.100. 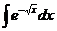6.2.101.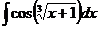

6.2.102. 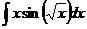6.2.103.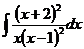

6.2.104. 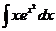6.2.105.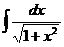

6.2.106. 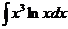6.2.107.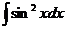

6.2.108. 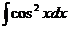6.2.109.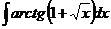

6.2.110. 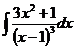6.2.111.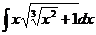

6.2.112. 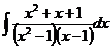6.2.113.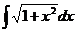

6.2.114.