Определитель матрицы. Вычисление определителей второго и третьего порядков. Свойства определителя
Определителем (детерминантом) матрицы А второго порядка
А = 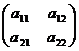
 называется число, равное разности попарных произведений элементов главной и побочной диагоналей:
называется число, равное разности попарных произведений элементов главной и побочной диагоналей: 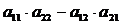 , т.е.
, т.е.
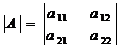 =
= 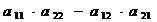 (6.1)
(6.1)
Определителем третьего порядка называется число, находимое по формуле:
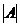 =
= 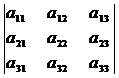 = =
= = 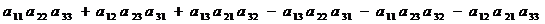 (6.2)
(6.2)
При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (правилом Сарруса):
«+» «-»














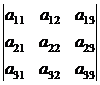
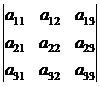 (6.3)
(6.3)
Определитель обозначают: 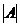 , D, det, Δ.
, D, det, Δ.
Пример. Вычислить определитель, пользуясь правилом треугольника
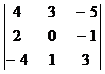 .
.
Решение. По формуле (6.3) получим
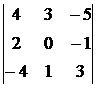 = 4∙0∙3 + 3∙(-1)∙(-4) + (-5)∙2∙1- (-5)∙0∙(-4) – 4∙(-1)∙1 – 3∙2∙3 =
= 4∙0∙3 + 3∙(-1)∙(-4) + (-5)∙2∙1- (-5)∙0∙(-4) – 4∙(-1)∙1 – 3∙2∙3 =
= 0 + 12 – 10 – 0 + 4 – 18 = -12.
Свойства определителя
1) Величина определителя не меняется, если заменить его строки соответствующими столбцами ( т.е. транспонирование):
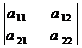 =
= 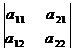 ;
;
2) Величина определителя не меняется, если к элементам к.-л. его строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на одно и то же число:
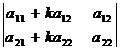 =
= 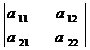 ;
;
3) Величина определителя меняет знак, если поменять местами его строки или столбцы:
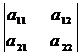 = -
= - 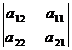 ;
;
4) Величина определителя увеличивается в k -раз, если элементы какого-либо его столбца или строки увеличить в k - раз, т.е. общий множитель, имеющийся в строке или столбце, можно выносить за знак определителя:
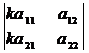 = k
= k 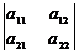 ;
;
5) Величина определителя равна нулю, если имеет две одинаковые строки (столбца);
6) Величина определителя равна нулю, если все элементы некоторой строки (или столбца) равны нулю.
7) Величина определителя равна нулю, если элементы 2-х строк (столбцов) пропорциональны;
8) Треугольный определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали, - нули, равен произведению элементов главной диагонали:
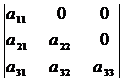 =
= 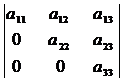 =
= 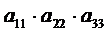 (6.4)
(6.4)
Формула Лапласа
Формула Лапласа позволяет понижать порядок заданного определителя. Для записи этой формулы необходимо ввести понятие минора и алгебраического дополнения элемента 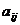 (i = 1,2,…, n; j = 1,2,…, n), расположенного на пересечении i-й строки и j-го столбца данного определителя.
(i = 1,2,…, n; j = 1,2,…, n), расположенного на пересечении i-й строки и j-го столбца данного определителя.
Если в данном определителе вычеркнуть элементы i-й строки и j-го столбца, то останется определитель, имеющий порядок на единицу меньше, чем данный. Этот определитель называется минором ( 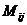 ) элемента
) элемента 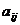 .
.
Алгебраическим дополнением 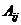 элемента
элемента 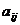 данного определителя называется минор
данного определителя называется минор 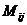 ,
,  взятый со знаком, соответствующим выражению
взятый со знаком, соответствующим выражению 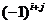 , т.е.
, т.е.
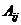 =
= 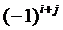
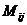 . (6.5)
. (6.5)
Формула Лапласа основана на том, что определитель можно представить в виде суммы произведений элементов всякой его строки (столбца) на их алгебраические дополнения. Этим данный определитель разлагается по элементам любой его строки (столбца), т.е.
разложение 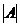 по элементам i–й строки:
по элементам i–й строки:
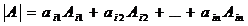 , (6.6)
, (6.6)
или разложение 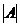 по элементам j–го столбца:
по элементам j–го столбца:
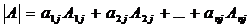 (6.7)
(6.7)
В частности, разложение определителя матрицы А третьего порядка по элементам первой строки имеет вид
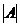 =
= 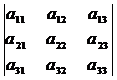 =
= 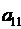 ·(-1)
·(-1) 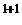
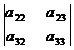 +
+ 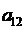 ∙(-1)
∙(-1) 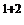
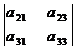 +
+
+ 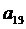 ·(-1)
·(-1) 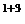
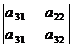 =
=
= 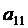 ·
· 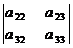 -
- 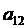 ·
· 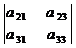 +
+ 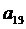 ·
· 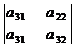 (6.8)
(6.8)
или
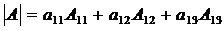 (6.9)
(6.9)
Пример. Вычислить определитель по формуле Лапласа:
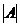 =
= 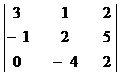 .
.
Решение. Разложим данный определитель по третьей строке, применяя формулу (2.6), при i = 3:
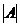 = 0 +(-4)∙(-1)
= 0 +(-4)∙(-1) 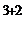
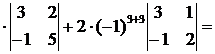 4 · (3 · 5 – 2 ∙ (-1)) +
4 · (3 · 5 – 2 ∙ (-1)) +
+ 2 · (3 ∙ 2 – 1 ·(-1)) = 4 · 17 + 2 ∙ 7 = 82.
