Обзор основной рекомендованной литературы

1. Высшая математика и математическая статистика : учеб. пособие / ред. Г.И. Попов. - 2-е изд. - М. : Физическая культура, 2007. - 368 с.

В учебном пособии изложены основные разделы линейной алгебры, аналитической геометрии, математического анализа, теории вероятностей и математической статистики; рассмотрены примеры решения типовых задач по всем разделам курса. Особое внимание в пособии уделено непараметрическим критериям статистики, которое получили интенсивное развитие в плане выработки новых критериев за последние годы. Содержание пособия соответствует государственному образовательному стандарту и программе по дисциплине «Математика»

Учебное пособие предназначено для студентов ВУЗов физической культуры.

2. Алексеева И.В. Элементы аналитической геометрии и векторной алгебры: методическое пособие для студентов вузов. Великие Луки, 2010. – 80 с.

В методическом пособии рассматриваются следующие темы: «Аналитическая геометрия на плоскости и в пространстве», «Векторная алгебра». В книге изложен теоретический материал, рассмотрены примеры решения основных типов задач, приведены задачи для самостоятельного решения, две расчетно-графические работы по темам «Аналитическая геометрия на плоскости» и «Элементы векторной алгебры и аналитической геометрии в пространстве», тесты для контроля знаний студентов. Изложение материала ведется методически строго и последовательно. Методическое пособие соответствует государственному стандарту.

Пособие предназначено для студентов и преподавателей высших учебных заведений физической культуры и спорта.

23. Гмурман В.Е. Теория вероятностей и математическая статистика: учеб.пособие для бакалавров/В.Е.Гмурман.-12-е изд. – М.: Изд.Юрайт; ИД Юрайт, 2012. – 479 с.: ил. – Серия: Бакалавр

Пособие содержит в основном весь материал программы по терии вероятностей и математической статистике. Большое внимание уделено статистическим методам обработки экспериментальных данных. В конце каждой главы есть задачи с ответами для контроля знаний.

Для студентов вузов и лиц, использующих вероятностные и статистические методы при решении практических задач.

МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

Перечень необходимых технических средств, оборудования, приборов для проведения основных форм учебного процесса:

для проведения лекционных занятий - специально оборудованная лекционная аудитория с мультимедийным проектором, экраном, ноутбуком, колонками (для демонстрации учебных видеороликов);

для проведения практических занятий - аудитория с доской

11. КАЛЕНДАРНО-ТЕМАТИЧЕСКИЙ ПЛАН лекций и практических занятий по дисциплине «Математика»

Первый курс, первый семестр

№ п/п	Дата проведения	Темы лекций и практических занятий	Перечень необходимого оборудования, наглядные пособия	Количество часов и вид занятия
		Прямоугольная и полярная системы координат. Простейшие задачи на плоскости. Прямая линия на плоскости	Мультимед	Лекция 1, 2ч
		Линии второго порядка	Мультимед	Лекция 2, 2ч
		Определение координат точки в разных системах координат. Переход от полярной системы координат к декартовой и наоборот. Решение простейших задач на плоскости, вычисление площадей треугольников. Различные виды уравнений прямой на плоскости.	Калькулятор, Справочник, материалы для граф.работ	Практич.1, 2ч
		Матрицы, определители 2-го и 3-го порядка. Решение систем линейных уравнений	Мультимед	Лекция 3, 2ч
		Угол между двумя прямыми,условия параллельности и перпендикулярности прямых, расстояние от точки до прямой.	Калькулятор, Справочник, материалы для граф.работ	Практич.2, 2ч
		Функция. Предел и непрерывность функции	Мультимед	Лекция 4, 2ч
		Приведение уравнений кривых второго порядка к каноническому виду и определение типа кривых, их основные характеристики и изображение этих кривых графически	Калькулятор, Справочник, материалы для граф.работ	Практич.3 2ч
		Производная и дифференциал	Мультимед	Лекция 5, 2ч
		Построение матриц. Вычисление определителей по схеме треугольников, по формуле Лапласа. Матричная запись системы линейных уравнений. Решение систем линейных уравнений методом Крамера.	сборник задач. Калькулятор	Практич.4, 2ч
		Приложение производной	Мультимед	Лекция 6, 2ч
		Контрольная работа № 1. «Элементы аналитической геометрии на плоскости и линейной алгебры»	Калькулятор, Справочник, материалы для граф.работ	Практич.5, 2ч
		Неопределенный интеграл	Мультимед	Лекция 7, 2ч
		Функция. Нахождение области определения и значения функции. Решение задач на четность, нечетность, периодичность функций. Нахождение обратных и сложных функций.	Калькулятор, сборник задач	Практич.6, 2ч
		Определенный интеграл	Мультимед	Лекция 8, 2ч
		Нахождение пределов функции. Раскрытие неопределенностей. Нахождение пределов функции с применением первого и второго замечательных пределов.	Справочник, сборник задач	Практич.7, 2ч
		Дифференциальные уравнения первого порядка с разделяющимися переменными. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами	Мультимед	Лекция 9, 2ч
		Нахождение производных элементарных и сложных функций. Дифференциал функций. Производные и дифференциалы высших порядков.	Справочник, сборник задач	Практич.8, 2ч
		Элементы теории вероятности	Мультимед	Лекция 10, 2ч
		Составление уравнений касательной и нормали к кривой. Нахождение скорости и ускорения прямолинейно движущегося тела с помощью производной. Приближенное вычисление наращенного значения функций с помощью дифференциала.	Таблицы, справочник, сборник задач	Практич.9, 2ч
		Правило Лопиталя. Исследование функций с помощью производной	Таблицы, справочник, сборник задач	Практич.10, 2ч
		Вычисление неопределенных интегралов с помощью метода разложения, подведения под знак дифференциала, подстановки, интегрирования по частям.	Таблицы, справочник, сборник задач	Практич.11, 2ч
		Вычисление определенного интеграла. Способы интегрирования.	Таблицы, справочник, сборник задач	Практич.12, 2ч
		Нахождение площадей с помощью определенного интеграла.	Таблицы, справочник, сборник задач	Практич.13, 2ч
		Контрольная работа № 2 «Предел функции. Производная функции. Неопределенный и определенный интегралы. Площадь криволинейной фигуры»	калькулятор, таблицы	Практич.14, 2ч
		Дифференциальные уравнения первого порядка с разделяющимися переменными. Задача Коши. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.	Калькулятор, Справочник, материалы для граф.работ	Практич.15, 2ч
		Решение задач с применением формул комбинаторики. Нахождение вероятностей совместных и несовместных событий, зависимых и независимых событий, появления хотя бы одного события. Нахождение условной и полной вероятности.	Таблицы, справочник, сборник задач	Практич.16, ч
		Случайные величины и их характеристики. Решение задач с применением формул Бернулли. Элементы мат.статистики.	Таблицы, справочник, сборник задач	Практич.17, 2ч

ПРИЛОЖЕНИЕ №1

Контрольные работы для студентов

КОНТРОЛЬНАЯ РАБОТА №1

ПО МАТЕМАТИКЕ

ТЕМА: «Элементы аналитической геометрии на плоскости и линейной алгебры»

Вариант 1

1. В декартовой прямоугольной системе координат построить точку А (3; -1) и определить ее полярные координаты.

2. Определить угол между двумя прямыми , . Сделать рисунок.

3. Найти координаты центра и радиус окружности

х² + у² – 8х + 6у + 21 = 0

4. Построить матрицу С = 2 (А + В)·В^Т , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 2

1. Определить расстояние между двумя точками А (2;7) и В (6;4). Сделать рисунок.

2. Составить уравнение прямой, проходящей через данные две точки А(-2;1) и В(3;4) . Сделать рисунок.

3. Найти полуоси, координаты фокусов и эксцентриситет эллипса

х² + 16у² = 16

4. Построить матрицу С = (А - В)·А + 3В , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 3

1. Вычислить площадь треугольника, вершины которого лежат в точках А (-1;1), В (2;3), С (6;1). Сделать рисунок.

2. Составить уравнение прямой, проходящей через точку М (3;7) перпендикулярно прямой . Сделать рисунок.

3. Найти полуоси, координаты фокусов и эксцентриситет гиперболы

4х² - у² = 16

4. Построить матрицу С = В· (В - А) +2А , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 4

1. Найти координаты точки, делящей отрезок АВ, где А(3;5) и В(1;-4), в отношении λ = . Сделать рисунок.

2. Составить уравнение прямой, проходящей через точку М (2;1) параллельно прямой 2x + 3y + 4 = 0. Сделать рисунок.

3. Найти координаты фокусов и уравнение директрисы параболы

а) у² = 6х ; б) х² = - 16у

4. Построить матрицу С = А·(2А + В) - В , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 5

1. В декартовой прямоугольной системе координат построить точку А (7; -3) и определить ее полярные координаты.

2. Определить угловой коэффициент k и отрезок b , отсекаемый на оси Оу прямой 5x + 3y + 2 = 0. Сделать рисунок.

3. Найти координаты центра и радиус окружности

х² + у² - 2х + 4у – 20 = 0

4. Построить матрицу С = 2А – (А + В)·В , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 6

1. Найти координаты точки, делящей отрезок АВ, где А(2;-4) и В(6;3), в отношении λ = . Сделать рисунок.

2. Найти расстояние от точки М (-1; 2) до прямой 4x -3y + 6 = 0. Сделать рисунок.

3. Найти полуоси, координаты фокусов и эксцентриситет эллипса

9х² + 25у² = 225

4. Построить матрицу С = А·(В + А)– 3А , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 7

1. Определить расстояние между двумя точками А (-3;4) и В (4;-3). Сделать рисунок.

2. Составить уравнение прямой, проходящей через точку М (-2;4) параллельно прямой . Сделать рисунок.

3. Найти полуоси, координаты фокусов и эксцентриситет гиперболы

х² - 4у² = 16

4. Построить матрицу С = А(А – В) –2 (А + В) , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 8

1. Вычислить площадь треугольника, вершины которого лежат в точках А (-2;1), В (3;4), С (1;2). Сделать рисунок.

2. Составить уравнение прямой, проходящей через точку М (-2;3) перпендикулярно прямой 6x -2y -1 = 0. Сделать рисунок.

3. Найти координаты фокусов и уравнение директрисы параболы

а) у² = -16х ; б) х² = 4у

4. Построить матрицу С = (А + В)·(2В – А) , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 9

1. В декартовой прямоугольной системе координат построить точку А (5; -6) и определить ее полярные координаты.

2. Определить угол между двумя прямыми , . Сделать рисунок.

3. Найти координаты центра и радиус окружности

х² + у² + 10х - 18у + 70 = 0

4. Построить матрицу С = 2 (А + В)·В^Т , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 10

1. Определить расстояние между двумя точками А (1;3) и

В (-2;6). Сделать рисунок.

2. Составить уравнение прямой, проходящей через точку

М (-1;5) перпендикулярно прямой . Сделать рисунок.

3. Найти полуоси, координаты фокусов и эксцентриситет эллипса

4х² + 9у² = 25

4. Построить матрицу С = (А - В)·А + 3В , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 11

1. Вычислить площадь треугольника, вершины которого лежат в точках А (3;-1), В (4;4), С (-5;2). Сделать рисунок.

2. Составить уравнение прямой, проходящей через данные две точки А(3;-4) и В(2;6) . Сделать рисунок.

3. Найти полуоси, координаты фокусов и эксцентриситет гиперболы

4х² - у² = 16

4. Построить матрицу С = В· (В - А) +2А , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 12

1. Найти координаты точки, делящей отрезок АВ, где А(2;6) и

В(-4;8), в отношении λ = . Сделать рисунок.

2. Составить уравнение прямой, проходящей через точку М (-5;8) параллельно прямой 7x -2y +5 = 0. Сделать рисунок.

3. Найти координаты фокусов и уравнение директрисы параболы

а) у² = 6х ; б) х² = - 16у

4. Построить матрицу С = А·(2А + В) - В , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 13

1. В декартовой прямоугольной системе координат построить точку А (2; -8) и определить ее полярные координаты.

2. Определить угловой коэффициент k и отрезок b , отсекаемый на оси Оу прямой 3x - 2y + 9 = 0. Сделать рисунок.

3. Найти координаты центра и радиус окружности

х² + у² + 10х + 2у - 10 = 0

4. Построить матрицу С = 2А – (А + В)·В , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 14

1. Определить расстояние между двумя точками А (4;6) и

В (-2;5). Сделать рисунок.

2. Составить уравнение прямой, проходящей через точку М (4;-5) перпендикулярно прямой 2x -7y +10 = 0. Сделать рисунок.

3. Найти полуоси, координаты фокусов и эксцентриситет эллипса

9х² + 25у² = 225

4. Построить матрицу С = А·(В + А)– 3А , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 15

1. Вычислить площадь треугольника, вершины которого лежат в точках А (5;-1), В (2;6), С (-3;-5). Сделать рисунок.

2. Составить уравнение прямой, проходящей через точку М (6;2) параллельно прямой . Сделать рисунок.

3. Найти полуоси, координаты фокусов и эксцентриситет гиперболы

х² - 4у² = 16

4. Построить матрицу С = А(А – В) –2 (А + В) , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Вариант 16

1. Найти координаты точки, делящей отрезок АВ, где А(-4;2) и

В(-3;6), в отношении λ = . Сделать рисунок.

2. Найти отрезки, отсекаемые на осях координат прямой

2x + 7y + 4 = 0. Сделать рисунок.

3. Найти координаты фокусов и уравнение директрисы параболы

а) у² = -16х ; б) х² = 4у

4. Построить матрицу С = (А + В)·(2В – А) , где

А= , В=

5. Решить систему уравнений методом Крамера (Δ вычислить по формуле Лапласа; Δ₁ , Δ₂ , Δ₃ - по схеме треугольников)

Контрольная работа № 2

ТЕМА: «Предел функции. Производная функции. Неопределенный и определенный интегралы. Площадь криволинейной фигуры»

Вариант 1

1. Вычислить пределы функций:

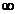а) , где а = 4; . б) .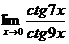

2. Найти производные функций: а) у = arccos ln x ; б) у =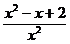

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) =

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: 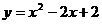, х = -1 , х = 2 и отрезком [-1;2] оси Ох.

Вариант 2

1. Вычислить пределы функций:

а) , a = 3 ; ∞ б)

2. Найти производные функций: а) у =sin ( ) ; б) у = (x+2)(2x ³- x)

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) = x + 3x - 9x – 6

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл: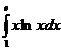

6. Вычислить площадь фигуры, ограниченной линиями: 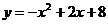, y = х + 6

Вариант 3

1. Вычислить пределы функций:

а) , a = 5 ; ∞ б)

2. Найти производные функций: а) у =cos³5x ; б) у =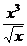

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) =2 x + 6x - 18x +120

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: 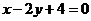, ,y = 0

Вариант 4

1. Вычислить пределы функций:

а) , a = 2 ; ∞ б)

2. Найти производные функций: а) у =sin ( 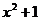) ; б) у =

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) =

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: , y = 0 , х = 3

Вариант 5

1. Вычислить пределы функций:

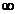а) , где а = 4; . б) .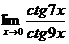

2. Найти производные функций: а) у = arccos ln x ; б) у =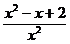

3.Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции

f(x) =

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: , х = - 4, х = - 2 , y = 0

Вариант 6

1. Вычислить пределы функций:

а) , a = 3 ; ∞ б)

2. Найти производные функций: а) у =sin ( ) ; б) у = (x+2)(2x³ - x)

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) = x + 3x - 9x – 6

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл: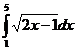

6. Вычислить площадь фигуры, ограниченной линиями: 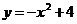, y = 0

Вариант 7

1. Вычислить пределы функций:

а) , a = 5 ; ∞ б)

2. Найти производные функций: а) у =cos³5x ; б) у =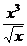

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) =2 x + 6x - 18x +120

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: ,

Вариант 8

1. Вычислить пределы функций:

а) , a = 2 ; ∞ б)

2. Найти производные функций: а) у =sin ( 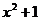) ; б) у =

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) =

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: , y = 0

Вариант 9

1. Вычислить пределы функций:

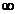а) , где а = 4; . б) .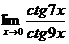

2. Найти производные функций: а) у = arccos ln x ; б) у =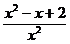

3.Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) =

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: 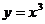, y = 8

Вариант 10

1. Вычислить пределы функций:

а) , a = 3 ; ∞ б)

2. Найти производные функций: а) у =sin ( ) ; б) у = (x+2)(2x ³- x)

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) = x + 3x - 9x – 6

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: , y = 0 , x = 1 , x = 3

Вариант 11

1. Вычислить пределы функций:

а) , a = 5 ; ∞ б)

2. Найти производные функций: а) у =cos³5x ; б) у =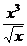

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) =2 x + 6x - 18x +120

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: , x = 1, x = 4 , y = 0

Вариант 12

1. Вычислить пределы функций:

а) , a = 2 ; ∞ б)

2. Найти производные функций: а) у =sin ( 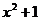) ; б) у =

3. Найти: а) интервалы возрастания, убывания функции;

б) максимум, минимум функции;

в) интервалы выпуклости, вогнутости, точки перегиба функции.

f(x) =

4. Найти неопределённый интеграл:

5. Вычислить определённый интеграл:

6. Вычислить площадь фигуры, ограниченной линиями: , y = 0

ПРИЛОЖЕНИЕ № 2

Расчетно-графическая работа

1. Дан треугольник АВС с вершинами А (m +1; n + 1), B ( m; -n) и С (-m; n).

Найти:

а) длину стороны треугольника АВ;

б) уравнение стороны АВ;

в) длину и уравнение медианы СМ;

г) длину и уравнение высоты СН;

д) угол АСВ;

е) площадь треугольника АВС;

ж) уравнение прямой , проходящей через вершину С и параллельной противоположной стороне;

з) точку пересечения медиан;

и) сделать чертёж.

Расчетно-графическая работа

1. Исследовать функцию и построить её график

Расчетно-графическая работа

2. Построить схематический чертёж и найти площадь фигуры, ограниченной линиями:

y = nx, y = 0, x = m

ПРИЛОЖЕНИЕ №3

Тексты лекций по математике

ТЕМА ЛЕКЦИИ №1: Прямоугольная и полярная системы координат. Простейшие задачи на плоскости. Прямая линия на плоскости

Система прямоугольных декартовых координат на плоскости.

Две перпендикулярные оси на плоскости с общим началом О и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости (рис.1.1). Координатную ось Ох называют осью абсцисс, ось Оу – осью ординат. Координатные оси разбивают плоскость на четыре четверти (рис. 1.2).

Прямоугольными декартовыми координатами точки М на плоскости называются расстояния от этой точки х = МL, у = МN до координатных осей Оу и Ох, взятые с соответствующими знаками. Декартовы координаты х и у точки М называются соответственно ее абсциссой и ординатой и символически обозначают так: М(х; у).

Для точек, лежащих на оси Оу, х = 0; для точек, лежащих на оси Ох, у = 0.

У У

II I

L х М

у x<0, y>0 x>0, y>0

О N Х

О Х

III IY

Рис 1.1 x<0, y<0 x>0, y<0

Рис. 1.2

Полярная система координат.

Пусть на плоскости даны некоторая точка О (назовем ее полюсом) и проходящая через нее ось ОР (назовем ее полярной осью) (рис.1.3). Положение любой точки М плоскости определяется расстоянием этой точки от полюса – радиус-вектором r и полярным углом φ между полярной осью и радиус-вектором r.

Две координаты (r, φ) определяют единственную

точку плоскости и называются ее полярными r М

координатами ( r 0, а 0 φ 2π).

Полюс О является точкой, радиус-вектор которой φ

равен нулю, а полярный угол φ не определен. О Р

рис. 1.3

Таким образом, системы координат позволяют установить

взаимно-однозначное соответствие между точками плоскости и парами чисел и наоборот.

Можно установить связь между декартовыми и полярными координатами одной и той же точки.<