Тема 7.2. Определенный интеграл
Лекция № 1(2 часа)
Понятие определенного интеграла. Свойства определенного интеграла. Основная формула интегрального исчисления. Замена переменной под знаком определенного интеграла. Интегрирование по частям. Площадь криволинейной фигуры.
Практическое занятие № 1(2 часа)
Вычисление определенного интеграла. Способы интегрирования.
Практическое занятие № 2(2 часа)
Нахождение площадей с помощью определенного интеграла.
Самостоятельная работа (6 часов)
Вычисление определенного интеграла. Нахождение площадей криволинейных фигур
с помощью определенного интеграла. Приближенное вычисление определенных интегралов. Решение задач.
Изучение темы направлено на приобретение:
знаний – основных теоретических положений, методов и приемов вычисления определенных интегралов, площадей криволинейных фигур.
умений – применять формулу Ньютона-Лейбница, различные методы вычисления определенных интегралов, строить чертежи искомых площадей фигур, ограниченных линиями, составлять и вычислять интегралы, соответствующие искомой площади;
навыков – применения знаний и умений при решении конкретных практических задач.
Раздел 8. Дифференциальные уравнения
Тема 8.1. Дифференциальные уравнения первого порядка с разделяющимися переменными. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Лекция № 1 (2 часа)
Понятие о дифференциальном уравнении. Дифференциальные уравнения первого порядка с разделяющимися переменными. Задача Коши. Линейные однородные уравнения второго порядка с постоянными коэффициентами.
Практическое занятие № 1(2 часа)
Дифференциальные уравнения первого порядка с разделяющимися переменными. Задача Коши. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Самостоятельная работа (4 часа)
Дифференциальные уравнения первого порядка с разделяющимися переменными. Задача Коши. Линейные однородные дифференциальные уравнения. Решение задач.
Изучение темы направлено на приобретение:
знаний – основных понятий о дифференциальном уравнении,
умений – решать дифференциальные уравнения, задачу Коши;
навыков – решения дифференциальных уравнений.
Раздел 9. Элементы теории вероятности и математической статистики
Тема 9.1. Элементы теории вероятности и математической статистики
Лекция № 1(2 часа)
Основные формулы комбинаторики. Элементы теории вероятности. Алгебра событий. Классическое определение вероятности. Свойства вероятности. Формула полной вероятности. Формула Бернулли. Понятие случайной величины. Закон распределения случайной величины. Математическое ожидание. Свойства математического ожидания. Дисперсия случайной величины, ее свойства.
Практическое занятие № 1 (2 часа)
Решение задач с применением формул комбинаторики. Нахождение вероятностей совместных и несовместных событий, зависимых и независимых событий, появления хотя бы одного события. Нахождение условной и полной вероятности.
Практическое занятие № 2 (2 часа)
Случайные величины и их характеристики. Решение задач с применением формул Бернулли. Элементы мат.статистики.
Самостоятельная работа (4 часа)
Решение задач по теории вероятности. Основные понятия комбинаторики. Случайные события. Классическое и геометрическое определение вероятности. Операции над вероятностями. Условная вероятность. Формула полной вероятности. Независимые повторные испытания. Схема Бернулли. Случайные величины и их характеристики. Плотность вероятности. Нормальное распределение. Элементы мат.статистики.
Изучение темы направлено на приобретение:
знаний – основных понятий и формул комбинаторики, основных понятий, методов, свойств, теорем и формул по теории вероятности и математической статистике
умений – применять полученные теоретические знания к решению типовых вероятностных и статистических задач;
навыков – проведения логических рассуждений, абстрагирования, решения практических задач, обработки полученных результатов научных исследований, проводить проверку статистических гипотез.
ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКОГО ОБЕСПЕЧЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
5.1. Перечень примерных контрольных вопросов для самостоятельной работы
1. Числовые множества. Операции над действительными числами
2. Комплексные числа.
3. Полярная система координат.
4. Прямая на плоскости
5. Плоскость в пространстве
6. Кривые второго порядка
7. Матрицы
8. Определители 2 и 3-го порядка
9. Формула Лапласа
10. Обратная матрица
11. Решение систем линейных уравнений методом Крамера
12. Решение систем линейных уравнений матричным методом
13. Решение систем линейных уравнений методом Гаусса
14. Векторы. Основные определения.
15. Линейные операции над векторами (сумма и разность векторов, умножение вектора на число).
16. Координаты вектора. Простейшие действия над векторами, заданными своими координатами. Длина вектора.
17. Скалярное произведение векторов и его свойства.
18. Векторное произведение векторов и его свойства
19. Переменная величина. Область ее определения.
20. Понятие функции. Область определения и область значения функции. Способы задания функции.
21. Ограниченность, монотонность, четность и периодичность функции. Возрастание и убывание функции. Обратная функция. Сложная функция.
22. Основные элементарные функции, их свойства и графики.
23. Непрерывность функции.
24. Предел функции
25. Производные и дифференциалы функций.
26. Приложение производной.
27. Методы интегрирования неопределенного интеграла
28. Вычисление определенных интегралов.
29. Площадь криволинейной фигуры.
30. Приближенное вычисление определенных интегралов.
31. Дифференциальные уравнения первого порядка с разделяющимися переменными. Задача Коши.
32. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
33. Элементы теории вероятностей.
34. Случайные величины. Закон распределения случайной величины. Характеристики случайных величин.
35. Элементы мат.статистики
5.2. Перечень примерных заданий для самостоятельной работы
1. Даны комплексные числа z1 = -3-3i , z2 = 1+4i. Найти сумму, разность, произведение и частное этих чисел, дать их геометрическую интерпретацию. Записать число z1 в тригонометрической форме .
2. В прямоугольной системе координат даны точки А(1; 1), В(0; 3), С(-1; 1), D(3; -6). Найти их полярные координаты.
3. В треугольнике с вершинами 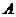 (−2; 1), В(1; −3), С(4; 3) определить:
(−2; 1), В(1; −3), С(4; 3) определить:
1) длины сторон;
2) уравнения сторон;
3) длины медиан;
4) уравнения медиан
5) точку пересечения медиан;
6) площадь треугольника;
7) внутренние углы треугольника;
8) длину высот треугольника;
9) уравнения высот треугольника;
10) уравнения прямых, проходящих через вершины треугольника, параллельно противоположным сторонам.
4. Определить параметры k и b прямых:
1) 3х – у + 2 = 0, 2) 5х – у + 3 = 0,
3) 3х +2 у = 0, 4) 2х +7 у = 0,
5. Найти отрезки, отсекаемые на осях координат прямыми:
1) 4х + у −8 = 0, 2) х – 2у + 6 = 0,
3) 3х − 2у + 5 = 0, 4) 6х + 2у + 3 = 0.
6. Вычислить угловой коэффициент k прямой, проходящей через две данные точки:
А(2; −5), В(3; 2)
7. Найти углы между прямыми: у = 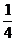 х – 3, х – 4у + 7 = 0
х – 3, х – 4у + 7 = 0
8. Указать, какие из следующих прямых параллельны и перпендикулярны:
1) 3х −15у + 16 = 0; 2) 3х + 15у −8 = 0;
3) 3х − у + 5 = 0; 4) 6х − 30у + 13 = 0;
5) х + 3у − 1 = 0; 6) 30х + 6у + 7 = 0;
7) 9х − 12у + 5 = 0; 8) 8х + 6у −13 = 0.
9. Дана прямая 5х + 3у −3 = 0. Определить угловой коэффициент k прямой:
1) параллельной данной прямой;
2) перпендикулярной к данной прямой.
10. Дана прямая 2х + 3у + 4 = 0. Составить уравнение прямой, проходящей через точку М(2; 1):
1) параллельной данной прямой;
2) перпендикулярной к данной прямой.
11. Составить уравнение плоскости, проходящей через точки А(0,1,0), В(3,0,-1), С (1, 2, 0).
12. Найти координаты центра и радиус окружности 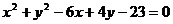 .
.
13. Составить простейшие уравнения эллипсов, зная что:
1) F 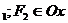 , его большая ось равна 10, а расстояние между фокусами 8;
, его большая ось равна 10, а расстояние между фокусами 8;
2) F 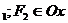 , его малая полуось равна 12, и эксцентриситет равен
, его малая полуось равна 12, и эксцентриситет равен 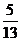 ;
;
14. Определить полуоси, координаты фокусов и эксцентриситет эллипсов:
1) 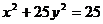 , 2) 9
, 2) 9 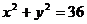 .
.
15. Составить простейшие уравнения гиперболы, зная что:
1) F 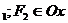 , расстояние между фокусами равно 10 и ось 2b = 8;
, расстояние между фокусами равно 10 и ось 2b = 8;
2) F 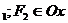 , расстояние между его фокусами равно 6, и эксцентриситет равен
, расстояние между его фокусами равно 6, и эксцентриситет равен 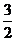 ;
;
16. Определить полуоси, координаты фокусов и эксцентриситет гипербол:
1) 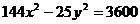 , 2) 9
, 2) 9 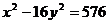 .
.
17. Составить уравнение параболы, зная, что:
1) парабола симметрична относительно оси Ох, проходит через точку М(−3; 6) начало координат;
2) парабола симметрична относительно оси Оу, проходит через точку М(6; 3) и начало координат.
18. Найти координаты фокуса и уравнения директрисы параболы, заданной уравнением: а) 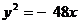 , б)
, б) 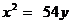 .
.
19. Найти произведения матриц А·В и В·А, если
а) А = 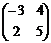 , В =
, В = 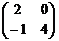 ; б) А =
; б) А = 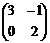 , В =
, В = 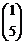 ;
;
в) А = 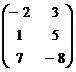 , В =
, В = 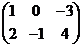 .
.
20. Построить матрицу С, выполнив указанные действия над заданными матрицами:
а) С = 2(А + В)·А -5 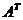 , где А =
, где А = 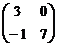 , В =
, В = 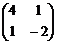 ;
;
б) С = 3А - А·В + 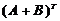 , где А =
, где А = 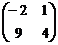 , В =
, В = 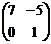 ;
;
21. Вычислить определители:
а) 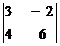 ; б)
; б) 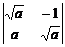 ; в)
; в) 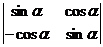 .
.
22. В следующих определителях найти все миноры и алгебраические дополнения элементов:
а) 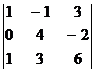 ; б)
; б) 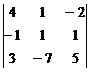 .
.
23. Вычислить определители: 1) по схеме треугольников;
2) по формуле Лапласа.
а) 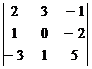 ; б)
; б) 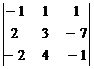 .
.
24. При каком значении λ матрица является вырожденной:
а) 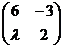 ;б)
;б) 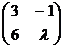 ; в)
; в) 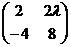 ; г)
; г) 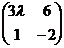 .
.
25. Найти обратные матрицы для матриц:
а) А = 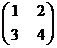 ; б) А =
; б) А = 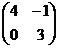 ;
;
26. Решить систему уравнений: а) методом Крамера;
б) матричным методом;
в) методом Гаусса.
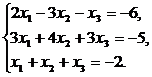
27. Дана точка О пересечения диагоналей параллелограмма АВСD и векторы 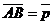 ,
, 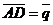 . Выразить векторы
. Выразить векторы 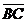 ,
, 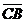 ,
, 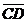 ,
, 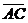 ,
, 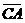 ,
, 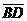 ,
, 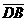 ,
, 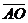 ,
, 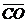 ,
, 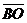 через
через 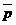 и
и 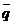 .
.
28. Даны векторы 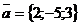 ,
, 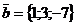 .Найти векторы:
.Найти векторы: 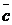 = 5
= 5 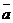 -2
-2 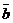 ,
, 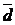 = 4
= 4 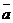 + 3
+ 3 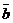 .
.
29. Найти скалярное произведение двух векторов 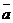 и
и 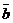 , для которых
, для которых 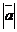 =6,
=6, 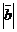 = 5 и угол между ними φ = 60°.
= 5 и угол между ними φ = 60°.
30. Даны два вектора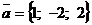 ,
, 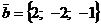 .Найти их скалярное произведение и угол между ними.Чему равно выражение
.Найти их скалярное произведение и угол между ними.Чему равно выражение 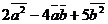 ?
?
31. Найти модуль векторного произведения двух векторов 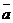 и
и 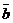 , для которых
, для которых 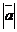 = 6,
= 6,
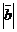 = 4 и угол между ними φ = 30°.
= 4 и угол между ними φ = 30°.
32. Даны векторы 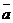 =
= 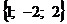 и
и 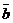 =
= 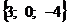 .Найти их векторное произведение, синус угла между ними и площадь параллелограмма, построенного на этих векторах.
.Найти их векторное произведение, синус угла между ними и площадь параллелограмма, построенного на этих векторах.
33. Найти область определения функции а) 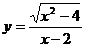 б) y=ln(x-3).
б) y=ln(x-3).
34. Вычислить пределы функций:
а) 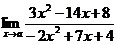 , где а = 4;
, где а = 4; 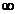 . б)
. б) 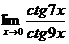 .
. 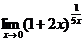
35. Найти производные функций: а) у = arccos ln x ; б) у = 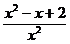 ;
;
в) у = (x+2)(2x 3- x) ; г) у = 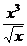 д) у =sin (
д) у =sin ( 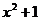 ) .
) .
36. Найти производные второго порядка от функций: а) у = ln 2x ; б) у = 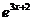
37. Найти уравнения касательной и нормали к кривой к кривой y = x 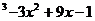 в точке М(1;6).
в точке М(1;6).
38. Найти предел, применяя правило Лопиталя: 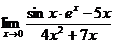
39. Исследовать на максимум и минимум функцию f(x)= 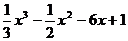 . Найти наибольшее и наименьшее ее значения на отрезке [0;3].
. Найти наибольшее и наименьшее ее значения на отрезке [0;3].
39. Исследовать функцию и построить ее график у = х3 – 3х.
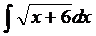 40.Найти неопределенные интегралы:
40.Найти неопределенные интегралы:
а) 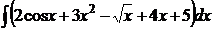 ; б)
; б) 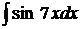 ; в)
; в) 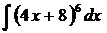 ; г) ; д)
; г) ; д) 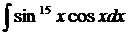 ; е)
; е) 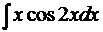
41. Вычислить определенные интегралы:
а) 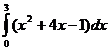 ; б)
; б) 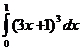 ; в)
; в) 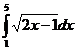 ; г)
; г) 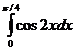 ; д)
; д) 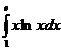
е) 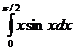
42. Вычислить площадь фигуры, ограниченной линиями:
1) 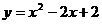 , х = -1 , х = 2 и отрезком [-1;2] оси Ох.
, х = -1 , х = 2 и отрезком [-1;2] оси Ох.
2) 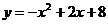 , y = х + 6
, y = х + 6
3) 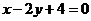 ,
, 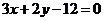 , y = 0
, y = 0
4) 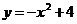 , y = 0
, y = 0
5) 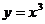 , y = 8
, y = 8
43. Проинтегрировать дифференциальное уравнение с разделяющимися переменными
(1+х2)dy – 2xydx = 0
44. Проинтегрировать дифференциальное уравнение 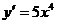 . Найти частное решение, удовлетворяющее условию: у = 1 при х = 0.
. Найти частное решение, удовлетворяющее условию: у = 1 при х = 0.
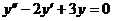 45. Найти решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами
45. Найти решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами
46. У продавца имеется 10 красных, 8 синих, 5 зеленых и 15 желтых шаров. Вычислить вероятность того, что купленный шар окажется красным, синим или зеленым.
47. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 200 руб., на 10 – по 150 руб., на 15 – по 100 руб., на 25 – по 20 руб. и на остальные – ничего. Найти вероятность того, что на купленный билет будет выигрыш не меньше 100 руб.?
48. Вероятность попадания в мишень при одном выстреле для данного стрелка 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах произойдет ровно два попадания в мишень.
49. Дискретная случайная величина задана рядом распределения
| Х | -2 | ||
| P | 0,3 | 0,1 | p3 |
Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Х.
50. Даны результаты измерения силы кисти студентов специализации «Борьба»:
42 42 43 44 44 44 45 45 45 46
48 48 48 49 50 50 50 51 53 53
54 55 55 58 60 60 65 68 68 72
Построить интервальный вариационный ряд (число интервалов k=6), гистограмму, полигон распределения.
51. В качестве оценки силовой подготовки семи учащихся 5 класса произведен тест на количество подтягиваний на перекладине. Данные теста следующие: 10, 9, 9, 8, 10, 9, 8. Вычислить моду, медиану, среднее арифметическое значение, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации и ошибку выборочного среднего данной выборки.
