Элементы теории вероятностей

МАТЕМАТИКА

(избранные главы)

для специальности

40.02.01 Право и организация социального обеспечения

Мурманск

Оглавление

Предел функции.. 4

Элементы комбинаторики.. 8

Элементы теории вероятностей.. 12

Дифференциальное исчисление.. 18

Интегральное исчисление. Неопределенный интеграл.. 24

Обыкновенные дифференциальные уравнения.. 34

Основы численных методов.. 39

ОСНОВЫ ДИСКРЕТНОЙ МАТЕМАТИКИ.. 45

Последовательности и ряды... 50

Предел функции

Вопросы к теме

1. Понятие предела функции. Свойства бесконечно больших и бесконечно малых функций. Теоремы о пределах.

2. Вычисления предела с неопределённостями типа .

Краткие теоретические сведения

Число А называется пределом функции при , если для любого можно указать такое , что для любого , удовлетворяющего неравенству , выполняется неравенство .

В этом случае пишут .

Функция называется бесконечно малой при , если

Функция называется бесконечно большой при , если

Свойства бесконечно малых и бесконечно больших функций:

1⁰. Если и - бесконечно малые при , то их сумма при также является бесконечно малой.

2⁰. Если бесконечно малая функция при , а ограниченная функция, то их произведение есть функция бесконечно малая.

3⁰. Если при функция имеет конечный предел, а функция - бесконечно большая, то

4⁰. Если - бесконечно малая функция при , то функция бесконечно большая и наоборот.

Теоремы о пределах:

Теорема 1. Если существуют пределы и при , то существует также и предел их суммы, равный сумме пределов функций и .

Теорема 2. Если существуют пределы и при , то существует также и предел их произведения, равный произведению пределов функций и .

Теорема 3. Если существуют пределы и при и то существует также и предел отношения, равный отношению пределов функций и .

.

Следствие 1. Постоянный множитель можно вынести за знак предела:

Следствие 2. Если , то

Следствие 3. Предел многочлена (целой рациональной функции) при равен значению этого многочлена при , т.е.

Следствие 4. Предел дробно-рациональной функции

при равен значению этой функции при , если принадлежит области определения функции, т.е.

Рассмотрим некоторые примеры.

Вычислить пределы:

1.1. 1.2. .

£ 1.1. По правилу нахождения предела многочлена находим

1.2.Так как при знаменатель дроби отличен от нуля, то по правилу нахождения предела дробно-рациональной функции получим

¢

2.1. 2.2. 2.3.

£ 2.1. Здесь предел делителя равен нулю: . Следовательно, теорему о пределе частного применить нельзя. Так как , то при есть величина бесконечно малая, а обратная ей величина – бесконечно большая. Поэтому при произведение есть величина бесконечно большая, т.е.

2.2. Здесь пределы числителя при равны нулю. Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, так как при получается отношение двух бесконечно малых величин.

Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и, следовательно, сделать возможным применение теоремы 3. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо. По определению предела функции аргумент 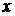стремится к своему предельному значению, никогда не принимая этого значения; поэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем

2.3. Пределы числителя и знаменателя при равны нулю: Разложим квадратный трехчлен в числители на линейные множители по формуле где и – корни трехчлена. Разложив на множители знаменатель, сократим дробь на Используя следствие 4, получим ¢

3.1. 3.2.

£ 3.1. Пределы числителя и знаменателя при равны нулю. Умножив числитель и знаменатель на сопряженный знаменателю множитель и затем сократив дробь на 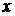, получим

3.2. Очевидно, что при функция представляет собой разность двух бесконечно больших величин. Выполнив вычитание дробей, получим дробь, числитель и знаменатель которой при стремится к нулю. Сократив дробь на , находим

¢

4.1. 4.2.

4.3. 4.4. 4.5.

£ 4.1. Первые три слагаемых при пределов не имеют, поэтому следствием 3 непосредственно воспользоваться нельзя. Вынося за скобки, получим

(при величины бесконечно малые и их пределы равны нулю).

При знаменатель неограниченно растет, т.е. является величиной бесконечно большой, а обратная величина бесконечно малой. Произведение бесконечно малой на ограниченную величину (постоянная – частный случай ограниченной величины) есть величина бесконечно малая, и предел ее при равен нулю. Следовательно,

4.3. При числитель и знаменатель – величины бесконечно большие. Поэтому при непосредственном применении теоремы 3 получаем выражение , которое представляет собой неопределенность. Для вычисления предела этой функции нужно числитель и знаменатель разделить на :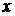

(при слагаемые величины бесконечно малые и, следовательно, их пределы равны нулю).

4.4. Разделим числитель и знаменатель на наивысшую степень аргумента в знаменателе, т.е. на :

При имеем и

Так как знаменатель есть величина ограниченная, то

4.5. При данная функция представляет собой разность двух бесконечно больших величин . Умножив и разделив функцию на выражение , получим

¢

Элементы комбинаторики

Вопросы к теме

1. Множества. Подмножества.

2. Понятие комбинаторики. Правила суммы и произведения.

3. Формулы комбинаторики: перестановки без повторений, размещения без повторений, сочетания.

Краткие теоретические сведения

Одним из фундаментальных, неопределяемых математических понятий является понятие множества. Множество можно представить себе как совокупность некоторых объектов, объединенных по одному какому-либо признаку (множество четных чисел, множество цветов спектра, множество букв русского алфавита).

Теория множеств создана великим немецким математиком Георгом Кантором. Главная заслуга Кантора состоит в признании того факта, что бесконечность – это не абстракция, придуманная философами, а реальность; что бесконечные совокупности предметов существуют наравне с конечными. В самом деле, легко построить прямоугольный треугольник с единичными катетами. По теореме Пифагора его гипотенуза равна , т.е. иррациональному числу, десятичное разложение которого бесконечно и не содержит периода.

Кантор описывает множество следующим образом: «Множество 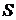есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества ».

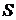Предметы (объекты), из которых составлено множество, называются элементами множества.

Если все элементы множества А являются в то же время элементами множества В, то множество А называется подмножеством множества В.

Студент должен понимать, что такое множество, уметь привести примеры, объяснить что означает конечное, бесконечное и пустое множество.

На практике часто приходится выбирать из некоторого множества объектов подмножества элементов, обладающих определенными свойствами, располагать элементы множества в каком-то определенном порядке, подсчитывать число всех возможных способов расположения некоторых предметов.

Так учителю приходится распределять некоторые различные виды работ между учащимися (или оценки); лингвисту – выбирать порядок слов в предложении; шахматисту – из нескольких серий ходов выбирать наилучшую.

В практической деятельности юристу часто приходится иметь дело с самыми разнообразными ситуациями. Умение анализировать сложившуюся обстановку, адекватно ее оценивать и делать правильные выводы является важным качеством каждого профессионала.

Задачи такого типа называются комбинаторными, поскольку в них речь идет о некоторых комбинациях работ, слов, ходов.

Область математики, в которой изучаются комбинаторные задачи называется комбинаторикой.

Другими словами, комбинаторика изучает количество комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества (конечные множества содержат конечное число элементов).

Комбинаторные задачи связаны: а) с выбором из некоторого множества элементов те, которые обладают заданными свойствами; б) с расположением этих элементов в определенном порядке; в) с расчетом числа возможных комбинаций.

Решение большинства комбинаторных задач основано на двух простых правилах: суммы и произведения.

Правило суммы. Пусть из множества А элемент можно выбрать способами, элемент - способом и т.д., элемент одним способом, отличными от предыдущих. Тогда выбор одного из элементов можно произвести способами.

Пример 1. Пусть в корзине имеется 7 апельсинов, 5 бананов и 10 яблок. Тогда выбор одного из фруктов можно сделать способами.

Правило произведения. Пусть А – некоторое множество, из которого выбор элемента можно осуществить способами, - способом и т.д., одним способом. Тогда одновременный выбор элементов в указанном порядке можно осуществить способом.

Пример 2. Пусть в велосипеде имеются 3 ведущие звездочки и 4 ведомые. Сколько передач имеется в велосипеде? £ Так как каждая передача определяется выбором одной ведущей и одной ведомой, то число всех передач совпадает с числом выборов одного элемента из 3 и другого элемента из 4. Поэтому ¢

Пример 3. Имеется 5 стульев и 2 студента. Сколькими способами можно посадить этих студентов на стулья? £ Первого студента можно посадить на стул пятью способами, а второго – четырьмя, т.к. один стул уже занят. Всего будет ¢

Рассмотрим наиболее употребительные формулы комбинаторики, которые используются при решении задач по теории вероятностей.

Перестановки без повторений

Перестановками без повторений называют комбинации, состоящие из одних и тех же 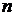различных элементов и отличающиеся только порядком их расположения.

Произведение 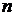натуральных чисел называют « факториал» и обозначают

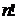
Другими словами, .

Например, и т.д. Для удобства принято, что и

Таким образом, обозначим число всех возможных перестановок, тогда .

Пример 4. Из четырех букв: a, b, c, d можно сделать 24 перестановки, так как Вот они:

abcd adbc bcda cabd dbac cdab

abdc adcb bcad cadb dbca cdba

acbd bacd bdac cbad dcab dabc

acdb badc bdca cbda dcba dacb

Пример 5. В отделении сержанта Сбруева проходят службу 5 новобранцев: Белкин, Пенкин, Свечкин, Овечкин, Мышкин. В свободное от нарядов время сержант обучает их, как рассчитываться по порядку. Сколько раз может Сбруев повторить это упражнение, используя только разные способы построения солдат?

£ Договоримся указывать порядок расположения солдат первыми буквами их фамилий. Например, БПСОМ, затем ПБСОМ и т.д. Все комбинации отличаются одна от другой порядком букв, значит ¢

Размещения без повторений

Размещениями без повторений называют комбинации, составленные из 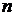различных элементов по элементов, которые отличаются либо составом элементов, либо их порядком. Обозначают и читают «размещения из 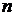по », причем .

Число всех возможных размещений: .

Отличие этих комбинаций состоит в том, что составление упорядоченного множества заканчивается, когда мы выберем элементов. Поэтому, чтобы найти число таких упорядоченных подмножеств, нужно перемножить чисел от 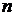до

Пример 6. Выбрать 3 краски из имеющихся пяти можно: способами.

Необходимо отметить, что перестановки являются частным случаем размещений.

Таким образом формулу размещений можно переписать иначе: .

Пример 7. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? £ Число таких флажков равно числу размещений из 6 по 2: ¢

Сочетания без повторений

Сочетаниями называют комбинации, составленные из 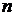различных элементов по элементов, которые отличаются хотя бы одним элементом. Обозначают: и читают «сочетание из 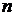по ».

Число сочетаний равно: .

Замечание. Сочетаниями являются неупорядоченными подмножествами данного множества, то есть в них не важен порядок расположения элементов, поэтому различные сочетания отличаются друг от друга составом элементов.

Свойства.

1⁰. 3⁰. 5⁰

2⁰. 4⁰.

Пример 8. Сколькими способами можно выбрать делегацию в 12 человек из группы в 20 человек? £ порядок следования в делегации не важен, поэтому способов выбора будет:

¢

Пример 9. Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей? £ ¢

Студент должен знать основные комбинаторные объекты (типы выборок), формулы и правила расчета количества выборок (для каждого из типа выборок); уметь: определять тип комбинаторного объекта (тип выборок), рассчитывать количество выборок заданного типа в заданных условиях.

Дифференциальное исчисление

Вопросы по теме

1. Понятие производной. Понятие дифференциала. Основные правила дифференцирования.

2. Дифференциальное исчисление нескольких переменных. Дифференциал функции.

3. Производной сложной функции.

4. Дифференциалы высших порядков.

Краткие теоретические сведения

Производнойфункции в точке называется предел отношения приращения функции в этой точке к приращению аргумента, когда последнее стремится к нулю: .

Функция , имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.

Для производной функции употребляются следующие обозначения: или . Нахождение производной называется дифференцированием.

Основные правила дифференцирования

Пусть - постоянная, 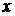- аргумент, - функции от 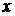, имеющие производные, тогда:

1. производная алгебраической суммы функций ;

2. производная произведения двух (трех) функций , ( );

3. производная произведения константы (постоянной) на функцию

;

4. производная частного (дроби)

; ; .

Если есть функция от : , где , в свою очередь, есть функция от 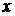: , т.е. если зависит от 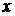через промежуточный аргумент , то называется сложной функцией от 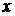(функцией от функции): .

Производная от сложной функции равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной:

, или .

При вычислении производных необходимо помнить, что:

и знать правила действий со степенями и корнями: m,n – любые числа

Таблица производных элементарных функций:

1 2 3 4

5 6 7 8

9 10 11

12 13 14

Примеры вычисления производной функции:

1. преобразуем функцию к виду , а затем воспользуемся правилом дифференцирования (3) и формулой (1) , получим

2.

3.

4.

используем правило нахождения производной произведения

5. используем правило нахождения производной частного

6.

1 способ: используем частный случай нахождения производной частного

2 способ: введем, отрицательный показатель

7. используем формулу (2), получаем:

8. заменим кубический корень дробным показателем

9.

10.

11.

12. для упрощения нахождения производной предварительно прологарифмируем дробь:

13. прологарифмируем дробь:

14.

15.

16. используем табличную формулу (3)

17.

18.

19.

20.

.

Дифференциальное исчисление нескольких переменных.

Дифференциал функции

Дифференциалом функции (дифференциалом I порядка) называется произведение производной этой функции на произвольное приращение аргумента : .

Дифференциал аргумента равен приращению аргумента . Поэтому дифференциал функции равен произведению производной этой функции на дифференциал аргумента: .

Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

Пусть и - дифференцируемые функции, которые образуют сложную функцию , тогда .

Таблица дифференциалов:

Пусть - дифференцируемые функции, - постоянная, 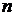- любое число.

1. ;

2. , в частности ;

3. , в частности ;

4. ;

5. (степенная функция);

6. (показательная функция),

в частности ;

7. (логарифмическая функция).

Примеры вычисления дифференциала функции:

1. ;

2. ;

3. ;

Дифференциалы высших порядков

Пусть - дифференцируемая функция, ее аргумент 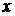- независимая переменная. Первый дифференциал есть также функция от переменной 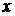. Можно найти дифференциал от этой функции.

Дифференциал от дифференциала функции называется вторым дифференциалом (или дифференциалом II порядка), обозначается: или . , аналогично .

Примеры вычисления дифференциалов функции:

1. Найти дифференциал II порядка .

2. Найти дифференциал III порядка .

Дифференциалы функций нескольких переменных

Пусть - дифференцируемая функция, , где и - частные производные.

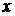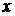Для нахождения частной производной по переменной достаточно заморозить на время «дифференцирования» и находить производную функции по переменной , на надо смотреть как на постоянную, и наоборот, при дифференцировании по надо считать постоянной .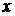

Примеры вычисления дифференциалов функции:

1.

2.

3.

Основы численных методов

Вопросы к теме

1. Абсолютная и относительная погрешности.

2. Округление чисел. Погрешности простейших арифметических действий

Краткие теоретические сведения

Приближенные значения величины

В процессе решения задач вычислитель сталкивается с различными числами, которые могут быть точными или приближенными. Точные числа дают истинное значение величины числа, приближенные – близкое к истинному, причем степень близости определяется погрешностью вычисления.

Например, в утверждениях: «на руке 5 пальцев», «в группе 32 студента», «куб имеет 6 граней» числа 5, 32, 6 – точные. В утверждениях: «ширина дома 14, 25 мм», «вес коробки 50 г», «в лесу около 5000 деревьев» числа 14,25; 50, 5000 – приближенные. Измерение ширины дома производится измерительными средствами, которые сами могут быть неточными; кроме того, измеритель при измерении допускает ошибку (погрешность). При взвешивании коробки также допускается ошибка, так как автоматические весы не чувствительны к увеличению или уменьшению веса на 0,5 г. Произвести точно подсчет количества деревьев в лесу невозможно, так как некоторые дерев