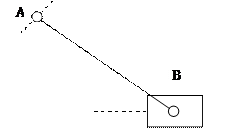
Структурный анализ механизма
Структурный анализ механизма
Присвоим номера звеньям, обозначим его кинематические пары и характерных точек Обозначим неподвижное звено (стойку) — 0, кривошип О А — 1, шатун АВ — 2, ползун В — 3. Центры масс звеньев обозначим буквой S с индексами, соответствующими номерам звеньев.
По формуле П. Л. Чебышева определим степень подвижности механизма:
W= Зп-2р5-р4,
где п — количество подвижных звеньев, п = 3;
p5 — число кинематических пар пятого класса, p5= 4;
p4 — число высших кинематических пар четвертого класса, p4= 0.
Подставив эти значения, получим W = 1. Это означает, что достаточно одному из звеньев задать движение, чтобы все остальные двигались синхронно. В нашем случае движение задано кривошипу ОА.
Выделим из состава механизма структурные группы Ассура, начиная с наиболее удаленной от ведущего звена, определяем их класс, порядок, вид. Результаты анализа заносим в табл. 1.
Таблица 1
Результаты структурного анализ
| № группы | Схема | Класс | Вид | Порядок | ||
| ||||||
| Механизм 1-го класса |
В целом рассмотренный механизм является механизмом 2-го класса, так как наивысший класс из рассмотренных групп — второй.
Кинематический анализ механизма
Для заданного положения механизма определим скорость и ускорения характерных точек, а также угловые скорости и ускорения звеньев.
Построение заданного положения механизма
План положения механизма строим в масштабе. Принимаем на схеме
О А =30 мм, получаем:
µ=lОА/ОА =0,09 /30 = 0,003 м/мм.
Остальные размеры вычисляем путем деления длин отрезков на масштаб.
Таблица 2
Геометрические размеры звеньев на схеме
| Обозначения | ОА | АВ | е |
| Размеры, мм |
По полученным значениям методом засечек построим заданное положение механизма.
Силовой расчет механизма
Определим силы, действующие на звенья механизма, для расчета деталей на прочность, износ, а также мощность двигателя, установить тип и размеры подшипников и т.д.
Силы, действующие на звенья механизма
Вычислим силы, действующие на механизм, и расставим их в соответствующих точках.
Силы тяжести найдем по формуле
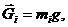
где mi — масса соответствующего звена;
g — ускорение свободного падения, g =9,82 м/с2 . При учебных
расчетах допускается принимать g = 10 м/с2 .
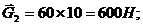
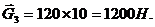
Силы тяжести прикладываются к центрам масс и направляются вертикально вниз.
Силы инерции звеньев вычислим из соотношения
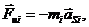
прикладываем к центрам масс и направим противоположно ускорениям соответствующих звеньев:
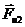 =
= 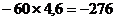 Н,
Н,
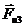 =
= 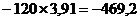 Н.
Н.
Моменты пары сил инерции вычисляются по формуле
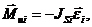
где JSi — момент инерции i-го звена, кг • м2.
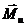 =
= 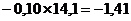 Н.
Н.
Сила полезных сопротивлений 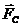 =3000 Н.
=3000 Н.
Расчет группы 2—3
Кинетостатический расчет начинают со структурной группы, наиболее удаленной от ведущего звена. Отделим от механизма группу звеньев 2- 3и заменим связи реакциями 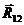 и
и 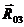 .
.
Разложим реакцию 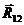 нанормальную и тангенциальную составляющие.
нанормальную и тангенциальную составляющие.
Запишем уравнение моментов для звена 4 относительно очки В и определим 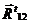 :
:
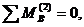
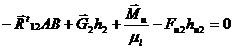 ,
,
где h2, hu2 — плечи действия сил (из чертежа), мм. Подставляем конкретные данные, получаем
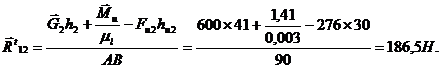
Запишем векторное уравнение равновесия для всей группы:
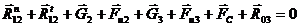
Это уравнение решим графически, для чего построим план сил в масштабе:
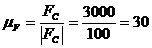 Н/мм.
Н/мм.
Тогда длины векторов будут равны:
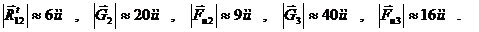
Построим многоугольник плана сил в масштабе 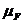 , замкнув его известными по направлениям векторами
, замкнув его известными по направлениям векторами 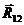 и
и 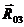 . Искомые величины равны:
. Искомые величины равны:
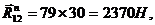
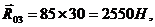
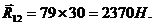
Для определения реакции 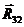 запишем векторное уравнение равновесия для звена 2:
запишем векторное уравнение равновесия для звена 2:
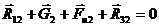
Из уравнения видно, что вектор 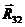 является замыкающим в системе сил, действующих на звено 2. Тогда величина этой реакции
является замыкающим в системе сил, действующих на звено 2. Тогда величина этой реакции
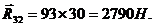
Таким образом, все неизвестные реакции в кинематических парах этой группы установлены.
Расчет ведущего звена
Ведущее звено 1 является механизмом 1-го класса и не относится к статически определимым группам ассура, т. е. оно не уравновешено.
Введем уравновешивающую силу FУ приложим ее в точку А и направим перпендикулярно к оси ОА. Кроме того, на ведущее звено действует реакция от звена 2 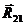 и реакция от неподвижного звена (стойки)
и реакция от неподвижного звена (стойки) 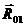 .
.
Для определения величины уравновешивающей силы составим уравнение моментов относительно точки О:
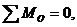
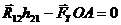 ,
,
откуда
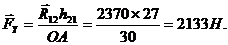
Запишем векторное уравнение равновесия для ведущего звена:
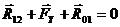
По этому уравнению построим план сил в масштабе.
Величина реакции 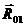
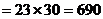 Н.
Н.
Проектирование механизма
Переведем фазовые углы в радианы:
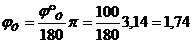 рад,
рад,
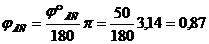 рад,
рад,
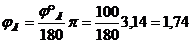 рад.
рад.
Рабочий угол кулачка составит:
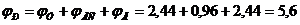 рад,
рад,
Примем по осям абсцисс кинематических диаграмм толкателя одинаковый масштаб 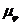 рад/мм. Тогда отрезки, отображающие фазовые углы на осях абсцисс, будут равны:
рад/мм. Тогда отрезки, отображающие фазовые углы на осях абсцисс, будут равны:
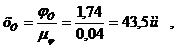
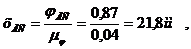

При параболическом движении толкателя (с постоянным ускорением) максимальное значение ускорения вычисляется по формуле
 ,
,
Скорость:
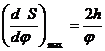 .
.
Используя эти формулы, вычислим максимальное значение ускорения и скорость толкателя при подъеме и опускания:
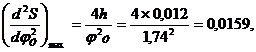
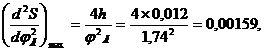
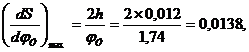
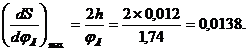
Приняв масштаб по осям ординат для всех диаграмм
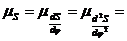 0.0002м/мм,
0.0002м/мм,
вычислим координаты
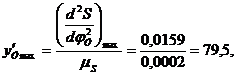
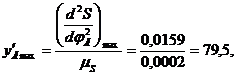
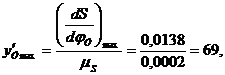
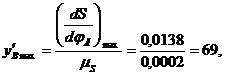
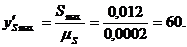
По вычисленным значениям построим диаграмму аналога ускорения. Для этого на оси абсцисс откладываем отрезки, отобрал фазовые углы, а по оси ординат — максимальные значения ускорения при подъеме и опускании.
С помощью графического интегрирования построим диаграмму аналога скоростей. Интегрирование диаграммы выполняется в порядке обратном графическому дифференцированию. На продолжении оси абсцисс влево от начала координат 02 откладываем полюсное расстояние Н2=Р2О2. Чтобы соблюсти принятый масштаб, вычислим величину полюсного расстояния по формуле
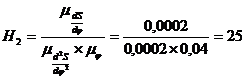 мм.
мм.
Проектируем на ось ординат точки 1", 2"и т. д. диаграммы аналога ускорений, проекции которых(точки а и b) соединяем с полюсом Р2.
Параллельно линии Р2b из начала координат О1 диаграммы аналогов скоростей проводим линию О14 до встречи с вертикалью, проведенной из точки 4 оси абсцисс. Из точки 4' проводим 4' — 8 параллельно Р2аи т. д.
Диаграмму перемещений можно построить двумя способами.
1. Метод графического интегрирования диаграммы аналога скоростей. Чтобы соблюсти принятый масштаб, величину полюсного расстояния вычислим по формуле
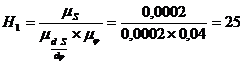 мм.
мм.
Из середины отрезков 01 -2, 2-4, 4-6 и т. восстанавливаем перпендикуляры до встречи с диаграммой аналога скоростей, а затем проводим горизонтальные линии до встречи с осью ординат. Полученные точки соединяем с полюсом Р1 . Параллельно линии Р1е из начала координат диаграммы перемещений 0 проводим линию 020 до встречи с вертикалью, восстановленной из точки абсцисс 2; из точки 20 проводим линию 2040, параллельную Р1f; източки 40 — линию 4060, параллельную Р1е, и т. д.
2. Аналитический метод. Диаграмма перемещения строится двух сопряженных ветвей парабол. Вершина одной параболы находится в начале координат, другой - в точке с координатами ( 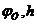 ). На оси ординат откладываем максимальный ход толкателя
). На оси ординат откладываем максимальный ход толкателя 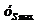 , а на оси абсцисс — фазовый угол удаления ху. Из середины отрезка ху восстановим перпендикуляр высотой
, а на оси абсцисс — фазовый угол удаления ху. Из середины отрезка ху восстановим перпендикуляр высотой 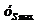 . Затем разделим его на то же число частей, что и отрезок, равный ху (на 8 частей). Из начала координат ху,
. Затем разделим его на то же число частей, что и отрезок, равный ху (на 8 частей). Из начала координат ху, 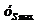 графика проводим лучи через точки 1у, 2у, 3у, 4у. Из точки с координатами ху,
графика проводим лучи через точки 1у, 2у, 3у, 4у. Из точки с координатами ху, 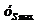 проводим лучи через точки 4у 5у 6у, 7у.Каждый луч, пересекаясь с одноименной ординатой дает точку, принадлежащую параболе.
проводим лучи через точки 4у 5у 6у, 7у.Каждый луч, пересекаясь с одноименной ординатой дает точку, принадлежащую параболе.
Аналогичным способом построим параболы и для фазы опускания толкателя. Для определения наименьшего радиуса профиля кулачка воспользуемся связью угла давления с размерами кулачка. Для этого путем графического исключения параметра 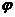 построим диаграмму функции
построим диаграмму функции
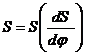
Проведем под углом 45° к оси абсцисс диаграмме аналогов скоростей наклонную линию ff. Из точек диаграммы аналогов скоростей проведем горизонтальные линии до встречи с наклонной, откуда проводим вертикальные линии до встречи с горизонтальными, проведенными из соответствующих точек диаграммы перемещений. Соединив полученные точки плавной кривой, получим диаграмму плеч. Проведем касательные к кривой под углом 30° к центру кулачка.
Точка пересечения касательных явится оптимальным геометрическим местом расположения центра вращения кулачка. Соединив последний с нулевым положением толкателя, получим величину минимального радиуса теоретического профиля кулачка Rmin.
Измерим минимальный радиус кулачка. Построим окружность минимального радиуса Rmin, разобьем эту окружность в соответствии с осью ординат. Из точек деления проведем дуги радиусами в центре окружности 0. На пересечении этих дуг с лучами, проходящими через точки деления окружности, принадлежащими профилю кулачка. Соединив все точки плавной кривой, построим теоретический профиль кулачка, уменьшив который на величину радиуса ролика 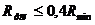 построим действительный профиль кулачка.
построим действительный профиль кулачка.
Синтез зубчатого механизма
Исходные данные:
т = 10 мм, z4 = 18, z5 = 25, i1H = 6.
Заключение
В данном курсовом проекте было произведено комплексное исследование на примере кривошипно-ползунного механизма, широко применяющегося в технике. Произведен структурный анализ механизма, кинематический анализ, силовой расчет. Рассмотрен синтез кулачкового механизма на примере проектирования механизма с поступательно движущимся толкателем. Изучен синтез зубчатого механизма на примере двухступенчатого редуктора.
Выполнены три чертежа формата А1, на первом чертеже представлен силовой анализ данного механизма. На нем представлен механизм, план скоростей, план ускорений, план сил, рычаг Жуковского. На втором чертеже профилирование кулачка с диаграммой аналога перемещений и диаграммой плеч. На третьем чертеже представлена картина эвольвентного зацепления.
Библиографический список
1. Артоболевский И.И. Теория механизмов машин/ И.И. Артоболевский. – М.: 1975.- 640 с.
2. Курсовое проектирование по теории механизмов машин/ Н.И. Наумкин , М.Н. Чаткин, В.Ф. Купряшкин и др.; под ред. П.В. Сенина, Н.И. Наумкина. – Саранск: Изд- во Мордов. ун-та,2003.- 332 с.
Структурный анализ механизма
Присвоим номера звеньям, обозначим его кинематические пары и характерных точек Обозначим неподвижное звено (стойку) — 0, кривошип О А — 1, шатун АВ — 2, ползун В — 3. Центры масс звеньев обозначим буквой S с индексами, соответствующими номерам звеньев.
По формуле П. Л. Чебышева определим степень подвижности механизма:
W= Зп-2р5-р4,
где п — количество подвижных звеньев, п = 3;
p5 — число кинематических пар пятого класса, p5= 4;
p4 — число высших кинематических пар четвертого класса, p4= 0.
Подставив эти значения, получим W = 1. Это означает, что достаточно одному из звеньев задать движение, чтобы все остальные двигались синхронно. В нашем случае движение задано кривошипу ОА.
Выделим из состава механизма структурные группы Ассура, начиная с наиболее удаленной от ведущего звена, определяем их класс, порядок, вид. Результаты анализа заносим в табл. 1.
Таблица 1
Результаты структурного анализ
| № группы | Схема | Класс | Вид | Порядок | ||
| ||||||
| Механизм 1-го класса |
В целом рассмотренный механизм является механизмом 2-го класса, так как наивысший класс из рассмотренных групп — второй.