Взаимное положение прямых линий.
Точка на прямой линии.
Взаимное положение прямых линий.
3. Проекции плоскостей. Классификация плоскостей по расположению в пространстве. Способы задания плоскостей общего и частного положений. Комплексные чертежи плоскостей общего и частного положений. Построение точки и прямой в плоскости. Прямые уровня в плоскости. Параллельность прямой и плоскости. Параллельность плоскостей.
Поверхности, образованные вращением прямой линии
1) цилиндр вращения – вращение прямой вокруг //-ой ей оси;
2) конус вращения – вращение прямой вокруг пересекающейся с ней оси;
3) однополосный гиперболоид вращения – вращение прямой вокруг скрещивающейся с ней оси.
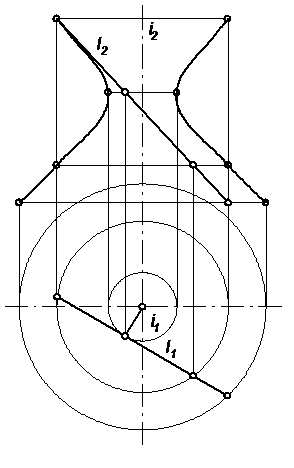
При вращении окружности
1) сфера;
2) тор – открытый, закрытый;
При вращении кривых
1) эллипса - эллипсоид вращения;
2) параболы – параболоид вращения;
3) гиперболы – гиперболоид вращения.
Линейчатые поверхности общего вида
Линейчатойназывается поверхность, образованная при движении прямой линии в пространстве по какому-либо закону. В зависимости от характера движения могут получаться различные виды поверхностей. В общем случае линейчатую поверхность можно получить при движении прямой линии по трём направляющим.
Пусть заданы 3 линии a, b, c, которые примем за направляющие линейчатой поверхности.
Возьмём на направляющей «а» т.А и проведём через неё пучок прямых, пересекающих направляющую «с». Эти прямые образуют коническую поверхность с вершиной в т.А. Направляющая «b» пересечёт эту коническую поверхность в некоторой т.В. Точки А и В будут определять прямую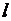 
, пересекающую направляющую «с» в т.С. Таким образом, взяв на направляющей «а» т.А, можно однозначно построить прямолинейную образующую линейчатой поверхности, проходящей через эту точку.
Перемещая т.А можно получить другие положения образующей и построить каркас поверхности.
Линейчатая поверхность, заданная таким способом называется косой цилиндр с 3-мя направляющими.
Если одна из направляющих – прямая, а две оставшиеся – кривые, то поверхность называется конусоид.
Если тремя направляющими являются прямые, то поверхность - однополосный гиперболоид.
Кроме указанного общего способа задания линейчатой поверхности существуют и другие способы, которые, путём наложения дополнительных ограничений, определяют закон движения прямолинейной образующей.
Цилиндрическая поверхность общего вида
Направляющая – кривая, прямолинейная образующая должна перемещаться // заданному направлению.
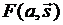 |  Если направляющая «а» замкнутая – цилиндр общего вида |
Точка на прямой линии.
Взаимное положение прямых линий.
3. Проекции плоскостей. Классификация плоскостей по расположению в пространстве. Способы задания плоскостей общего и частного положений. Комплексные чертежи плоскостей общего и частного положений. Построение точки и прямой в плоскости. Прямые уровня в плоскости. Параллельность прямой и плоскости. Параллельность плоскостей.