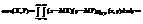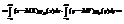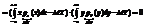Дисперсия (дискретной ) случайной величины.

Опр.: Пусть закон распределения случ. величины Х имеет вид:

Х:

Дисперсией D(X)- этой случ. величины называется число, вычисл. по ф-ле:

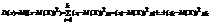хх этой случ. величины около её мат. ожидания.

Св-ва дисперсии: 1)D(С)=0, С- пост. случ. величина.

2)D(aX)=aв квадрате×D(X).

3)Пусть случ. величины X иY-независимы =>D(X±Y)=D(X)+D(Y). 4)D(X)=M(X в квадрате) – М в квадрате(Х).

5)Пусть случ. величины Х1,Х2,…Хn- независимы и D(X1)=…=D(Xn)=s в квадрате. ; тогда D((x1+…+xn)/n)=(s в квадрате)/n). Замечание: 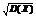– назыв. среднеквадратическим отклонением случ. величины X и часто обозначается черезs(сигма).

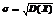Теорема: Пусть случ. величина Х биномиально распределена с параметрами n и p, тогда M(X)=np; D(X)=npq; q=1-p; M(X/n)=p; D(X/n)=(pq)/n.

Док-во: Пусть Х- число наступившего события А в nповторн. независ. исп-ях в каждом из которых соб А наступает с вер-тью р => Х=Х1+Х2+…+Хn,где Xi- число наступ-его соб-я А в i испытаний (1£i£n). Х1,Х2,…Хn– независ. и одинаково распределены. 1£i£ n.

M(Xi)=0×q+1×p=p. ; 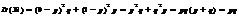M(X)=M(X1+…+Xn)=M(X1)+…+M(Xn)=p+…+p=np.

D(X)=D(X1+…+Xn)=D(X1)+…+D(Xn)=pq+..+pq=npq. Теорема доказана.

Пример: Пусть Х-бином. Распред-а n=3, p=0,8 ;M(X)=3×0,8=2,4 ; D(X)=3×0,8×0,2==0,48.

34.Основные числовые характеристики дискретных и непрерывных случайных величин: математическое ожидание, дисперсия и среднее квадратическое отклонение. Их свойства и примеры.

Математическим ожиданиемдискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности: М(Х) = х₁р₁ + х₂р₂ + … + х_пр_п .

Дисперсией (рассеянием)случайной величины называется математи-ческое ожидание квадрата ее отклонения от ее математического ожидания: D(X) = M (X – M(X))². (7.6)

Моменты случайной величины

Моме́нтслуча́йной величины́ — числовая характеристика распределения данной случайной величины. Определения

Если дана случайная величина Х определённая на некотором вероятностном пространстве, то:К-мнача́льным моментом случайной величины Х где 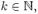называется величина 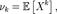если математическое ожидание 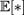в правой части этого равенства определено; К-м центра́льным моментом случайной величины называется величина

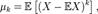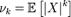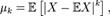К-м абсолю́тным и К -м центральным абсолютным моментами случайной величины называется соответственно величины и К-м факториальным моментом случайной величины Х называется величина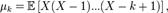

если математическое ожидание в правой части этого равенства определено.

Абсолютные моменты могут быть определены не только для целых k, но и для любых положительных действительных в случае, если соответствующие интегралы сходятся.

Ковариация .

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий используют и другие характеристики. К их числу относятся ковариация и коэффициент коррекции.

Опр. Ковариацией между случайными величинами Х и Y называется число 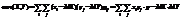, где 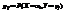.Для непрерывных случайных величин X и Y используют формулу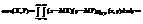 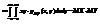. Покажем, что если случайные величины Х и Y независимы, то 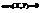. Пусть Х и Y—непрерывные случайные величины