Обобщенные силы и перемещения.

Упругие системы.

Линейные системы.

Матрицы жесткости и податливости.

Принцип суперпозиции.

Простейшая линейная упругая система. Потенциальная энергия.

Теоремы взаимности работ и перемещений.

Потенциальная энергия линейной упругой системы, загруженной произвольным числом обобщенных сил.

Теорема Лагранжа и теорема Кастильяно.

Удельная работа напряжений.

Потенциальная энергия упругого тела.

Соотношения между напряжениями и деформациями и12. Соотношения между напряжениями и деформациями и потенциальная энергия линейного упругого тела.

Закон Гука для изотропного упругого тела.

Термомеханические системы. (Это из термодинамики)

Обобщенные силы и перемещения

Линейные упругие системы и их свойства .

Обобщенные силы и перемещения.

Обобщенными перемещениями называют любые величины, характеризующие изменение геометрии деформируемой механической

системы.

Обобщенной силой, соответствующей Q_i данному обобщенному перемещению q_i, называют фактор, определяющий элементарную работу dA, совершаемую над механической системой на приращении обобщенного перемещения dq_i:

dW = Q_i dq_i (1)

или

dW = Q_i dq_i, (1а)

если dW – возможная (виртуальная) работа, совершаемая на возможном (виртуальном)перемещении dq _i.

Пример. Для балки, изображенной на рис.1, в качестве обобщенных перемещений выберем вертикальные перемещения точек А и В и угол поворота сечения С:

q₁ = v_A, q₂ = v_B , q₃ = q_C ,

тогда соответствующими обобщенными силами будут вертикальные силы P_А и P_В, приложенные в точках А и В, и момент пары сил М_с, приложенной в сечении С. Эти обобщенные силы могут иметь любые вещественные (в том числе и нулевые) значения.

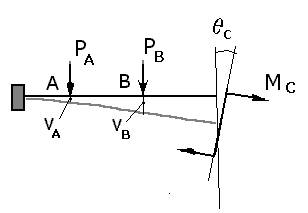
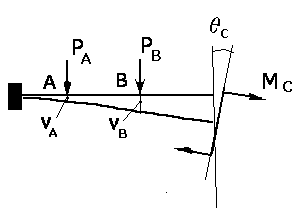
Рис.1 Обобщенные силы, действующие на балку и соответствующие им обобщенные перемещения.

Упругие системы.

Деформируемая система называется упругой (идеально упругой), если действующие на нее обобщенные силы связаны с обобщенными перемещениями взаимно однозначными зависимостями.

Обобщенные перемещения упругой системы зависят только от текущих значений обобщенных сил и не зависят от последовательности приложения и закона изменения их во времени.

Обобщенные перемещения упругой системы принято отсчитывать от исходного ненагруженного состояния. После полной разгрузки обобщенные перемещения возвращаются к начальным нулевым значениям: упругие деформации при полной разгрузке системы исчезают.

Линейные системы.

Деформируемая система называется линейной упругой (линейно-упругой), если обобщенные перемещения и силы связаны линейными зависимостями.

Линейную зависимость между силами и перемещениями принято называть законом Гука (обобщенным законом Гука).

Линейные упругие системы следуют закону Гука.

Пусть состояние линейно упругой деформируемой системы характеризуется n обобщенными перемещениями q_i, которым соответствуют обобщенные силы Q_i , (i=1,2,...,n).

Линейная зависимость каждого обобщенного перемещения от всех обобщенных сил выражается соотношениями:

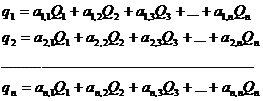
(2)

или, то же самое:

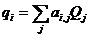, i,j = 1,2,..,n. (2а)

Постоянные коэффициенты а_i,j называются коэффициентами податливости упругой системы.

Чем больше коэффициент податливости a_i,j, тем большее перемещение q_i, вызывается обобщенной силой Q_j.

Нагрузим упругую линейную систему силой Q_j =1, полагая, что все остальные силы равны нулю. Тогда из(2) следует:

q_i = a_ij.

Коэффициент податливости a_ij равен i-тому обобщенному перемещениюq_i, вызванному единичной j-той обобщенной силой Q_j =1.