Методы решения л.д.у. первого порядка.

1. Метод вариации постоянной.

А. Находим общее решение однородного уравнения .

Перепишем однородное уравнение в виде уравнения с разделенными переменными

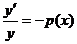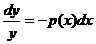, . Интегрируем правую и левую часть уравнения, получим

., .

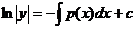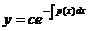Это будет общее решение однородного уравнения: .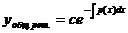

В. Подставляем это решение в неоднородное уравнение , но при c=с(x).

Дифференцируем y и подставляем в неоднородное уравнение.

Решаем полученное уравнение и находим с(x).

Полученное выражение для с подставляем в .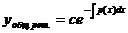

В общем виде решение неоднородного уравнения запишется так:

.

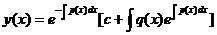Пример. , p(x)=3, q(x)=e .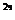

A. , , ,

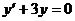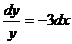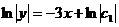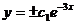
или 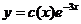, где c= .

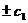В. 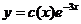, берем производную .

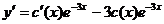Подставляем выражения для y и в уравнение .

Получим дифференциальное уравнение относительно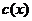

.

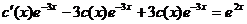Производим действия и получаем 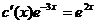или ,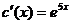

отсюда .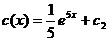

Это выражение подставим в = .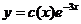

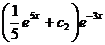Решение исходного уравнения: .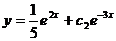

Метод подстановки.

Найти общее решение уравнения .

Положим

Подставим эти выражения в исходное уравнение:

.

Или (*)

Потребуем (или выберем u(x) такое), чтобы .

Найдем u(x) из уравнения , применив метод разделяющих переменных. Получим , .

Выберем какое-нибудь частное решение (например, при с=1) ,

подставим в (*), получим .

Найдем общее решение этого уравнения .

Общее решение исходного уравнения имеет вид: , где

- частное решение исходного уравнения,

- общее решение исходного уравнения.

Замечание . При решении уравнения методом разделенных переменных может быть потеряно решение , т.е. утеряны интегральные кривые . Поэтому получив методом разделенных переменных общее решение уравнения, нужно проверить, все ли частные решения мы охватили при подходящем значении с. В случае отсутствия, их нужно включить.

Пример (потеря решения).

.

Для удобства положим .

Тогда . .

Но исходное уравнение имеет решение у=0, которое не входит в запись . Поэтому запишем решение как , где с может быть равным нулю.

Итак, получив общее решение, необходимо проверить, входит ли в его состав при подходящих числовых значениях параметра с упомянутые частные решения. Если не входят, то нужно включить.

Пример (на метод подстановки). .

Положим .

Потребуем .

.

Выберем какое-нибудь частное решение этого уравнения .

Подставим это решение в (*): ,

найдем общее решение методом разделения переменных

.

Отсюда или .

Неполные д.у.первого порядка

Определение. Д.У. первого порядка 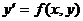называется неполным, если функция 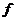явно зависит только от одной переменной: либо от 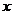, либо от .

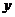1. .

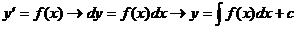2. 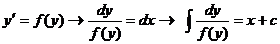. Методом разделения переменных определяется неизвестная функция (или ).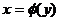

Уравнение 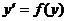называется автономным Д.У., такие уравнения имеют место в теории математического моделирования. Особый интерес представляют так называемые точки равновесия, или стационарные точки: нули функции 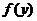, где 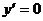.