Угловой скорости твердого тела

Тело H массой m₁ вращается вокруг вертикальной оси z с постоянной угловой скоростью ω₀; при этом в точке О желоба АВ тела H на расстоя­нии АО от точки А, отсчитываемом вдоль желоба, находится материаль­ная точка К массой т₂. В некоторый момент времени (t = 0) на систему начинает действовать пара сил с моментом M_z = M_z(t). При t=τ действие сил прекращается.

Определить угловую скоростью, тела H в момент t=τ.

Тело H вращается по инерции с угловой скоростью ω_τ

В некоторый момент времени t_t — 0 (t₁ — новое начало отсчета времени) точка К (самоходный механизм) начинает относительное движение из точки О вдоль желоба АВ (в направлении к В) по закону OK = s = s (t₁).

Определить угловую скорость сот тела Я при t₁ = Т.

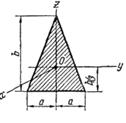
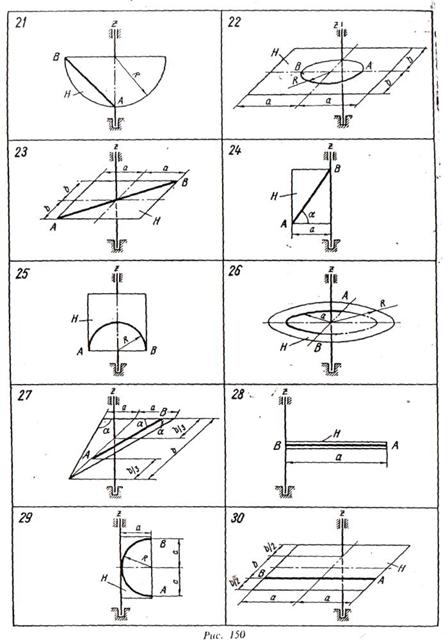
Тело Я рассматривать как однородную пластинку, имеющую форму, показанную на рис. 148 — 150. Необходимые для решения данные при­ведены в табл. 45 — 46. Таблица 45

№ вар	m1	m2	ω0 рад/с	a м	b м	R м	α град	AO м	Mz=Mz*(t) Н м	τ с	OK=s=s(t1)	T с
кг
			-1		1,5	1,2	-	πR/6	-29.6t2		(5 πR/12)t1
			-2	-	-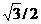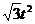
					-	-			-120t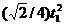
			-3	-	-		-	0.4	21t		0.6t1
			1,5		1,5	-	-		15	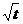	0.5t1	2.5
			-1,25	1,5	-	2,5	-	πa/6	-700t		(5 πa/18)t12
			-2	1,6		0,8	-				(πR/2)t12
				1,2	-			πa/2	240	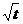	(πa/4)t1
				1,2	-	0,4	-	πR/4	-29.2t		(3 πR/4) t12
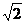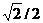						-			-90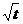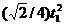
			-1		-	-	-		40t		0.4 t12
			-3		-		-		50t2		(πa/3)t1
					-	-	-	0.5	-27	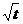	0.3t1
				-	-		-		120t		0.5t1
			-4		-				330t2		(πa/2) t12
			-5		1,2	-		0.4			0.3 t12
			-2	-	-	1,6	-	0.6	69t		0.6t1
						0,8	-	πR/2			(πR/8) t12
				1,5	-	-	-		-135t		(πa/4)t12
					-	1,2	-	πa/6	-14t2		(πa/12)t12
			-6	-	-		-		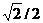75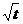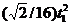
			-1	1,6	1,2	0,6	-	πR/2			(πR/2)t12
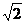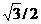						-	-		-210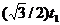
			-3	0,6	-	-		0.2	27t2		0.4t1
			-5	-	-	0,5	-		20t		(πR/6)t12
			-4	1,5	-		-	πa/6	1170	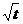	(πa/2)t12
					-	-			-25t		t12
			-2	0,6	-	-	-	0.1	5.6t		0.4)t1
				0,6	-	0,6	-		-6.3	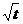	(5 πR/6)t1
				1,6	1,2	-	-	1.6	652t		0.2)t12

Примечание знак минус перед M_z и ω соответствует направлению вращения часовой стрелки, если смотреть со стороны положительного направления оси z

Т а б л и ц а 46 Осевые моменты инерции однородных пластинок

	Jx	Jy	Jz

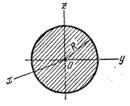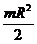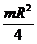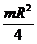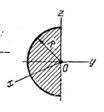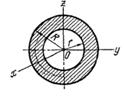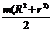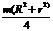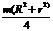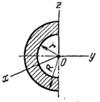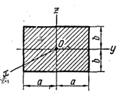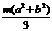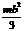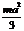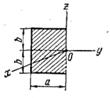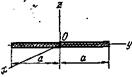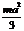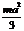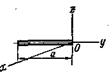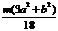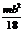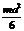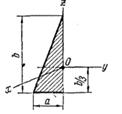Пример выполнения задания(рис. 151). Дано: m₁ = 200 кг; т₂ =80 кг; М_z = 592t Н • м; ω₀ = -2 рад/с; АО = 0,8 м; R = 2,4 м; а = 1,2 м; t = τ = 4 с; OK =5 = 0,5t₁²м; t₁= T=2с.

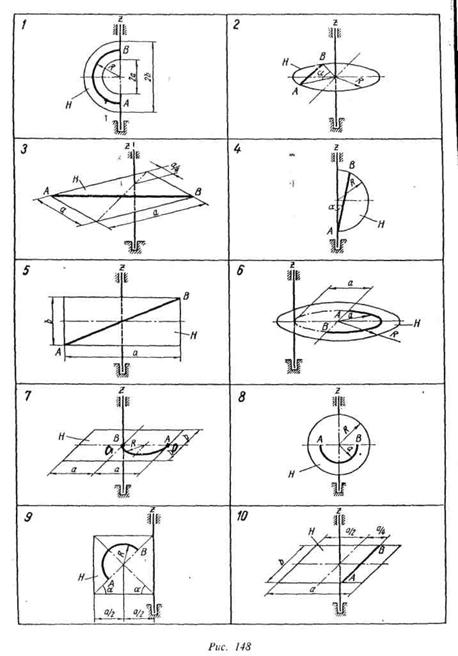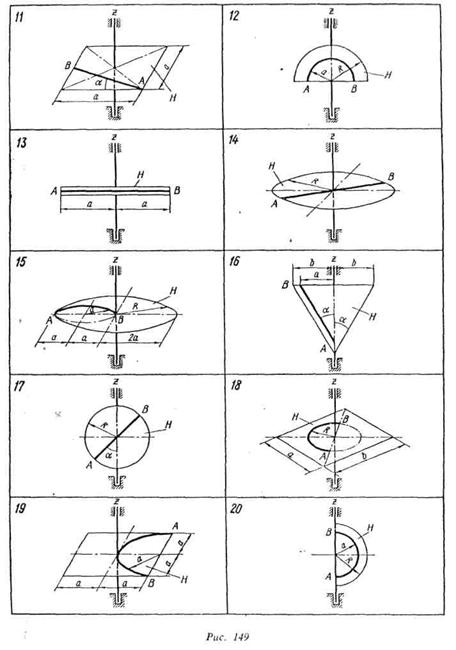
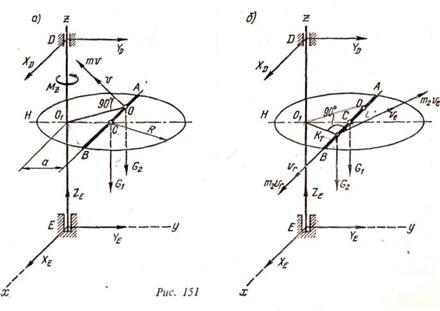Определить ω_τ и ω_T, считая тело H однородной круглой пластинкой. Решение. К решению задачи применим теорему об изменении кине­тического момента механической системы, выраженную уравнением

dL_z/dt =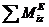

гдеL₂ — кинетический момент системы, состоящей в данном случае из тела Я и точки К, относительно оси z; 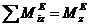— главный момент внешних сил, приложенных к системе, относительно оси z.

На систему за время от t = О до t = τ действуют силы: вес 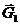тела H, вес 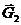точки К, пара сил с моментом М_г и реакции подпятника и подшипника (рис. 151, a).

Предположим, что вращение тела H происходит против вращения часовой стрелки, если смотреть со стороны положительного направления оси z; будем считать это направление положительным при определении знаков кинетических моментов.

Найдем выражение кинетического момента L_z системы, который скла­дывается из кинетического момента тела 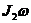и момента количества дви­жения точки К, находящейся в точке О тела H и имеющей скорость

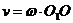
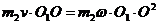
Таким образом,

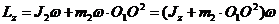
Главный момент внешних сил равен вращающему моменту М_г, так как другие силы момента относительно оси z не создают.

Уравнение, выражающее теорему об изменении кинетического момента, примет вид

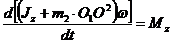(1)

где М_г = ct (с = 592 Н • м/с).

Разделим в уравнении (1) переменные и проинтегрируем левую и пра­вую части уравнения:

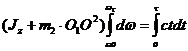
Тогда

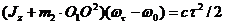(2)

Найдем числовые значения входящих в уравнение (2) величин.

Момент инерции тела Я относительно оси z найдем, используя теорему о зависимости между моментами инерции относительно параллельных осей:

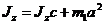
где J_:c — момент инерции тела Н — однородной круглой пластинки отно­сительно вертикальной оси, проходящей через центр масс тела параллель­но оси z:

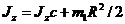
Тогда

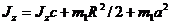
т. е.

J_z = 864 кг • м².

Из чертежа (рис. 151, б) находим

(O₁O)² = (ОС)² + (O₁ C)², или (О₁O )² = 4 м²,

поэтому

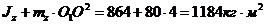
Таким образом, из уравнения (2)

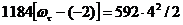
имеем

ω_τ= 2 рад/с.

После прекращения действия момента М_г тело Н вращается по инер­ции с угловой скоростью со,; при. этом к системе приложены силы 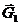, 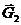реакции подпятника и подшипника (рис. 151,6).

Те же внешние силы действуют на систему и в течение промежутка времени от t_t = 0 до f_x = Т. при движении самоходной телега*.

Уравнение, выражающее теорему об изменении кинетического момента системы, имеет для этого периода времени вид

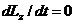
т. е.

L_z = const.

Определим значения кинетических моментов L_z0 при t₁=0 и L„ при f, = Т и приравняем эти значения.

Для t₁ = 0

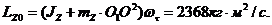
При t₁ > 0 скорость точки X складывается из относительной скорости 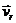по отношению к телу H и переносной скорости 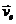в движении вместе с телом H. Поэтому для t₁ = T покажем два вектора количества движе­ния точки: m₂ 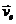, и m₂ .

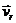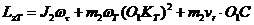Для t₁=T

Найдем

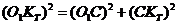
где

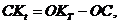
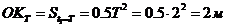
т. е.

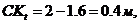
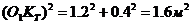
Относительная скорость

v_r = ds/dt = t₁, при t₁ = Т = 2 с.

v_r = 2 м/с.
Поэтому

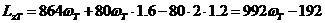
Приравнивая L_z0 и L_:T:

2368 = 992ω_T - 192,

находим,

ω_T = 2,59 рад/с.

Задание Д. 10. Применение теоремы об изменении кинетической энергии к изучению движения механической системы

Механическая система под действием сил тяжести приходит в движе­ние из состояния покоя; начальное положение системы показано на рис. 152-354. Учитывая трение скольжения тела 1 (варианты 1 — 3, 5, 6, 8 — 12, 17 — 23, 28 — 30) и сопротивление качению тела 3, катящегося без скольжения, (варианты 2, 4. 6-9, 11, 13-15, 20, 21, 24. 21, 29). пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастя­жимыми, определить скорость тела 1 в тот момент, koi ja пройденный им путь станет равным s.

В задании приняты следующие обозначения; m₁ m₂ m₃ m₄,— массы тел 1,2, 3, 4; R₂, r₂, R₃, r₃ — радиусы больших и малых окружностей; 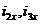— радиусы инерции тел 2 и 3 относительно горизонтальных осей, проходящих через их центры тяжести; α, β — углы наклона плоскостей к горизонту; f –коэффициент трения скольжения; δ – коэффициент трения качения

Необходимые для решения данные приведены в таблице 47. Блохи

Таблица 47

	m	3m	m	-				-		-	0.15	-	0.2 π	Массой водила пренебречь
	m	1/4m	1/10m	m		-		-		-	0.15	-	1.5
	m	2m	20m	-				-		-	0.10	0.20	0.2 π	Массами звеньев АВ, ВС и ползуна В пренебречь
	m	m	2m	-				-			0.20	0.32	1.2
	m	1/2m	1/4m	-			-	-		-	0.17	-	0.1 π	Массой водила пренебречь
	m	1/10m	1/10m	4/5m		-		-		-	0.10	-
	m	20m	20m	-				-	-	-	-	0.60	0.08 π	Массами звеньев АВ, ВС и ползуна В пренебречь
	m	1/4m	1/4m	-			-	-	-	-	-	-	0.04 π	Массой водила пренебречь
	m	m	m	1/3m		-		-	-	-	-	-	0.6 π	Массы и моменты инерции блоков 2 и 5 одинаковы Шатун 3 рассматривать как тонкий однородный стержень
	m	6m	6m	1/2m				-		-	-	0.20
	m	3m	3m	-		-		-		-	0.10	-	0.1 π	Шатун 3 рассматривать как тонкий однородный стержень
	m	1/4m	1/8m	-	-		-	-			0.20	0.20	2.4
	m	1/2m	3/10m	3/2m						-	0.12	-

№ вар	m1	m2	m3	m4	R2	R3	i2x	i2ε	α	β	f	δ см	s м	Примечание
кг	см	см	град
	m	4m	1/5m	4/3m	-	-	-	-		-	0.10	-
	m	1/2m	1/3m	-	-		-				0.22	0.20
	m	m	1/10m	m	-	-	-	-		-	0.10	-
	m	2m	40m	m				-	-	-	-	0.30	0.1π	Массами звеньев АВ, ВС и ползуна В пренебречь
	m	2m	m	-				-		-	0.12	-	0.28 π	Массой водила пренебречь
	m	3m	m	-	-		-	-			0.10	0.28	1.5
	m	2m	2m	-				-		-	-	0.20
	m	1/2m	1/3m	-	-		-	-			0.15	0.20	1.75
	m	2m	9m	-	-		-			-	0.12	0.25	1.5
	m	1/4m	1/4m	1/5 m	-	-	-	-		-	0.10	-
	m	1/2m	1/4m	-	-		-				0.17	0.20	2.5
	m	1/2m	1/5m	m		-		-		-	0.20	-	2.5
	m	2m	5m	2m				-		-	-	0.24
	m	1/2m	5m	4m	-		-	-	-	-	-	0.20		Массы 4-х колес одинаковы
	m	1/2m	4m	1/2m				-		-	-	0.25	1.5
	m	1/10m	1/20m	1/10m			-	-	-	-	-	-	0.05 π	Массой водила пренебречь
	m	1/4m	1/5m	1/10m		-		-		-	0.10	-	0.16 π	Шатун 3 рассматривать как тонкий однородный стержень

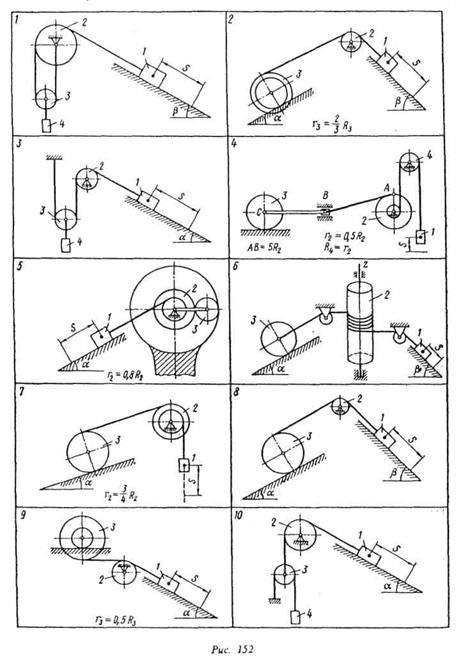
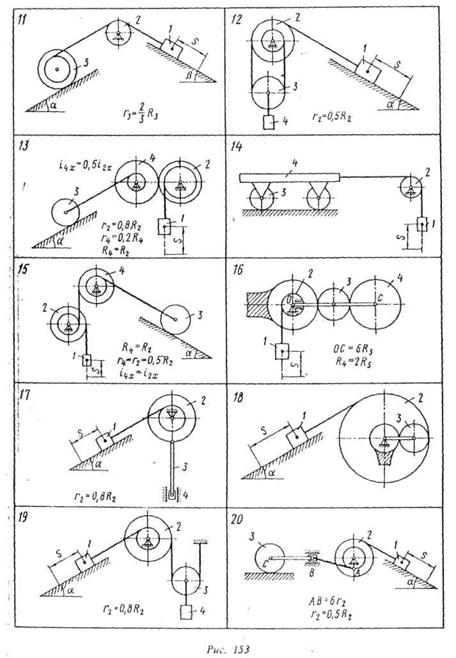
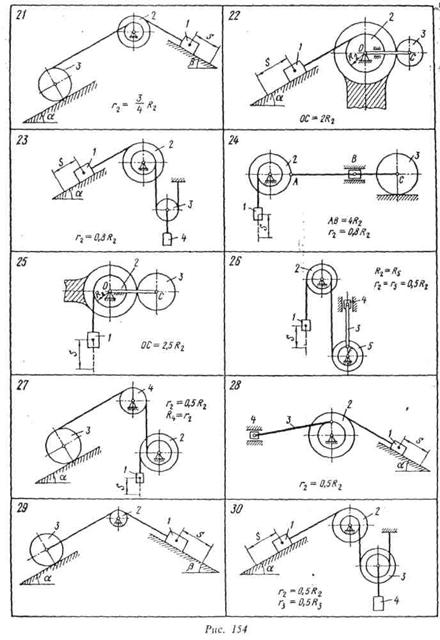
и катки для которых радиусы инерции не указаны, считать сплошными однородными цилиндрами.

Наклонные участки нитей параллельны соответствующим наклонным плоскостям

Пример выполнениязадания. Дано: т₁ — масса груза 1, т₂=2т₁, т₃ = т_1, т₄ = 0,5m₁, т₅ = 20т₁ R₂ = R₃ = 12 см, r₂ = 0,5R₂, r_з = 0,75R₃. R₅ = 20 см, AВ = l= 4R₃, i_2ξ = 8 см; i_3x= 10 см, α= 30°, f = 0.1, δ = 0,2 см, s = 0,06л м. Сопротивление качению "тела 2 не учитывать. Шатун 4 счи­тать тонким однородным стержнем; каток 5 — однородный сплошной цилиндр. Массами звена ВС₅ и ползуна В пренебречь. На рис. 155, апоказана механическая система в начальном положении.

Найти vi — скорость груза 1 в конечном положении.

Решение. Применим теорему об изменении кинетической энергии системы:

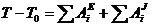(1)

где T_Q и T — кинетическая энергия системы в начальном и конечном положениях; 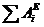— сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное; 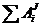— сумма работ внутренних сил системы на том же перемещении.

Для рассматриваемых систем, состоящих из абсолютно твердых тел,

соединенных нерастяжимыми нитями и стержнями,

Так как в началь­ном положении систе­ма находится в покое, то Т₀ = 0.

Следовательно, уравнение (1) принима­ет вид

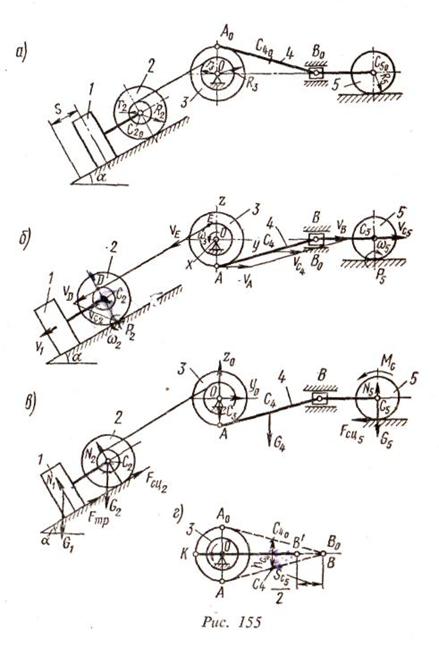
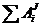=0 (2)

Для определения кинетической энергии T и суммы работ внешних сил надо изобразить систему в конечном положении (рис. 155, б, в)

Напишем кинематические соотношения между скоростями и перемещениями точек системы, т. е. уравне­ния связей, при этом скорости и перемеще­ния выразим соответ­ственно через скорости и перемещения гру­за 1.

Скорость центра масс С катка 2 равна скорости груза 1:

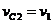(3)

Угловая скорость катка 2, мгновенный центр скоростей которого нахо­дится в точке Р₂,

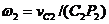
Учитывая (3), получим

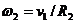(4)

Скорость точки D катка 2

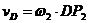
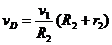т. е.

Скорость точки Е блока 3 равна скорости точки D катка 2:

v_E = v_D. (5)

Но

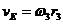
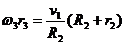Следовательно, по (5),

Так как

R₂ = 2r₂,

То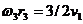

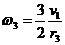откуда

(6)

Заменяя в формуле (6)

,

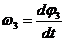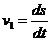
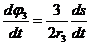получим

или

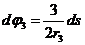
После интегрирования(при нулевых начальных условиях)

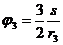⁽⁷⁾

Когда груз 1 пройдет путь s = 0,06л м, блок 3 повернется на угол φ₃

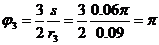
При этом повороте блока 3 на 180° его точка А₀ перейдет в конечное положение А и шатун 4 из начального положения А₀В₀ перейдет в ко­нечное положение АВ.

Каток 5 переместится влево при повороте блока 3 на угол π/2 и вправо при повороте блока еще на π/2; значит, конечное положение катка 5 совпадает с его начальным положением.

Таким образом, конечное положение всей системы вполне определено (рис. 155, б).

Вычислим кинетическую энергию системы в конечном положении как сумму кинетических энергий тел 1, 2, 3, 4, 5:

T=T₁ + T₂ + T₃ + T₄+T₅. (8)

Кинетическая энергия груза 1, движущегося поступательно,

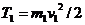. (9)

Кинетическая энергия катка 2, совершающего плоское движение,

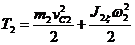(10)

где J_2ξ — момент инерции катка 2 относительно его продольной централь­ной оси С_2ξ

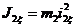(11)

Подставляя (3), (4), (11) в формулу (10), получаем

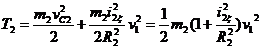
Кинетическая энергия тела 3, вращающегося вокруг оси Ох,

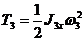(13)

где J_3x — момент инерции блока 3 относительно оси Ох:

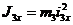(14)

Подставляя (6), (14) в формулу (13), получаем

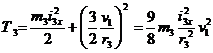
Кинетическая энергия шатуна 4, совершающего плоское движение,

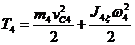
где v_C4 — скорость центра масс С₄ шатуна 4; ω₄ — угловая скорость ша­туна 4; J_4ξ — момент инерции шатуна относительно центральной оси С_4ξ. Для определения v_C4 и ω₄ найдем положение мгновенного центра ско­ростей шатуна 4. Так как скорости точек А и В в этот момент парал­лельны, то мгновенный центр скоростей шатуна 4 находится в бесконеч­ности; следовательно, угловая скорость шатуна в данный момент ω₄ = 0, а скорости всех его точек параллельны и равны между собой. Таким образом, кинетическая энергия шатуна 4

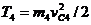(16)

где

v_C4 = v_A. (17)

Вращательная скорость точки А тела 3

v_A = ω₃R₃, (18)

или с учетом (14)

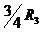
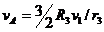
Поскольку г₃₌ получим

v_A = 2 v ₁

По (17)

v_C4 = v_A. V_C4 = 2v₁ (19)

После подстановки (19) в (16) выражение кинетической энергии ша­туна 4 принимает вид

Т₄=¹/2m₄(2v₁)²=2mv₁² (20)

Кинетическая энергия катка 5, совершающего плоское движение,

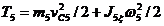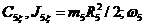
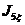где v_C5 — скорость центра масс С₅ катка 5; - момент инерции катка 5 (однородного сплошного цилиндра) относительно его центральной про­дольной оси — угловая скорость катка 5.

Так как каток катится без скольжения, то мгновенный центр скоростей находится в точке Р₅. Поэтому

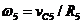Следовательно,

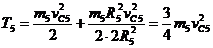
Так как звено ВС₅ совершает поступательное движение, то v_c5 = v_B но v_B = v_c4 =2 v₁. Значит, v_c5 = 2 v₁.

Поэтому выражение кинетической энергии катка 5 принимает вид

T_s = ³/4m₅ (2v₁)² = 3m₅ v₁² (21)

Кинетическая энергия всей механической системы определяется по формуле (8) с учетом (9), (12), (15), (20), (21):

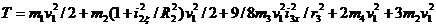
Подставляя сюда заданные значения масс, получаем

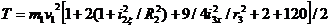
или

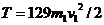(22)

Найдем сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении. Покажем внешние силы, приложенные к сис­теме (рис. 155, в).

Работа силы тяжести G_t

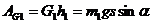(23)

Работа силы трения скольжения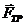

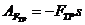
Так как

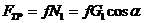
то

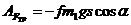(24)

Работа силы тяжести G₂

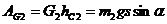(25)

Работа сил сцепления F_сц2, F_си5 катков 2 и 5 равна нулю, так как эти силы приложены в мгновенных центрах скоростей этих катков. Работа силы тяжести G₄

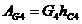
где h_C4 — вертикальное перемещение центра тяжести С₄ шатуна 4 из на­чального положения в его конечное положение (рис. 155, г):

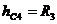
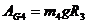. (26)

Работа пары сил сопротивления качению катка 5

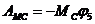(27)

где Мс = δN₅ =δG₅ ^— момент пары сил сопротивления качению катка 5; φ₅ — угол поворота катка 5.

Так как каток 5 катится без скольжения, то угол его поворота

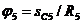(28)

где s_C5 — перемещение центра тяжести С₅ катка 5.

В данном примере работу пары сил сопротивления вычислим как сумму работ этой пары при качении катка 5 влево при повороте тела 3 на угол π/2 и качении вправо, когда тело 3 повернется еще на угол π/2.

Перемещение центра тяжести С₅ катка 5 равно перемещению ползуна В влево и право:

s_C5 = 2 (B₀B^/). (29)

Определим перемещение В₀В' при повороте тела 3 на угол π/2. За начало отсчета координаты точки В выберем неподвижную точку К плоскости (рис. 155, г). При этом повороте тела 3 шатун из положения А₀В₀ перейдет в положение KB'. Тогда

В₀В' = КВ₀ - KB¹,

где

КВ₀ = КО + ОВ₀ = R₃ +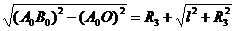

KB' = / = 4R₃.

Следовательно,

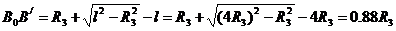. (30)

Подставляя (30) в (29), а затем в (28), находим полный угол поворота катка 5:

φ₅ = 1,76R₃/R₅. (31)

Работа пары сил сопротивления качению по (27)

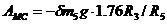(32)

Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (23) —(26) и (32):

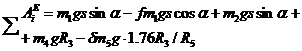Подставляя заданные значения масс, получаем

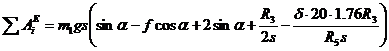
или

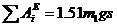(33)

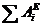Согласно теореме (2), приравняем значения Т и определяемые по формулам (22) и (33):

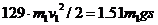откуда

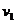= 0,21 м/с.

Задание Д.11. Исследование поступательного и вращательного движений твердого тела

Механическая система состоит из механизма (колес 1 и 2) и груза 3. К колесу 1 приложена пара сил с моментом М = М (t) (движущий момент) или движущая сила Р — Р (t).

Время t отсчитывается от некоторого момента (t = 0), когда угловая скорость колеса 7 равна ω₁₀. Момент сил сопротивления ведомого колеса 2 равен М_с. Другие силы сопротивления движению системы не учитывать.

Массы колес 1 и 2 равны т₁ и т₂, а масса груза 3 — m₃.

Радиусы больших и малых окружностей колес R₁ r₁ R₂, r₂.

Схемы механических систем показаны на рис. 156—158, а необходи­мые для решения данные приведены в табл. 48.

Найти уравнение движения тела системы, указанного в последней графе табл. 48.

Определить также натяжение нитей в заданный момент времени, а в вариантах, где имеется соприкасание колес 1 и 2, найти, кроме того, окружное усилие в точке их касания. Колеса 1 и 2, для которых радиусы инерции i_X1 и i_Х2 в табл. 48 не заданы, считать сплошными однородными дисками.

Пример выполнения задания. Дано: т₁ = 100 кг; т₂ = 150 кг; т₃ = 400 кг; М = 4200 + 200t Н • м; М_с = 2000 Н • м = const; R₁ = 60; R₂ = 40 см; r₂ = = 20 см; i_X1 = 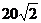i_x2 = 30 см; ω₁₀ = 2 рад/с.

Найти уравнение ср₂ = f(t) вращательного движения колеса 2 механизма, а также окружное усилие S в точке касания колес 1 и 2 и натяжение нити Г в момент времени t₁ = 1 (рис. 159, а).

Решение. В данной механической системе колеса 1и 2 механизма вращаются вокруг неподвижных осей, а поднимаемый груз 3 совершает поступательное движение.

Напишем дифференциальные уравнения движения каждого из этих трех тел, для чего отделим одно от другого, разрезав нить, удерживающую груз 3, и разъединив колеса 1и 2 в точках соприкасания зубцов (рис. 159,6).

К колесу 1механизма приложены сила тяжести 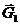движущий момент М, составляющие реакции подшипника 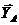, 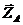окружное усилие 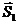и нормальная реакция 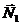колеса 2.

К колесу 2 механизма приложены сила тяжести, 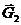момент сил сопро­тивления М_с, составляющие реакции подшипника 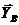, 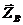натяжения Т нити, ккоторой подвешен груз 3, окружное усилие