Расчет сложных рам методом сил: использование симметрии, группировка неизвестных, симметричные и обратносимметричные нагрузки.
Теперь рассмотрим примеры, иллюстрирующие различные способы использования симметрии.
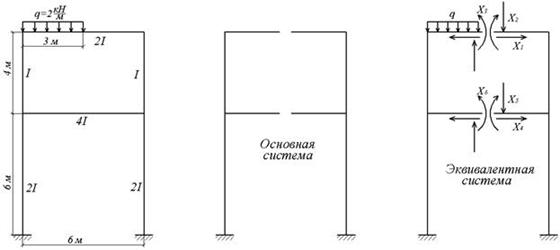
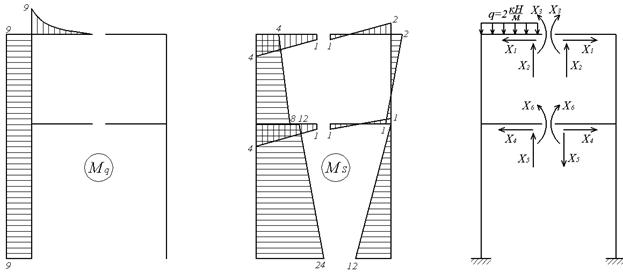
Пример 6.4. Построить эпюры Nz, Qy и Mx для симметричной рамы, загруженной несимметричной внешней нагрузкой (рис.6.11,а).
Заданная рама имеет два замкнутых бесшарнирных контура, следовательно, ее степень статической неопределимости 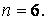
Записанная формально, без использования симметрии, система канонических уравнений метода сил имеет вид

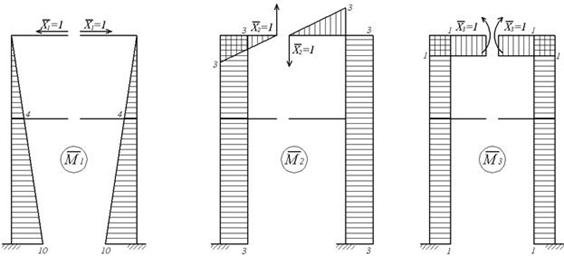
Из многих возможных вариантов выбора основной системы наиболее целесообразным, максимально упрощающим расчет, является вариант, представленный на рис.6.11,б, полученный путем разрезания каждого из ригелей посредине пролета. Так как разрез стержня приводит к появлению трех неизвестных факторов (двух сил и момента), то эквивалентная система (рис.6.11,в) будет состоять из двух жестко защемленных рам, одна из которых загружена только неизвестными реакциями, а другая — такими же неизвестными реакциями и внешней нагрузкой.
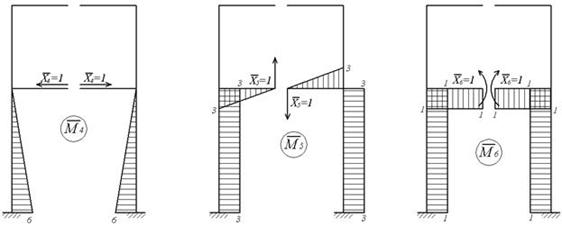
Указанный выбор основной системы позволяет не только получить простые единичные эпюры (рис.6.11,г-и), но, что особенно важно, при этом целый ряд побочных коэффициентов системы канонических уравнений обращается в ноль. Это те коэффициенты, которые получаются путем перемножения симметричной и кососимметричной эпюр:
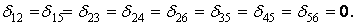
В силу теоремы о взаимности перемещений число нулевых коэффициентов удваивается. В результате формально записанная система канонических уравнений распадается на две самостоятельных системы:
| I) |  |
| II) | 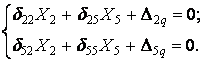 |
Вычисление коэффициентов этих систем уравнений (с обязательным учетом соотношения жестокостей элементов) приводит к следующим результатам:
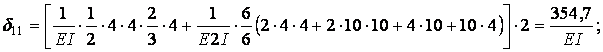
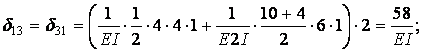
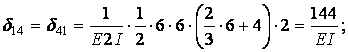
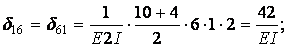
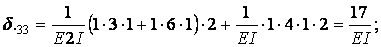
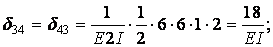
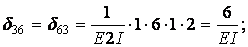
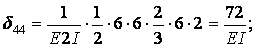
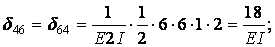
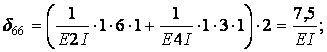
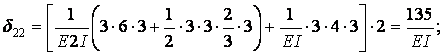
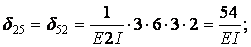
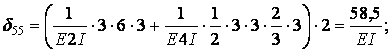
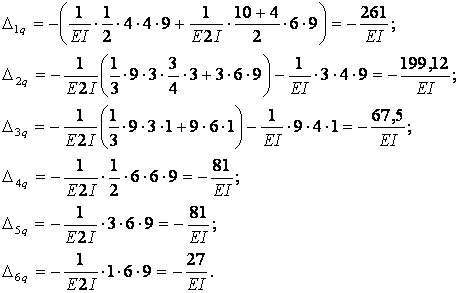
 | ||
| а | б | в |
 | ||
| г | д | е |
 | ||
| ж | з | и |
Рис.6.11. Использование симметрии (к примеру 6.4)
Для выполнения проверки вычисленных перемещений строим суммарную единичную эпюру 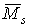 от одновременного действия шести единичных факторов (рис.6.12,б).
от одновременного действия шести единичных факторов (рис.6.12,б).
Вычисляем коэффициенты 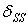 и
и 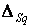 :
:
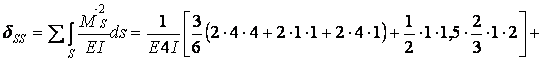
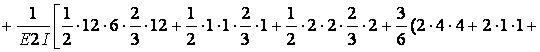
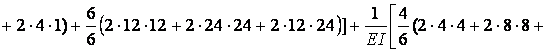
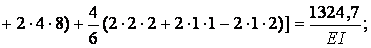
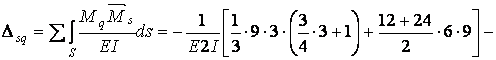
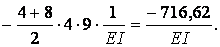
Выполняем проверку:
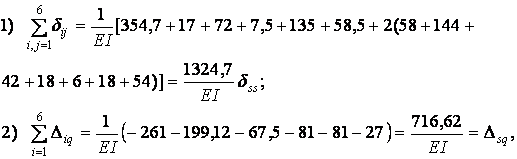
следовательно, коэффициенты и свободные члены систем канонических уравнений вычислены правильно.
 | ||
| а | б | в |
 | ||
| г | д | е |
Рис.6.12. Окончательные эпюры (к примеру 6.4)
Подставляя вычисленные значения перемещений, получим системы канонических уравнений I и II в виде:
| I. | 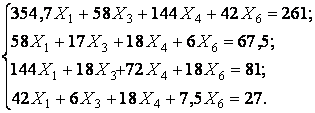 |
| II. | 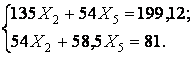 |
Решение систем I и II дает значения реакций лишних связей:
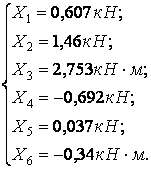
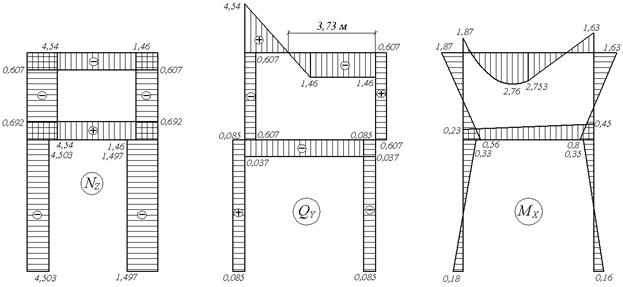
Окончательные эпюры Nz, Qy, Mx, построенные от одновременного действия вычисленных реакций и внешней нагрузки q (рис.6.12,в) показаны на рис.6.12,г,д,е.
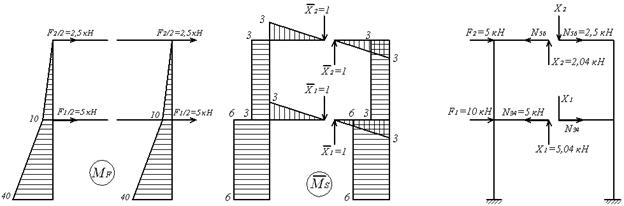
Пример 6.5. Построить эпюры Nz, Qy, Mx в симметричной раме (рис.6.13,а).
Рама имеет два замкнутых бесшарнирных контура, поэтому она шесть раз статически неопределима. При обычном подходе в этом случае было бы необходимо решить систему шести линейных уравнений, т.е. расчет был бы весьма трудоемким. Использование симметрии, как это будет показано ниже, позволит свести задачу к решению только лишь двух линейных уравнений.
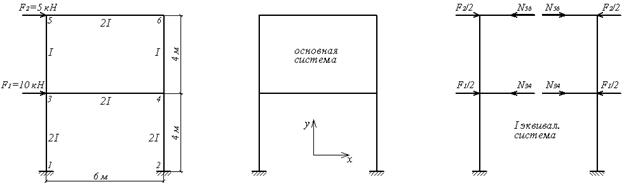
Выберем основную систему, разрезая каждый из ригелей посредине пролета (рис.6.13,б). Но, в отличие от предыдущего примера, сформируем две эквивалентных системы, одну из которых загрузим симметричными составляющими внешней нагрузки (рис.6.13,в), а другую — обратно симметричными составляющими (рис.6.13,г). Легко убедиться в том, что сумма внешних нагрузок, приложенных к обеим эквивалентным системам, равна внешней нагрузке, приложенной к заданной раме.
При действии симметричных самоуравновешенных сил 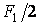 и
и 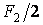 (рис.6.13,в), приложенных в узлах, в элементах рамы отсутствуют изгибающие моменты и поперечные силы, а продольные силы возникают только в ригелях и вычисляются непосредственно из условий равновесия узлов 3 и 5, или, что то же самое, 4 и 6:
(рис.6.13,в), приложенных в узлах, в элементах рамы отсутствуют изгибающие моменты и поперечные силы, а продольные силы возникают только в ригелях и вычисляются непосредственно из условий равновесия узлов 3 и 5, или, что то же самое, 4 и 6:
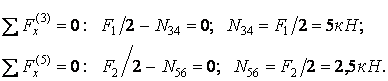
При действии обратносимметричных сил 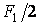 и
и 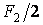 (рис.6.13,г) в разрезах, сделанных по оси симметрии рамы, возникают обратносимметричные неизвестные поперечные силы Х1, Х2, а продольные силы и изгибающие моменты обращаются в ноль как симметричные усилия при обратносимметричной нагрузке.
(рис.6.13,г) в разрезах, сделанных по оси симметрии рамы, возникают обратносимметричные неизвестные поперечные силы Х1, Х2, а продольные силы и изгибающие моменты обращаются в ноль как симметричные усилия при обратносимметричной нагрузке.
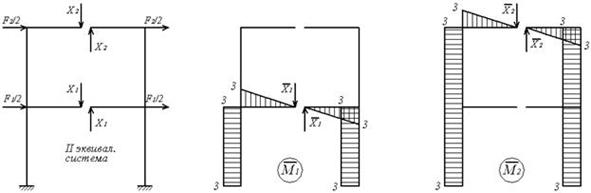
Таким образом, для расчета рамы нужно составить только два канонических уравнения метода сил:
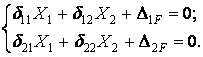
Единичные и грузовая эпюра изгибающих моментов показаны на рис.6.13,д,е,ж. Вычислим коэффициенты канонических уравнений путем перемножения соответствующих эпюр по правилу Верещагина:
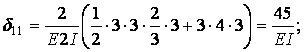
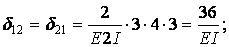
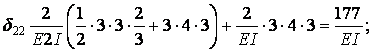
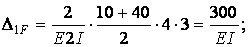
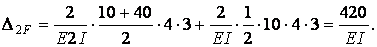
Единичные и грузовая эпюра изгибающих моментов показаны на рис.6.13,д,е,ж.
 | ||
| а | б | в |
 | ||
| г | д | е |
 | ||
| ж | з | и |
 | ||
| к | л | м |
Рис.6.13. К примеру 6.5
Для проверки вычисленных перемещений используем суммарную единичную эпюру изгибающих моментов 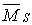 (рис.6.13,з).
(рис.6.13,з).
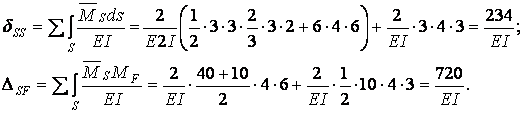
Проверка:
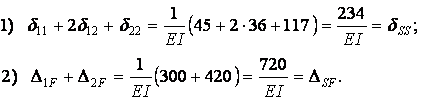
После подстановки найденных значений коэффициентов при неизвестных и свободных членов в канонические уравнения и умножения последних на EI получим
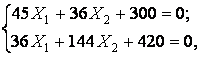
отсюда
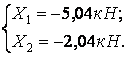
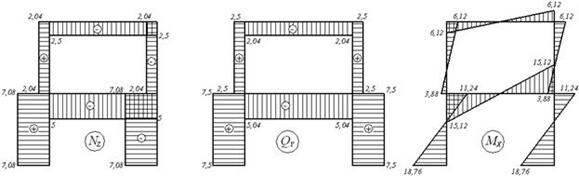
Таким образом, в результате раскрытия статической неопределимости исходная, шесть раз статически неопределимая система приведена к статически определимой системе (рис.6.13,и), загруженной внешней нагрузкой F1 и F2, продольными усилиями N34 и N56, а также вычисленными реакциями X1 и X2.
Эпюры продольных, поперечных сил и изгибающих моментов для заданной рамы показаны на рис.6.13,к,л,м.
Для выполнения универсальной кинематической проверки эпюры Мх используем суммарную единичную эпюру 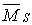 :
:
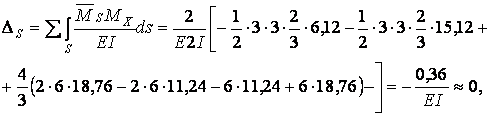
следовательно, задача решена правильно.
