Расчет арки на жестких опорах, имеющих заданную просадку.

Расчет арки на жестких опорах, имеющих заданную просадку.

Расчет безшарнирной арки

Бесшарнирная арка является трижды статически неопределимой системой. Для получения основной статически определимой системы надо у бесшарнирной арки удалить три связи. Для симметричных арок (рис. 9.5, а) основную систему принимают симметричной в виде двух криволинейных консолей (рис. 9.5, б). Для получения основной системы можно также включить в арку три шарнира (рис. 9.5, в). Удобнее применять первый способ. Вместо трех удаленных связей в разрезе прикладывают неизвестные усилия 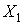, 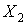и .

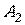Канонические уравнения будут иметь вид:

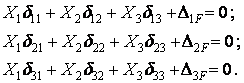
Так как силы 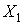и 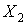симметричные, а сила 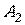— обратносимметричная, то 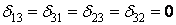. Система уравнений распадается на две независимые системы: в первую систему входят лишь симметрич­ные неизвестные 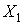и 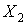; во вторую систему входит лишь одно уравне­ние, содержащее неизвестное :

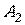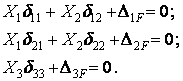
Перемещения находят по формулам Мора.

Для дальнейшего упрощения расчета в месте разреза можно доба­вить жесткие консоли, а неизвестные силы приложить по их концам (рис. 9.5, г).

а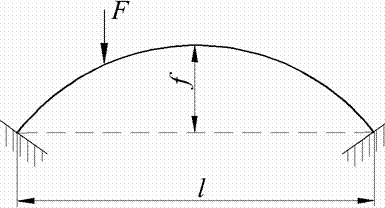
б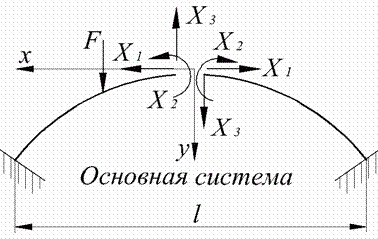
в
г

Рис. 9.5. Безшарнирная арка

Подберем длину консоли 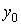, исходя из условия, чтобы побочное перемещение 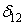обращалось в нуль, т.е.

.

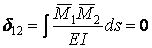Если ос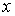и и 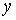направить так, как показано на рис. 9.5, б, то 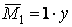; 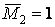, тогда положение точки 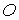(концы консоли) надо выбирать так, чтобы соблюдалось условие

.

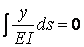Обозначим вертикальное расстояние от сечения до оси 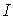через 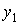, тогда

,

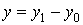где 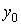— расстояние между осям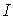и и , а условие

.

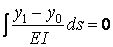Разобьем это условие на два интеграла:

.

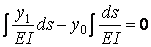откуда

.

(9.6)

Итак, если длина жестких консолей подобрана по (9.6), перемещение 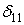обращается в нуль. Канонические уравнения этом случае при­нимают вид:

; ; .

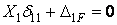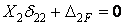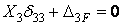Лишние неизвестные

; ; .

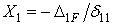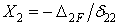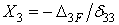Расчет статически неопределимых ферм методом сил: общий ход расчета при постоянной нагрузке.

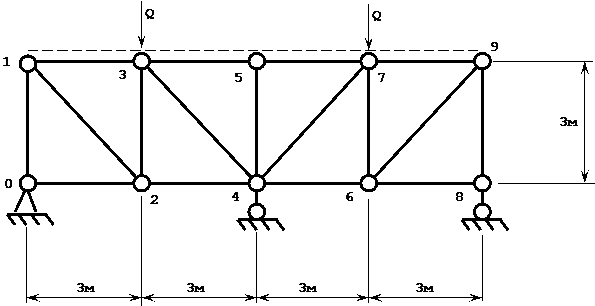
Схема 1

I. Выбор основной системы

Определим степень статической неопределимости:

N = R – 3 = 4 – 3 = 1

Система один раз статически неопределима.

δ₁₁ X₁ + δ_1p = 0

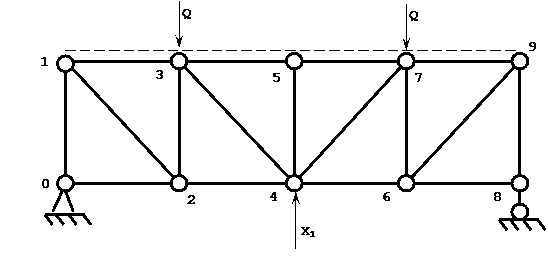
VI. Построение линий влияния для стержней средней панели

Сначала строим линии влияния в стержнях статически определимой фермы. Для стержней средней панели они приведены на схеме 3.

Далее строим линии влияния в исходной статически неопределимой ферме, исходя из условия:

N_i-j = N_i-j^ст.опр. + X₁*N_i-j , где

N_i-j– линия влияния в исходной статически неопределимой ферме,

N_i-j^ст.опр. –линия влияния в статически определимой ферме,

X₁ –линия влияния неизвестного усилия Х₁,

N_i-j –значение усилия в стержне от действия единичной силы Х₁=1.

N_3-5 = N_3-5^cт.опр. + 1*Х₁

N_3-2= N_3-2^cт.опр. + 0,5*Х₁

N_3-4 = N_3-4^cт.опр. – 0,7*Х₁

N_2-4 = N_2-4^cт.опр. + 0,5*Х₁

N_4-5 = N_4-5^cт.опр. + 0*Х₁

Итак, линии влияния в исходной статически неопределимой ферме приведены на схеме 4.

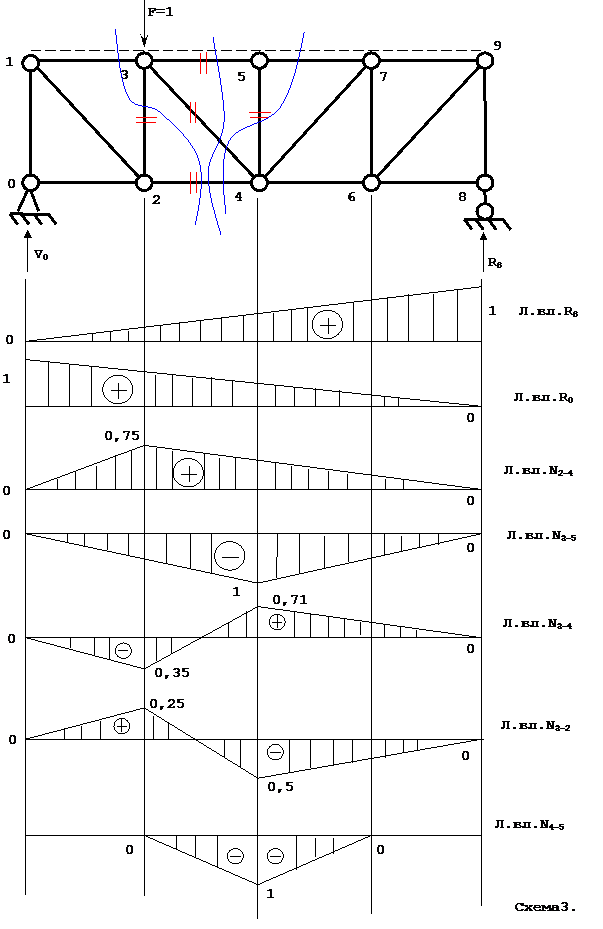
VII. Одну из линий влияния загрузим постоянной узловой нагрузкой и проверим

Для проверки правильности построения линий влияния загрузим заданной внешней нагрузкой линии влияния, например Х₁ и N_3-4, и проверим значение силы Х₁ и усилия в стержне 3-4.

Линия влияния Х₁:

Q*0,642 + Q*0,642 = 20*0,642 + 20*0,642 = 22 = X₁

Верно!

Линия влияния N_3-4:

Q*0,39 + Q*0,39 = 20*0,39 + 20*0,39 = 15,71 = N_3-4

Верно!

Проверки метода перемещений

Так же как и в методе сил, в методе перемещений можно выполнять статическую и кинематическую проверки. Но поскольку основная система метода перемещений кинематически определима, то кинематическая проверка является вспомогательной и выполняется всегда при правильных эпюрах изгибающих моментов в основной системе и при выполненной статической проверке.

Основной проверкой в методе перемещений является проверка равновесия узлов и других частей рамы. Количество проверяемых условий равновесия должно быть не меньше числа неизвестных метода перемещений.

Проверка правильности вычисления коэффициентов при неизвестных системы канонических уравнений метода перемещений выполняется аналогично проверке коэффициентов уравнений при расчете статически неопределимых систем методом сил. Для этого строится суммарная единичная эпюра моментов .

Умножая эту эпюру последовательно на каждую из единичных эпюр, получим сумму коэффициентов при неизвестных в соответствующем уравнении; так, умножая эпюру на эпюру , получим:

Аналогично, и т.д.

Сумма коэффициентов при неизвестных i-го уравнения должна равняться значению r_is, где

(7.12)

Таким образом, проверка вычисленных значений коэффициентов, входящих в первое каноническое уравнение метода перемещений, состоит в проверке условия

(7.13)

Аналогично проверяются и коэффициенты всех остальных уравнений. Как и в методе сил, такая проверка называется построчной.

Чаще используется универсальная проверка, которая состоит в том, что результат умножения эпюры на саму себя должен равняться сумме всех коэффициентов при неизвестных системы канонических уравнений. Действительно,

(7.14)

Для проверки свободных членов канонических уравнений необходимо суммарную единичную эпюру моментов умножить на эпюру , построенную от внешней нагрузки в статически определимой системе, полученной из заданной системы или основной системы метода перемещений устранением лишних связей, в том числе обязательно тех связей, реакции в которых определяются:

(7.15)

Результат перемножения (7.15) должен равняться сумме всех свободных членов канонических уравнений:

(7.16)

Достаточной проверкой правильности окончательной эпюры моментов являются, как уже отмечалось, статические проверки, суть которых будет подробно рассмотрена ниже на конкретных примерах.

Можно также выполнить дополнительную кинематическую проверку подобно тому, как это делается в методе сил. Для этого необходимо построить единичные эпюры в основной системе метода сил и перемножить их или суммарную единичную эпюру с окончательной эпюрой изгибающих моментов. При правильном расчете результат такого перемножения должен быть равен нулю. Эта проверка служит контролем правильности принятых для расчета единичных эпюр и грузовой эпюры изгибающих моментов.

Рис. 24

Неизвестными являются изгибающие моменты, возникающие в сечении неразрезной балки над опорами.

Выделим из основной системы четыре примыкающих друг к другу пролета со средней опорой номером n и построим единичные и грузовые эпюры (рис. 25). Из анализа единичных эпюр видно, что в любом каноническом уравнении только три единичных коэф­фициента будут отличны от нуля. Напишем одно из канонических уравнений в общем виде:

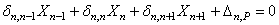. (14.22)

Подсчитаем единичные и грузовые коэффициенты, применяя правило Верещагина «перемножения» эпюр:

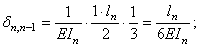
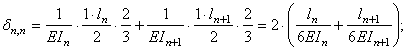
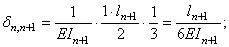
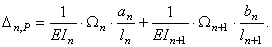(14.23)

Подставим найденные коэффициенты в (14.22), получим:

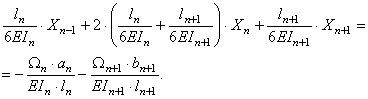(14.24)

В случае балки постоянного сечения J₁ = J₂ =...= J_n = J_n+1 и введя обозначения X_n-1 = M _n-1; X_n = M_n; X_n+1 = M_n+1, получим:

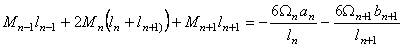. (14.25)

Это и есть уравнение трех моментов для неразрезной балки постоянного сечения. В этом урав­нении неизвестными являются из­гибающие моменты на опорах. Если у неразрезной балки все опоры шар­нирные, то таких уравнений можно составить столько, сколько у балки промежуточных опор.

При наличии на концах балки нагруженных консолей, изгибающие моменты на крайних опорах войдут в уравнение трех моментов, как из­вестные величины, а при отсутствии консолей эти моменты будут равны 0.

Если конец неразрезной балки защемлен, то для применения уравнения (14.25) необходимо, отбросив заделку, ввести с ее сто­роны дополнительный пролет 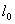=0 (рис.25). Такая системабудет деформироваться также, как балка с жесткой заделкой.

Рис. 25

Решая совместно, составленные таким образом уравнения, най­дем все неизвестные изгибающие моменты на опорах. Далее для построения эпюр M и Q, каждый пролет неразрезной балки рас­сматриваем как балку на двух шарнирных опорах, загруженных внешней нагрузкой и двумя опорными моментами. Ординаты эпюр могут быть подсчитаны по формулам:

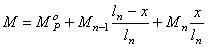, (14.26)

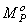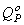где и - ординаты эпюр М и Q от внешней нагрузки в основной системе.

Чтобы убедиться в правильности построения эпюр М и Q необ­ходимо провести проверку равновесия неразрезной балки по уравнениям: ; .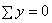

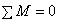Для этого следует определить вертикальные опорные реакции неразрезной балки, используя эпюру Q:

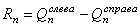. (14.27)

Рис.1

Например, балка на рис. 1, а является один раз статически неопределимой, так как имеет 4 связи и 4 неизвестные опорные реакции, а количество независимых уравнений равновесия – 3. В раме, показанной на рис. 3, а, число наложенных связей и опорных реакций в них равно 5, и эта рама является дважды статически неопределимой. Если в один из стержней балки (рамы) врезан шарнир, то количество связей уменьшается на единицу, так как становится возможным взаимный поворот сечений, примыкающих к шарниру. Появляется дополнительное уравнение для определения опорных реакций: "изгибающий момент в шарнире равен нулю" или можно сказать по-другому: "сумма моментов всех сил, расположенных слева (или справа) от шарнира, равна нулю". Так, балка с врезанным в точке Е шарниром, показанная на рис. 2, а, является один раз статически неопределимой: от 5 опорных связей надо вычесть одну связь, связанную с наличием дополнительного шарнира в точке Е. Из четырех оставшихся связей одна является лишней. Можно сосчитать степень статической неопределимости этой балки и иначе: для определения пяти опорных реакций можно составить четыре уравнения статики (дополнительное уравнение "изгибающий момент в шарнире Е равен нулю"). Разность между числом реакций и количеством уравнений статики равна единице, то есть балка один раз статически неопределима.

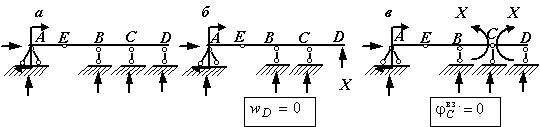
Рис.2

Рис.3

Следует различать внешне статически неопределимые и внутренне статически неопределимые системы.

Внешне статически неопределимой называют такую систему, которая имеет только лишние внешние связи, т.е. лишние опорные за­крепления. Примером внешне статически неопределимой плоской системы являетсятрехпролетная рама (рис. 4).

Рис.4

Степень статической неопределимости внешне статически неопределимой системы S легко установить путем вычитания из общего числа опорных стержней m количество независимых урав­нений равновесия n, которое может быть составлено для данной системы (одно - для одномерных; три - для плоских и шесть - для пространственных систем).

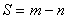. (14.1)

Для плоской рамы, изображенной на рис.4, учитывая, что защемление эквивалентно трем опорным стержням, получаем:

m = 3 + 2×2 +1 = 8; S = m - n = 8-3 = 5,

т.е. данная система 5 раз статически неопределима.

Внутренне статически неопределимой называют сис­тему, обладающую лишними связями, введенными для взаимного соединения частей системы.

Двухопорная рама с затяжкой (рис. 5, а) внутренне один раз статически неопределима. Статически определимая система (рис. 5, б) получена из заданной (рис. 5, а) путем разрезания за­тяжки ab. И при этом взаимодействие частей затяжки заменяется только одной неизвестной осевой силой N₁. Следовательно, в ста­тически определимой системе, изображенной на рис. 5, б имеем одно лишнее неизвестное N₁ , которое невозможно определить при помощи метода сечений. Поэтому заданная система (рис. 5, а) яв­ляется один раз статически неопределимой.

Если затяжку жестко заделать в стойки, как это показано на рис. 6, а, то получим трижды статически неопределимую систему.

Действительно, в данном случае после разрезания нижнего ригеля ab, взаимодействие частей ac и bc характеризуется уже тремя неизвестными усилиями N₁, Q₁, M₁(рис.6, б), которые нельзя определить из условия равновесия. Поэтому система, изображенная на рис. 6, a является три раза внутренне статически неопредели­мой.

Рис.5 Рис.6

Отсюда можно сделать вывод, что в плоских системах, замк­нутый бесшарнирный контур имеет три лишние связи. Следова­тельно, если плоская система содержит n замкнутых контуров, то она, очевидно, будет 3n раз статически неопределима.

На рис. 7 показана плоская рама, имеющая в первом (а) случае три внешние связи, а во втором случае (б) - пять. Значит, в первом случае рама имеет необходимое для статической определи­мости количество внешних связей, а во втором же - две дополни­тельные внешние связи. Однако в обеих ситуациях рама статически неопределима, т.к. конфигурация ее такова, что не позволяет опре­делить усилия во всех ее элементах, используя только уравнения равновесия. Следовательно, для окончательного ответа на вопрос о статической определимости системы необходимо проведение сов­местного анализа наложенных на систему внешних и внутренних связей.

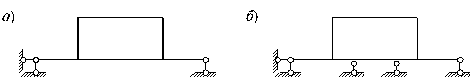
Рис. 7

Рассмотрим другие рамы, которые содержат замкнутые контуры (рис.8).

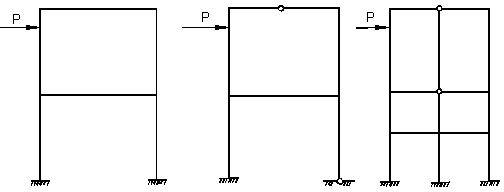
а) б) в)

Рис.8

Первая рама (рис.8,а) имеет шесть простых внешних связей при трёх необходимых для плоской системы. Следовательно, система имеет Л = 6 – 3 = 3 лишние внешние связи. Система имеет один замкнутый контур К= 1, который имеет три лишние внутренние простые связи, т.е. трижды статически неопределим. Следовательно, степень статической неопределимости системы 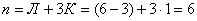. Вторая рама (рис.8, б) имеет пять внешних простых связей при трёх необходимых. Следовательно, Л=5–3=2 и система внешним образом дважды статически неопределима. Система имеет два замкнутых контура К=2, каждый из которых трижды статически неопределим, следовательно, внутренним образом система 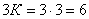шесть раз была бы статически неопределима, если бы не было внутреннего шарнира. Последний соединяет три стержня (m = 3) и поэтому даёт системе (m – 1) = 3–1=2 степени свободы. Таким образом, степень свободы статической неопределимости второй рамы можно вычислить по общей формуле:

,

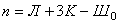где Ш₀ – число простых врезанных шарниров, К – число замкнутых контуров, Л – число лишних внешних связей.

В результате получаем: .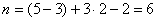

Третья рама (рис.8, в) имеет Л = 9 – 3 = 6, К = 4, Ш₀ = 2 + 3 = 5, следовательно, .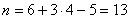

Отметим, что степень статической неопределимости стержневой системы и её степень свободы связаны равенством .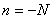

Рассмотрим еще несколько примеров определения степени статической неопределимости стержневых и рамных систем. На рис. 9 показано несколько рам. Последовательно рассмотрим их.

а) Рама имеет четыре дополнительные внешние связи и три взаимные связи, т. е. семь раз статически неопределима.

б) Полагаем сначала, что шарнир А отсутствует. Тогда имеются две внешние и три внутренние дополнительные связи. Система без шарнира А была бы пять раз статически неопределимой.

Шарнир А принадлежит одновременно трем стержням. Его можно рассматривать как два совпавших шарнира. Так как каждый шарнир снимает одну связь, т. е. разрешает поворот одного сечения относительно другого, то можно сказать, что шарнир А снимает две связи. Система становится, таким образом, вместо пяти — три раза статически неопределимой.

Обобщая сказанное, можно сделать вывод, что шарнир снимает число связей, на единицу меньшее числа сходящихся в нем стержней. В данном случае в шарнире А сходятся три стержня и шарнир снимает две связи.

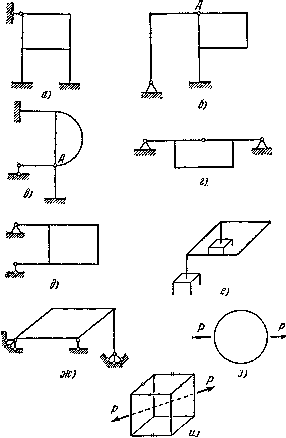
Рис.9. Примеры рамных статически неопределимых конструкций:

а) статически неопределимая — семь, б) — три, в) — четыре, г) — три,

е) — двенадцать, ж) — семь, и) — тридцать раз статически неопределима

в) Если бы шарнир А отсутствовал, система была бы четыре раза внешним образом и три раза внутренним образом статически неопределимой, т.е. всего семь раз. Шарнир А снимает число связей, на единицу меньшее числа сходящихся в нем стержней, т. е. три связи. Рама четыре раза статически неопределима.

г) Рама три раза статически неопределима.

д) Внешние связи не удовлетворяют условиям кинематической неизменяемости. Это — механизм, точнее говоря, мгновенный механизм. Система имеет возможность поворачиваться относительно верхней опоры как жесткое целое Понятно, что угол поворота будет небольшим. Нижняя связь заклинится и будет достигнуто какое-то положение равновесия, но новое положение связей будет зависеть от жесткости системы. К раме неприменимы основные принципы сопротивления материалов: принцип неизменности начальных размеров и принцип независимости действия сил.

е) Рама — пространственная. Имеется шесть дополнительных внешних связей (лишняя заделка) и шесть дополнительных взаимных связей (замкнутый контур). Система 12 раз статически неопределима.

ж) Система семь раз статически неопределима (один раз внешним образом и шесть раз — внутренним).

з) Здесь для плоской рамы не показаны внешние связи, но дана система внешних сил, удовлетворяющая условиям равновесия. В таком случае условились считать, что дополнительных внешних связей нет, и положение рамы в пространстве считается определенным; рассматриваются только внутренние связи. Система три раза статически неопределима.

и) Здесь также рассматриваются только внутренние связи, поскольку система указанных внешних сил удовлетворяет условиям равновесия. Нужно подсчитать, сколько сечений необходимо сделать в раме, чтобы, с одной стороны, она не «рассыпалась», а с другой, чтобы в ней не осталось ни одного замкнутого контура. Таких сечений следует сделать пять (см. рис. 9, и). Система 30 раз статически неопределима.

Метод сил

Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил».

Выбор основной системы

Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной систе­мы. После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо ввести вместо связей неизвестные силовые факторы, которые принято называть лишними неизвестными. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы будем обозначать X_i, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы X_i, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.

Основную систему с приложенными к ней лишними неизвестными Х₁, Х₂ ,...X_n и внешней нагрузкой Р называют эквивалентной системой при условии, что её действительные перемещения согласуются с наложенными на исходную систему связями. Для каждой статически неопределимой заданной системы (рис. 10, а) можно подобрать, как правило, различные основные системы (рис. 10, б, в), однако их должно объединять следующее условие - основная система должна быть статически определимой и геометрически неизменяемой (т.е. не должна менять свою гео­метрию без деформаций элементов).

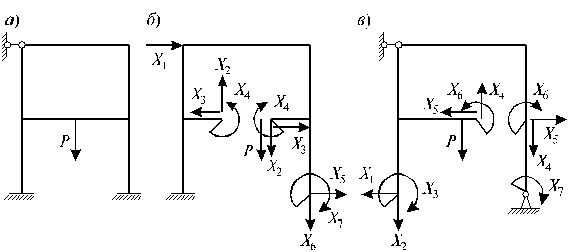
Рис. 10

Выбор основной системы (ОС) является непростым. Неудачный выбор ОС может привести к значительной трудоемкости решения, а иногда и к грубой ошибке. Нельзя руководствоваться только одним правилом образования основной системы, а именно, что число отбрасываемых связей должно быть равным степени статической неопределимости. Надо обязательно следить еще и за тем, какие связи отбрасываются. Некоторые связи отбрасывать недопустимо. При выборе основной системы надо следить кроме всего прочего и за геометрической неизменяемостью всей системы и отдельных ее частей.

Например, для рамы, показанной на рис. 11, можно предложить основные системы, а), б),..., которые получены путем отбрасывания семи дополнительных связей в различных комбинациях. Вместе с тем нужно помнить, что не всякая система с семью отброшенными связями может быть принята как основная. На рис. 12 показано три примера для той же рамы, в которой также отброшено семь связей, однако сделано это неправильно, так как оставшиеся связи не обеспечивают кинематической неизменяемости системы (рис.12, а, б), с одной стороны, и статической определимости во всех узлах,— с другой (рис.12, в).

Рис.11

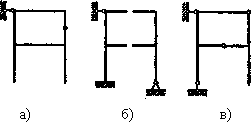
Рис.12

Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.

1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.13, б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.13, а).

2. Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n = 3 (рис.14, а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.14, б).

3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.14, в). В частных случаях (рис.14, г) рассечение стержня по шарниру освобождает две связи (рис.14, д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.14, е).

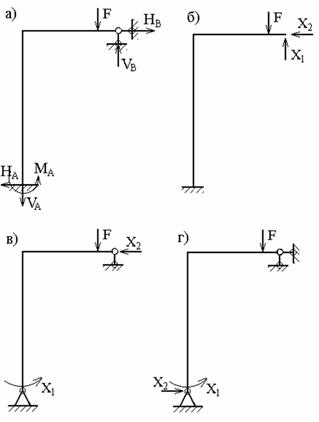
Рис. 13

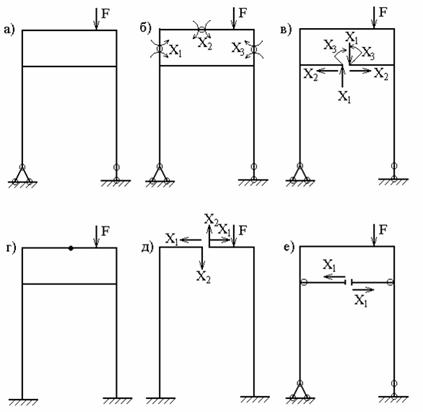
Рис. 14

Среди связей статически неопределимой системы различают абсолютно необходимые и условно необходимые. К абсолютно необходимым относятся связи, при удалении которых система становится геометрически изменяемой. Для абсолютно необходимой связи характерна статическая определимость усилия в ней, т.е. реакция такой связи может быть вычислена из условия равновесия. При выборе основной системы абсолютно необходимые связи отбрасывать нельзя.

Связи, при удалении которых система продолжает оставаться геометрически неизменяемой, называются условно необходимыми. Система, у которой удалили такую связь, может являться основной системой метода сил.

Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этой лекции. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.

Расчет арки на жестких опорах, имеющих заданную просадку.

Расчет безшарнирной арки

Бесшарнирная арка является трижды статически неопределимой системой. Для получения основной статически определимой системы надо у бесшарнирной арки удалить три связи. Для симметричных арок (рис. 9.5, а) основную систему принимают симметричной в виде двух криволинейных консолей (рис. 9.5, б). Для получения основной системы можно также включить в арку три шарнира (рис. 9.5, в). Удобнее применять первый способ. Вместо трех удаленных связей в разрезе прикладывают неизвестные усилия 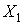, 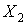и .

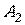Канонические уравнения будут иметь вид:

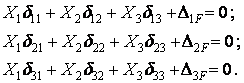
Так как силы 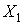и 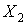симметричные, а сила 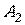— обратносимметричная, то 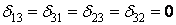. Система уравнений распадается на две независимые системы: в первую систему входят лишь симметрич­ные неизвестные 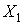и 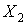; во вторую систему входит лишь одно уравне­ние, содержащее неизвестное :

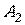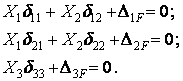
Перемещения находят по формулам Мора.

Для дальнейшего упрощения расчета в месте разреза можно доба­вить жесткие консоли, а неизвестные силы приложить по их концам (рис. 9.5, г).

а
б
в
г

Рис. 9.5. Безшарнирная арка

Подберем длину консоли 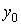, исходя из условия, чтобы побочное перемещение 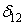обращалось в нуль, т.е.

.

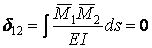Если ос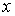и и 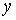направить так, как показано на рис. 9.5, б, то 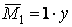; 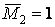, тогда положение точки 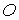(концы консоли) надо выбирать так, чтобы соблюдалось условие

.

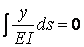Обозначим вертикальное расстояние от сечения до оси 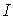через 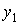, тогда

,

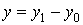где 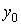— расстояние между осям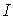и и 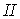, а условие

.

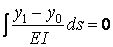Разобьем это условие на два интеграла:

.

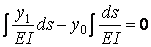откуда

.

(9.6)

Итак, если длина жестких консолей подобрана по (9.6), перемещение 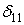обращается в нуль. Канонические уравнения этом случае при­нимают вид:

; ; .

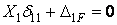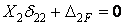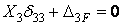Лишние неизвестные

; ; .
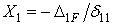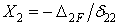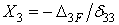