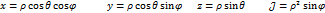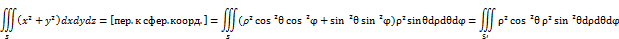Определение двойного интеграла

Пусть в некоторой области D на координатной плоскости XOY определена функция двух переменных z = f (x, y). Предполагается, что граница области D состоит из конечного числа кривых, заданных уравнениями вида y = f (x) или x = φ (y), где f (x) и φ (y) – непрерывные функции.

1. Разобьем область D на бесконечно малые ячейки прямыми, параллельными координатным осям.

2. В каждой ячейке выберем точку C_i,j(x_i, y_j).

3. Вычислим значения f (x_i, y_j) функции в этой точке.

4. Эти значения f (x_i, y_j) умножим на площади ячеек, из которых бралась точка: f (x_i, y_j)·Δ x_i·Δ y_j.

5. Все эти произведения сложим:

.

Полученная сумма называется двойной интегральной суммой.

Назовем диаметром d(D) области D наибольшее расстояние между точками этой области. Обозначим через λ наибольший из диаметров частичных областей D_i

.

О п р е д е л е н и е. Двойным интегралом называется предел двойной интегральной суммы при условии стремления к нулю диаметров всех ячеек, если он существует и не зависит от способа разбиения области D, от способа выбора точек C_i,j (x_i, y_j) внутри каждой ячейки

.

В этом случае функция f (x, y) называется подынтегральной, D — областью интегрирования, x и y — переменными интегрирования, ds (или dx·dy) – элементом площади.
Мы предполагаем, что функция f (x, y) ограничена. Как и для функции одной переменной, это условие является необходимым условием интегрируемости. Однако оно не является достаточным, т.е. существуют ограниченные, но не интегрируемые функции. Примером таких функций является функция, определенная на квадрате

{ (x, y) | 0 ≤ x ≤ 1; 0 ≤ y ≤ 1}

следующим образом:

Т 1. Функция f (x, y), непрерывная в замкнутой ограниченной области D, интегрируема в этой области.
Т2. Функция f (x, y),ограниченная в замкнутой ограниченной области D и непрерывная в ней всюду, кроме точек, лежащих на конечном числе кривых, являющихся графиками непрерывных функций вида y = ψ(x) или x = φ (y), интегрируема в этой области.

Вычисление площади плоской фигуры двойным интегралом

Если положить f (x, y) = 1 всюду в области D, то непосредственно из определения двойного интеграла получим выражение площади s области D в виде двойного интеграла:

Свойства двойных интегралов

1. Линейное свойство

.

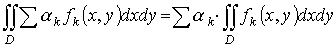2. Если функции f (x, y) и g(x, y) интегрируемы в области D, то их алгебраическая сумма также интегрируема в этой области и

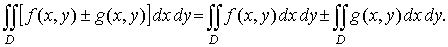
3. Аддитивное свойство по области интегрирования

.

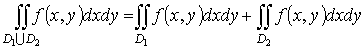4. Теорема о среднем. Если функция f (x, y) непрерывна в области D, то в этой области найдется такая точка ( ξ; μ), что

,

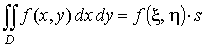где s — площадь фигуры D.

Билет8(тройные интегралы:опр, их св-ва и вычисления)

Билет9(замена переменных в кратных интегралах)

Замена переменных в кратных интегралах.

В математическом анализе кратным или многократным интегралом называют множество интегралов, взятых от переменных. Например:

Замечание: кратный интеграл − это определенный интеграл, при его вычислении всегда получается число.

В двойных интегралах.

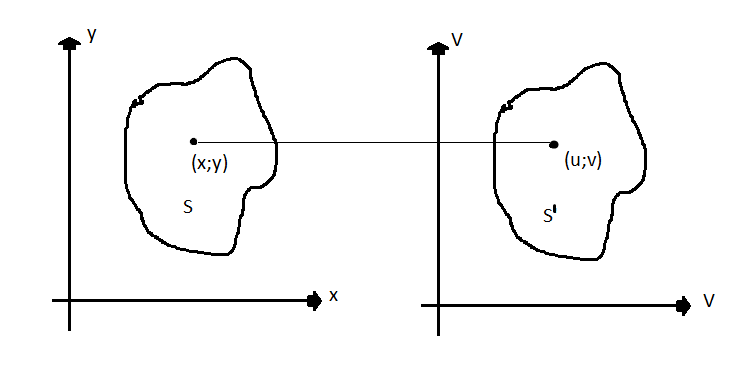
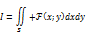
Ф-ии х; у однозначные и непрерывные на S.

Пусть 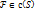x=x(u;v) y=y(u;v)

При замене «х» и «у» на «u» и «v» область S переходит в S’, тогда

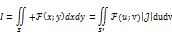
Где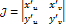

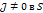
Для двойных интегралов часто используется переход от декартовых к полярным координатам

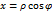
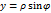тогда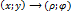

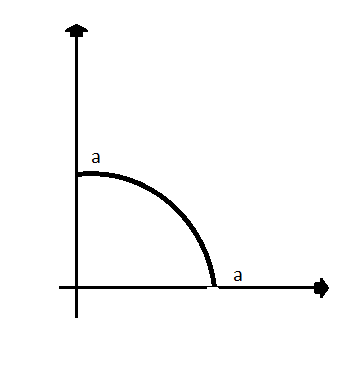
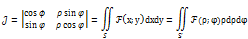Переход от декартовых координат к полярным целесообразен, если область интегрирования-часть круга.

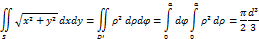
В тройных интегралах

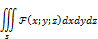
Пусть 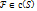x=x(u;v;w) y=y(u;v;w) z=z(u;v;w) -однозначны и непрерывны, вместе с ЧП на области S

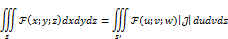
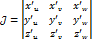
Наиболее распр. заменами в тройном интеграле являются:

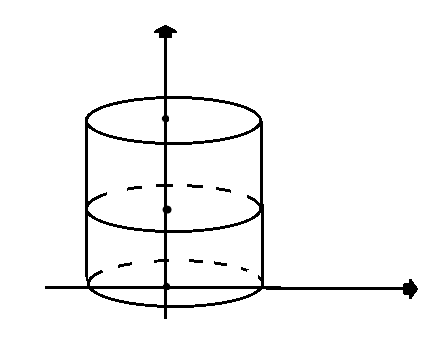
1) Переход к цилиндрическим координатам:

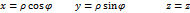
Переход к цилиндрическим координатам целесообразен, если область интегрирования-часть циллинра, или сечения плоскостями, параллельными одной из координатных плоскостей есть часть круга, или круг

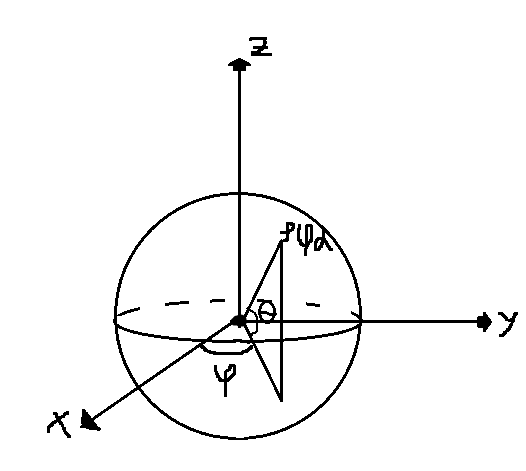
2) Переход к сферическим координатам