Вектор нормали прямой (нормальный вектор)

Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), причём все векторы нормали прямой будут коллинеарными (сонаправленными или нет – без разницы).

Разборки с ними будут даже проще, чем с направляющими векторами:

Если прямая задана общим уравнением 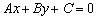в прямоугольной системе координат, то вектор 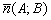является вектором нормали данной прямой.

Если координаты направляющего вектора 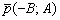приходиться аккуратно «вытаскивать» из уравнения, то координаты вектора нормали 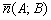достаточно просто «снять».

Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:

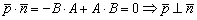
Приведу примеры с теми же уравнениями, что и для направляющего вектора:

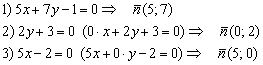
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Если известен вектор нормали, то однозначно определено и направление самой прямой – это «жёсткая конструкция» с углом в 90 градусов.

Как составить уравнение прямой по точке и вектору нормали?

Если известна некоторая точка 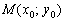, принадлежащая прямой, и вектор нормали 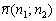этой прямой, то уравнение данной прямой выражается формулой:

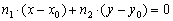
Пример 9

Составить уравнение прямой по точке 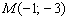и вектору нормали 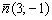. Найти направляющий вектор прямой.

Решение: Используем формулу:

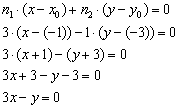
Общее уравнение прямой получено, выполним проверку:

1) «Снимаем» координаты вектора нормали с уравнения 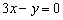: 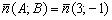– да, действительно, получен исходный вектор из условия (либо должен получиться коллинеарный исходному вектор).

2) Проверим, удовлетворяет ли точка 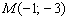уравнению :

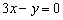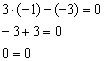
Верное равенство.

После того, как мы убедились в том, что уравнение составлено правильно, выполним вторую, более лёгкую часть задания. Вытаскиваем направляющий вектор прямой: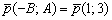

Ответ: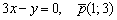

На чертеже ситуация выглядит следующим образом:

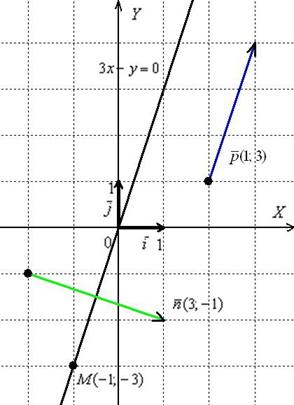
В целях тренировки аналогичная задача для самостоятельного решения:

Пример 10

Составить уравнение прямой по точке 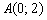и нормальному вектору 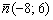. Найти направляющий вектор прямой.

Заключительный раздел урока будет посвящен менее распространённым, но тоже важным видам уравнений прямой на плоскости

Уравнение прямой в отрезках.
Уравнение прямой в параметрической форме

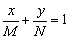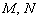Уравнение прямой в отрезках имеет вид , где – ненулевые константы. Некоторые типы уравнений нельзя представить в таком виде, например, прямую пропорциональность 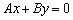(так как свободный член 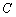равен нулю и единицу в правой части никак не получить).

Это, образно говоря, «технический» тип уравнения. Обыденная задача состоит в том, чтобы общее уравнение прямой 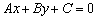представить в виде уравнения прямой в отрезках 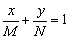. Чем оно удобно? Уравнение прямой в отрезках позволяет быстро найти точки пересечения прямой с координатными осями, что бывает очень важным в некоторых задачах высшей математики.

Найдём точку пересечения прямой с осью 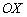. Обнуляем «игрек», и уравнение принимает вид 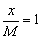. Нужная точка получается автоматически: .

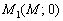Аналогично с осью 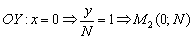– точка, в которой прямая пересекает ось ординат.

Действия, которые я только что подробно разъяснил, выполняются устно.

Пример 11

Дана прямая 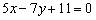. Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.

Решение: Приведём уравнение к виду 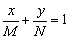. Сначала перенесём свободный член в правую часть:

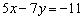
Чтобы получить справа единицу, разделим каждый член уравнения на –11:

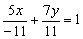
Делаем дроби трёхэтажными:

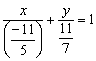
Точки пересечения прямой с координатными осями всплыли на поверхность:

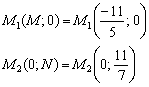
Ответ: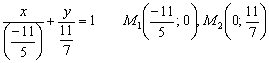

Осталось приложить линеечку и провести прямую.

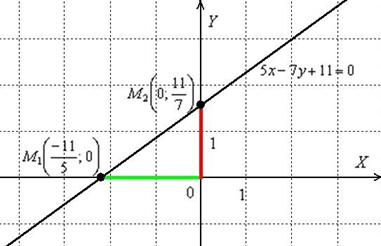
Легко усмотреть, что данная прямая однозначно определяется красным и зелёным отрезками, отсюда и название – «уравнение прямой в отрезках».

Конечно, точки 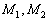не так трудно найти и из уравнения 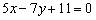, но задача всё равно полезная. Рассмотренный алгоритм потребуется для нахождения точек пересечения плоскости с координатными осями, для приведения уравнения линии второго порядка к каноническому виду и в некоторых других задачах. Поэтому пара прямых для самостоятельного решения:

Пример 12

Составить уравнение прямой в отрезках и определить точки её пересечения с координатными осями.

а)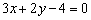

б)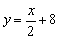

Решения и ответы в конце. Не забывайте, что при желании всё можно начертить.

Как составить параметрические уравнениЯ прямой?

Параметрические уравнения прямой больше актуальны для прямых в пространстве, но без них наш конспект осиротеет.

Если известна некоторая точка 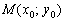, принадлежащая прямой, и направляющий вектор 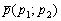этой прямой, то параметрические уравнения данной прямой задаются системой:

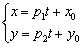
Пример 13

Составить параметрические уравнения прямой по точке 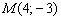и направляющему вектору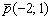

Решение закончилось, не успев начаться:

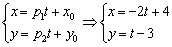
Параметр «тэ» может принимать любые значения от «минус бесконечности» до «плюс бесконечности», и каждому значению параметра соответствует конкретная точка плоскости. Например, если 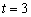, то получаем точку .

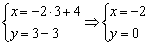Обратная задача: как проверить, будет ли точка 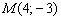условия принадлежать данной прямой?

Подставим координаты точки 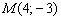в полученные параметрические уравнения:

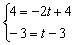
Из обоих уравнений следует, что 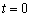, то есть, система совместна и имеет единственное решение.

Рассмотрим более содержательные задания:

Пример 14

Составить параметрические уравнения прямой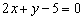

Решение: По условию прямая задана в общем виде. Для того чтобы составить параметрические уравнения прямой, нужно знать её направляющий вектор и какую-нибудь точку, принадлежащую данной прямой.

Найдём направляющий вектор: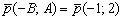

Теперь нужно найти какую-нибудь точку, принадлежащую прямой (подойдёт любая), в этих целях общее уравнение удобно переписать в виде уравнения с угловым коэффициентом: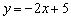

Напрашивается, конечно, точка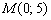

Составим параметрические уравнения прямой:

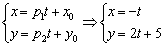
Ответ: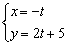

И напоследок небольшая творческая задача для самостоятельного решения.

Пример 15

Составить параметрические уравнения прямой, если известна принадлежащая ей точка 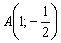и вектор нормали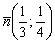

Задачу можно оформить не единственным способом. Одна из версий решения и ответ в конце.

Решения и ответы:

Пример 2: Решение: Найдём угловой коэффициент:

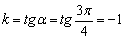
Уравнение прямой составим по точке 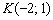и угловому коэффициенту :

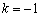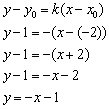
Ответ: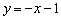

Пример 4: Решение: Уравнение прямой составим по формуле:

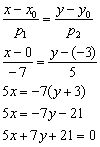
Ответ: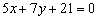

Пример 6: Решение: Используем формулу:

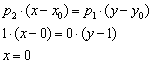
Ответ: 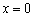(ось ординат)

Пример 8: Решение: Составим уравнение прямой по двум точкам:

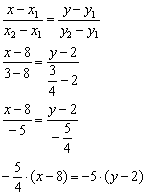
Умножаем обе части на –4:

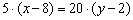
И делим на 5:

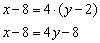
Ответ: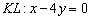

Пример 10: Решение: Используем формулу:

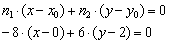
Сокращаем на –2:

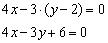
Направляющий вектор прямой: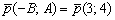
Ответ: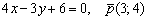

Пример 12:
а) Решение: Преобразуем уравнение:

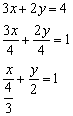
Таким образом:

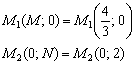
Ответ: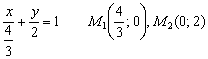

б) Решение: Преобразуем уравнение:

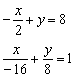
Таким образом:

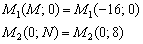
Ответ: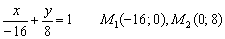

Пример 15: Решение: Сначала составим общее уравнение прямой по точке 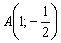и вектору нормали :

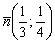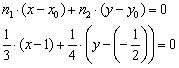
Умножаем на 12:

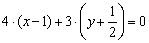
Умножаем ещё на 2, чтобы после раскрытия второй скобки избавиться от дроби:

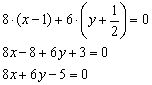
Направляющий вектор прямой: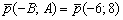
Параметрические уравнения прямой составим по точке 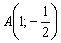и направляющему вектору :
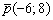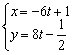
Ответ: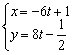

Простейшие задачи с прямой на плоскости.
Взаимное расположение прямых. Угол между прямыми

Продолжаем рассматривать эти бесконечные-бесконечные прямые.

Как определить взаимное расположение двух прямых?
Как построить прямую, параллельную данной?
Как найти точку пересечения двух прямых?
Как построить прямую, перпендикулярную данной?
Как найти расстояние от точки до прямой?
Как построить точку, симметричную относительно прямой?
Как найти расстояние между двумя параллельными прямыми?
Как найти угол между двумя прямыми?

Взаимное расположение двух прямых

Рассмотрим две прямые, заданные уравнениями в общем виде:

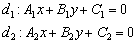
Тот случай, когда зал подпевает хором. Две прямые могут:

1) совпадать;

2) быть параллельными: ;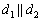

3) или пересекаться в единственной точке: .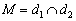

Пожалуйста, запомните математический знак пересечения 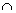, он будет встречаться очень часто. Запись 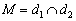обозначает, что прямая 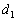пересекается с прямой 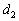в точке .

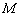Как определить взаимное расположение двух прямых?

Начнём с первого случая:

Две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства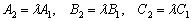

Рассмотрим прямые 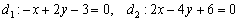и составим три уравнения из соответствующих коэффициентов: 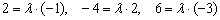. Из каждого уравнения следует, что 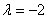, следовательно, данные прямые совпадают.

Действительно, если все коэффициенты уравнения 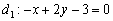умножить на –1 (сменить знаки), и все коэффициенты уравнения 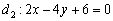сократить на 2, то получится одно и то же уравнение: .

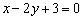Второй случай, когда прямые параллельны:

Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных 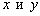пропорциональны: 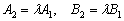, но .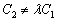

В качестве примера рассмотрим две прямые 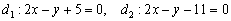. Проверяем пропорциональность соответствующих коэффициентов при переменных :

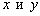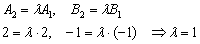
Однако совершенно очевидно, что .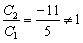

Вывод: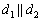

И третий случай, когда прямые пересекаются:

Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных 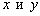НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства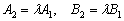

Так, для прямых 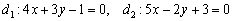составим систему:

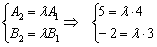
Из первого уравнения следует, что 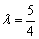, а из второго уравнения: 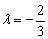, значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных 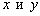не пропорциональны.

Вывод: прямые пересекаются

В практических задачах можно использовать только что рассмотренную схему решения. Она, кстати, весьма напоминает алгоритм проверки векторов на коллинеарность. Но существует более цивилизованная упаковка:

Пример 1

Выяснить взаимное расположение прямых:

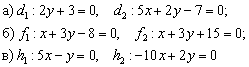
Решение основано на исследовании направляющих векторов прямых:

а) Из уравнений 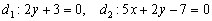найдём направляющие векторы прямых: .

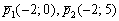Вычислим определитель, составленный из координат данных векторов:
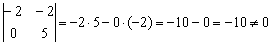, значит, векторы 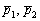не коллинеарны и прямые 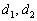пересекаются.

б) Найдем направляющие векторы прямых :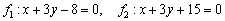

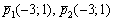
Прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают. Тут и определитель считать не надо.

Очевидно, что коэффициенты при неизвестных 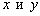пропорциональны, при этом .

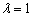Выясним, справедливо ли равенство :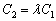

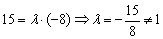
Таким образом,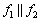

в) Найдем направляющие векторы прямых :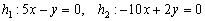

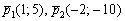
Вычислим определитель, составленный из координат данных векторов:
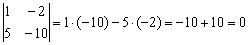, следовательно, направляющие векторы коллинеарны. Прямые либо параллельны, либо совпадают.

Коэффициент пропорциональности «лямбда» можно узнать прямо соотношения коллинеарных направляющих векторов 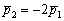. Впрочем, можно и через коэффициенты самих уравнений: .

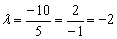Теперь выясним, справедливо ли равенство 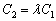. Оба свободных члена нулевые, поэтому:

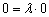
Полученное значение 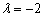удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).

Таким образом, прямые совпадают.

Ответ: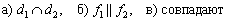

Как построить прямую, параллельную данной?

Пример 2

Прямая задана уравнением 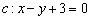. Составить уравнение параллельной прямой, которая проходит через точку .

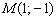Решение: Обозначим неизвестную прямую буквой 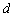. Что о ней сказано в условии? Прямая 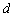проходит через точку 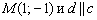. А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для построения прямой «дэ».

Вытаскиваем направляющий вектор из уравнения :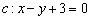

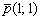
Уравнение прямой 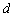составим по точке 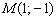и направляющему вектору :

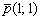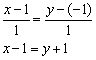
Ответ: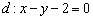

Геометрия примера выглядит незатейливо:

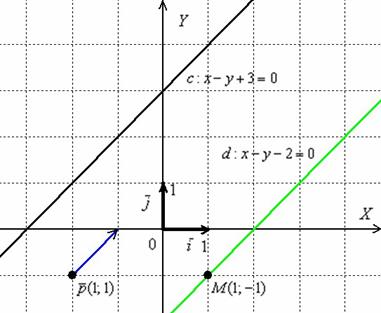
Аналитическая же проверка состоит в следующих шагах:

1) Проверяем, что у прямых 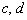один и тот же направляющий вектор (если уравнение прямой не упрощено должным образом, то векторы будут коллинеарны).

2) Проверяем, удовлетворяет ли точка 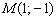полученному уравнению .

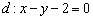Аналитическую проверку в большинстве случаев легко выполнить устно. Посмотрите на два уравнения, и многие из вас быстро определят параллельность прямых безо всякого чертежа.

Примеры для самостоятельного решения сегодня будут творческими.

Пример 3

Составить уравнение прямой, проходящей через точку 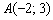, параллельную прямой 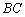, если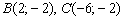

Самый короткий путь – в конце.

Как найти точку пересечения двух прямых?

Если прямые 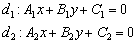пересекаются в точке 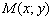, то её координаты являются решением системы линейных уравнений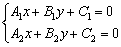

Как найти точку пересечения прямых? Решить систему.

Вот вам и геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще всего) прямые на плоскости.

Пример 4

Найти точку пересечения прямых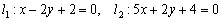

Решение: Существуют два способа решения – графический и аналитический.

Графический способ состоит в том, чтобы просто начертить данные прямые и узнать точку пересечения непосредственно из чертежа:

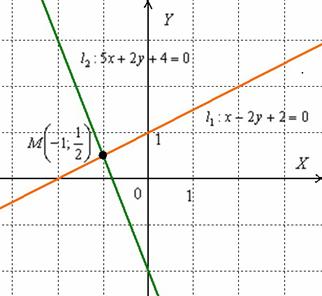
Вот наша точка: 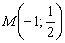. Для проверки следует подставить её координаты в каждое уравнение прямой, они должны подойти и там, и там. Иными словами, координаты точки 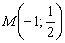являются решением системы 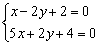. По сути, мы рассмотрели графический способ решения системы линейных уравнений с двумя уравнениями, двумя неизвестными.

Графический способ, конечно, неплох, но существует заметные минусы. Нет, дело не в том, что так решают семиклассники, дело в том, что на правильный и ТОЧНЫЙ чертёж уйдёт время. Кроме того, некоторые прямые построить не так-то просто, да и сама точка пересечения может находиться где-нибудь в тридесятом царстве за пределами тетрадного листа.

Поэтому точку пересечения 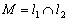целесообразнее искать аналитическим методом. Решим систему:

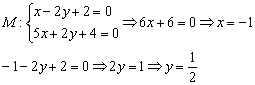
Для решения системы использован метод почленного сложения уравнений.

Ответ: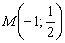

Проверка тривиальна – координаты точки пересечения должны удовлетворять каждому уравнению системы.

Пример 5

Найти точку пересечения прямых 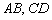в том случае, если они пересекаются.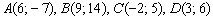

Это пример для самостоятельного решения. Задачу удобно разбить на несколько этапов. Анализ условия подсказывает, что необходимо:
1) Составить уравнение прямой .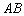
2) Составить уравнение прямой .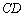
3) Выяснить взаимное расположение прямых .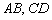
4) Если прямые пересекаются, то найти точку пересечения.

Разработка алгоритма действий типична для многих геометрических задач, и я на этом буду неоднократно заострять внимание.

Полное решение и ответ в конце:

Перпендикулярные прямые. Расстояние от точки до прямой.
Угол между прямыми

Как построить прямую, перпендикулярную данной?

Пример 6

Прямая задана уравнением 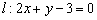. Составить уравнение перпендикулярной прямой 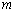, проходящей через точку .

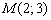Решение: По условию известно, что 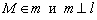. Неплохо бы найти направляющий вектор прямой 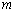. Поскольку прямые перпендикулярны, фокус прост:

Из уравнения 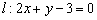«снимаем» вектор нормали: 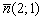, который и будет направляющим вектором прямой .

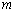Уравнение прямой 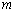составим по точке 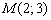и направляющему вектору :

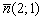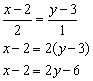
Ответ: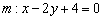

Развернём геометрический этюд:

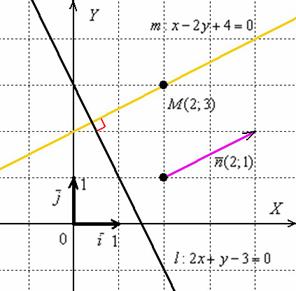
Аналитическая проверка решения:

1) Из уравнений 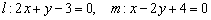вытаскиваем направляющие векторы 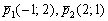и с помощью скалярного произведения векторов приходим к выводу, что прямые действительно перпендикулярны: .

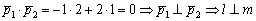Кстати, можно использовать векторы нормали, это даже проще.

2) Проверяем, удовлетворяет ли точка 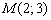полученному уравнению .

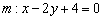Проверку, опять же, легко выполнить устно.

Пример 7

Найти точку пересечения перпендикулярных прямых 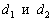, если известно уравнение 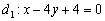и точка .

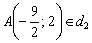Это пример для самостоятельного решения. В задаче несколько действий, поэтому решение удобно оформить по пунктам.

Расстояние от точки до прямой

Расстояние в геометрии традиционно обозначают греческой буквой «р», например: 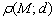– расстояние от точки «м» до прямой «д».

Расстояние от точки 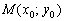до прямой 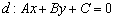выражается формулой

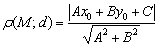
Пример 8

Найти расстояние от точки 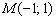до прямой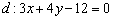

Решение: всё что нужно, это аккуратно подставить числа в формулу и провести вычисления:

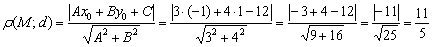
Ответ: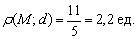

Выполним чертёж:

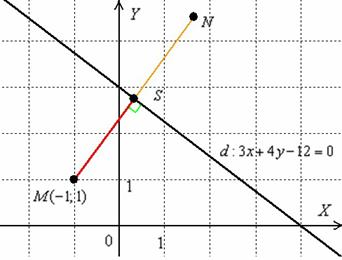
Найденное расстояние от точки до прямой – это в точности длина красного отрезка. Если оформить чертёж на клетчатой бумаге в масштабе 1 ед. = 1 см (2 клетки), то расстояние можно измерить обыкновенной линейкой.

Рассмотрим ещё одно задание по этому же чертежу:

Как построить точку, симметричную относительно прямой?

Задача состоит в том, чтобы найти координаты точки 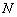, которая симметрична точке 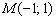относительно прямой 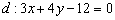. Предлагаю выполнить действия самостоятельно, однако обозначу алгоритм решения с промежуточными результатами:

1) Находим прямую 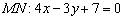, которая перпендикулярна прямой .

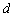2) Находим точку пересечения прямых: .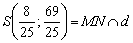

Оба действия подробно разобраны в рамках данного урока.

3) Точка 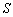является серединой отрезка 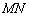. Нам известны координаты середины и одного из концов. По формулам координат середины отрезка находим .

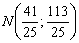Не лишним будет проверить, что расстояние 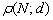тоже равно 2,2 единицам.

Как найти расстояние между двумя параллельными прямыми?

Пример 9

Найти расстояние 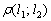между двумя параллельными прямыми

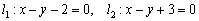
Это очередной пример для самостоятельного решения. Немного подскажу: тут бесконечно много способов решения. Разбор полётов в конце, но лучше постарайтесь догадаться сами, думаю, вашу смекалку удалось неплохо разогнать.

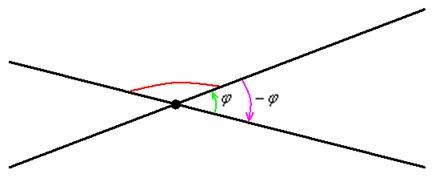
В геометрии за угол между двумя прямыми принимается МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом между пересекающимися прямыми. А считается таковым его «зелёный» сосед 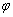или противоположно ориентированный «малиновый» угол .

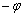Если прямые перпендикулярны, то за угол между ними можно принимать любой из 4-х углов.

Чем отличаются углы 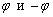? Ориентацией. Во-первых, принципиально важным является направление «прокрутки» угла. Во-вторых, отрицательно ориентированный угол записывается со знаком «минус», например, если .

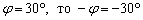Зачем я это рассказал? Вроде бы можно обойтись и обычным понятием угла. Дело в том, что в формулах, по которым мы будем находить углы, запросто может получиться отрицательный результат, и это не должно застать вас врасплох. Угол со знаком «минус» ничем не хуже, и имеет вполне конкретный геометрический смысл. На чертеже для отрицательного угла следует обязательно указывать стрелкой его ориентацию (по часовой стрелке).

Как найти угол между двумя прямыми? Существуют две рабочие формулы:

Пример 10

Найти угол между прямыми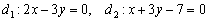

Решение и Способ первый

Рассмотрим две прямые, заданные уравнениями в общем виде:

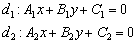
Если прямые не перпендикулярны, то ориентированный угол 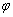между ними можно вычислить с помощью формулы:

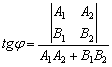
Самое пристальное внимание обратим на знаменатель – это в точности скалярное произведение направляющих векторов прямых:

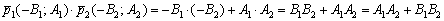
Если 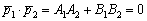, то знаменатель формулы обращается в ноль, а векторы будут ортогональны и прямые перпендикулярны. Именно поэтому сделана оговорка о неперпендикулярности прямых в формулировке.

Исходя из вышесказанного, решение удобно оформить в два шага:

1) Вычислим скалярное произведение направляющих векторов прямых:
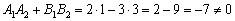, значит, прямые не перпендикулярны.

2) Угол между прямыми найдём по формуле:

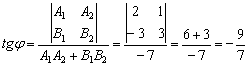
С помощью обратной функции легко найти и сам угол. При этом используем нечётность арктангенса:

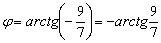
Ответ: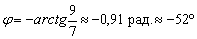

В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью калькулятора.

Ну, минус, так минус, ничего страшного. Вот геометрическая иллюстрация:

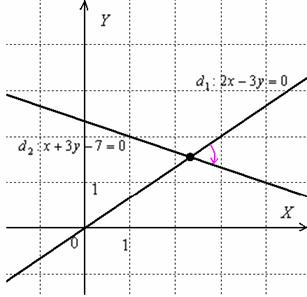
Неудивительно, что угол получился отрицательной ориентации, ведь в условии задачи первым номером идёт прямая 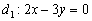и «открутка» угла началась именно с неё.

Если очень хочется получить положительный угол, нужно поменять прямые местами, то есть коэффициенты 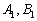взять из второго уравнения 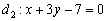, а коэффициенты 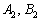взять из первого уравнения 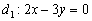. Короче говоря, начать необходимо с прямой .

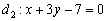Утаивать не буду, сам подбираю прямые в том порядке, чтобы угол получился положительным. Так красивее, но не более того.

Для проверки решения можно взять транспортир и измерить угол.

Способ второй

Если прямые заданы уравнениями с угловым коэффициентом 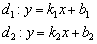и не перпендикулярны, то ориентированный угол 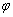между ними можно найти с помощью формулы:

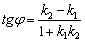
Условие перпендикулярности прямых выражается равенством 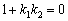, откуда, кстати, следует очень полезная взаимосвязь угловых коэффициентов перпендикулярных прямых: 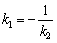, которая используется, в частности при нахождении уравнения нормали.

Алгоритм решения похож на предыдущий пункт. Но сначала перепишем наши прямые в нужном виде:

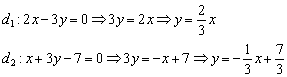
Таким образом, угловые коэффициенты: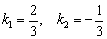

1) Проверим, будут ли прямые перпендикулярны:
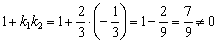, значит, прямые не перпендикулярны.

2) Используем формулу:

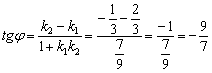
Ответ: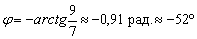

Второй способ уместно использовать тогда, когда уравнения прямых изначально заданы с угловым коэффициентом. Следует отметить, что если хотя бы одна прямая параллельна оси ординат, то формула не применима вообще, поскольку для таких прямых угловой коэффициент не определён

Есть и третий способ решения. Идея состоит в том, чтобы вычислить угол между направляющими векторами прямых:

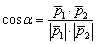
Здесь уже речь идёт не об ориентированном угле, а «просто об угле», то есть результат заведомо будет положительным. Загвоздка состоит в том, что может получиться тупой угол (не тот, который нужен). В этом случае придётся делать оговорку, что угол между прямыми – это меньший угол, и из «пи» радиан (180-ти градусов) вычитать получившийся арккосинус.

Пример 11

Найти угол между прямыми .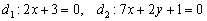

Это пример для самостоятельного решения. Попробуйте решить его двумя способами.

Решения и ответы:

Пример 3: Решение: Найдём направляющий вектор прямой :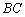

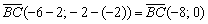
Уравнение искомой прямой составим по точке 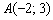и направляющему вектору 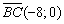. Так как одна из координат направляющего вектора нулевая, уравнение 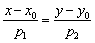перепишем в виде:

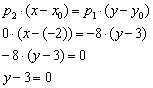
Ответ: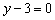

Пример 5: Решение:
1) Уравнение прямой 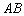составим по двум точкам :

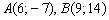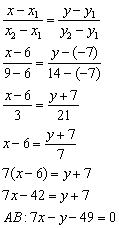
2) Уравнение прямой 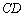составим по двум точкам :

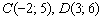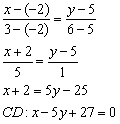
3) Соответствующие коэффициенты при переменных 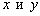не пропорциональны: 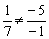, значит, прямые пересекаются.
4) Найдём точку :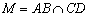

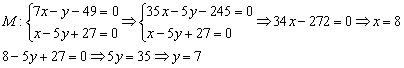
Примечание: здесь первое уравнение системы умножено на 5, затем из 1-го уравнения почленно вычтено 2-ое.
Ответ: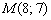

Пример 7: Реше