Уравнения, допускающие понижение порядка

7.1. Уравнение вида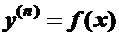

Решение уравнения означает отыскание функции по ее производной 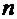-го порядка.

При каждом интегрировании производной ее порядок на

единицу понижается: .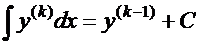

Интегрируя последовательно 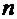раз, получаем (при каждом интегрировании добавляется очередная произвольная постоянная):

;

;

…

.

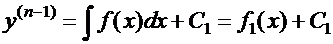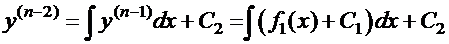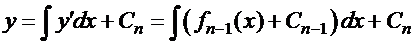Таким образом, найденная функция 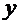, в соответствии с определением общего решения, зависит от 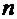произвольных постоянных.

Пример.Для уравнения третьего порядка 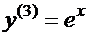найдем общее решение, а затем частное решение, удовлетворяющее начальным условиям .

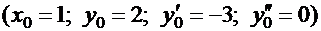Последовательные интегрирования дают:

;

;

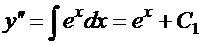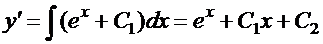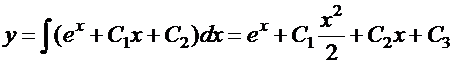— общее решение.

Подставляя начальные условия в полученные выражения для , получаем систему трех линейных уравнений с тремя неизвестными :

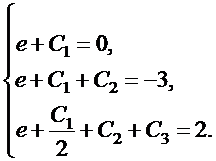
Отсюда: 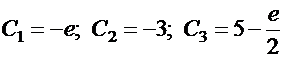, так что решение задачи Коши имеет вид: .

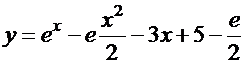7.2. Уравнение, не содержащее явно неизвестную функцию y

Рассмотрим уравнение второго порядка вида 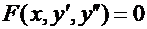, не содержащее явно искомую функцию .

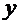Введем новую неизвестную функцию 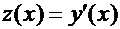. Тогда 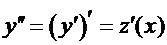, и уравнение принимает вид: 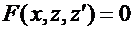. Это уравнение первого порядка. Если найдено его общее решение 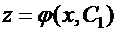, то возвращаясь к исходной неизвестной функции 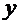, получаем 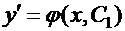, так что 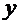находится интегрированием:

.

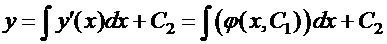Аналогичным образом можно понизить на единицу порядок не содержащего явно 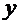уравнения .

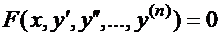Пример. 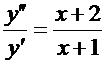. Полагая 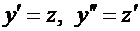, приходим к уравнению с разделяющимися переменными относительно новой неизвестной функции :

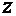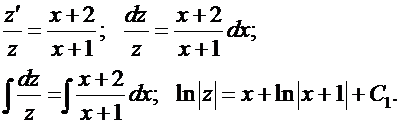
Ограничимся случаем 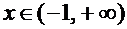, , 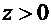что означает строгое возрастание искомой функции 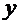(так как 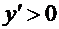). Тогда

,

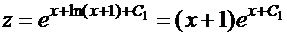или

.

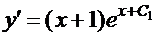Наконец, интегрируя по частям, получаем общее решение:

.

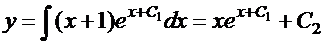7.3. Уравнение, не содержащее явно независимую переменную x

Рассмотрим уравнение второго порядка вида 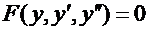, не содержащее явно независимую переменную .

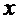Будем предполагать 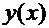строго монотонной функцией. Тогда существует обратная функция 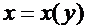, и производные 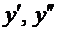можно рассматривать как сложные функции независимой переменной :

.

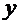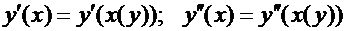Введем новую неизвестную функцию 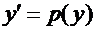. По правилу дифференцирования сложной функции

,

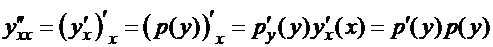так что исходное уравнение второго порядка переходит в уравнение первого порядка относительно новой неизвестной функции :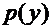

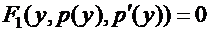. (13)

Если найден общий интеграл уравнения (13)

,

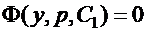то, заменяя в нем 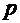на 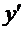, приходим к уравнению первого порядка относительно исходной неизвестной функции :

.

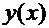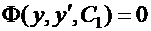Таким образом, решение уравнения второго порядка сводится к последовательному решению двух уравнений первого порядка.

Пример. Рассмотрим уравнение 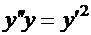. Полагаем 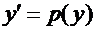; тогда 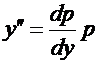. Исходное уравнение преобразуется к виду: 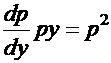. Ограничиваясь случаем 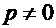, получаем уравнение с разделяющимися переменными:

.

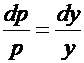Откуда

.

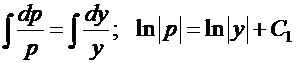Произвольную константу интегрирования удобно записать в виде 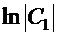, поскольку логарифмическая функция принимает все значения от 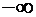до 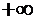. Тогда

.

.

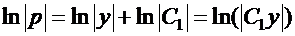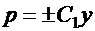Поскольку здесь постоянный множитель при , записанный в виде 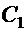, принимает, как и множитель 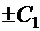, все вещественные значения, можно записать: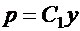

Возвращаемся к исходной неизвестной функции :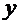

—

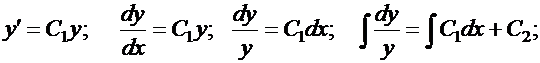
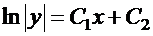общий интеграл.