Глава 2: Линейные системы дифференциальных уравнений.

ЛЕКЦИЯ 8:

Системы вида 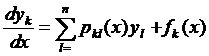, называются линейными.

Будем предполагать, что 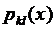, и 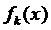непрерывны в интервале 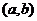. Согласно теореме Пикара система имеет единственное решение 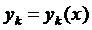, удовлетворяет начальным условиям 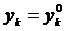при 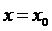, , 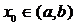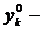произвольные.

Решение определено в интервале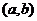

Особых решений линейная система (1) не имеет.

Если 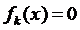, , то система (1) называется однородной 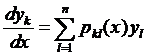, (2)

Свойства решений однородной системы.

1. Если однородная система имеет комплексное решение 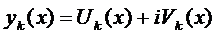, , 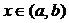(3), то она имеет два вещественных решения 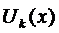и , .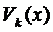

2. Если 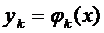, 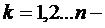решение однородной системы (20, то

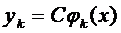, (4) также является решением системы (2), где С – произвольная постоянная.

3. Пусть имеется 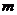решений системы (2):

,

,

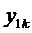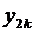… (5)

,

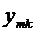Первый индекс обозначает номер решения, а второй означает номер функции.

Линейная комбинация 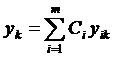, (6) также является решением системы (2).

Результат подстановки 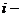ого решения в систему (2) имеет вид:

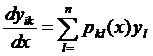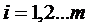, , (7).

Тогда свойство 3. доказывается следующим образом:

,

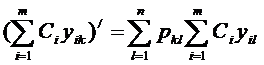
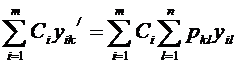учитывая (7), получаем тождество.

Определение:

систем функций

,

,

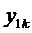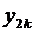… (8)

,

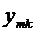называется линейно независимыми в интервале 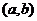, если не существует чисел 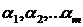не равных одновременно нулю, при которых для всего интервала 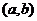выполнялось бы соотношение 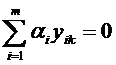, (9)

Очевидно, что если одна из систем (8) равна нулю в интервале 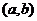, то эти

системы функций линейно зависимыми в .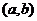

Введём в рассмотрение определитель :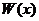

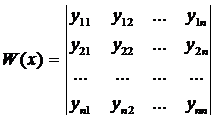(10)

Этот определитель называется определителем Вронского или вронскианом.

Теорема 1:

Если 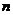систем функций

,

,

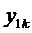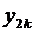… (11)

,

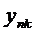линейно независимыми в интервале 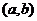, то .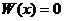

Так как систем функций (11) линейно независимыми, то справедливо соотношение 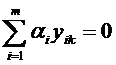, , 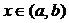(12), где не все 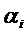равны нулю.

Система (12) является линейной и однородной относительно 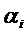и имеет ненулевое решение. Следовательно, определитель системы (12) равен нулю, т.е. .

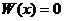Теорема 2:

Если 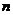систем функций

,

,

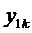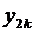… (11)

,

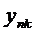системы (2) линейно независимыми в интервале 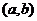, то их вронскиан не обращается в нуль ни в одной точке.

Предположим обратное, что существует точка 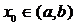, где .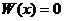

Составим следующую систему:

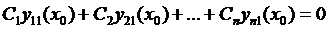
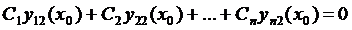
…… (13)

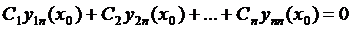
определитель системы (13) равен нулю, следовательно, существует ненулевое решение.

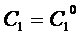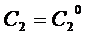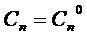, ,…, (14)

Запишем выражение 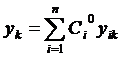, (15)

(15) является решением системы, кроме этого

, ,…,

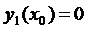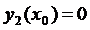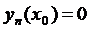
На основании теоремы Пикара решение (15) может быть только ненулевым, т.е. 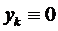, или 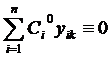, т.е. решения системы (2) линейно независимыми в интервале 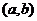, что противоречит условию теоремы.

Из теорем 1. и 2. следует следующее утверждение:

Для линейной независимыми 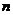решений системы (2) в интервале 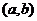,необходимо и достаточно, чтобы вронскиан был отличен от нуля хоть в одной точке этого интервала, что подтверждает формула Остроградского –

Лиувилля.

Формула Остроградского – Лиувилля.

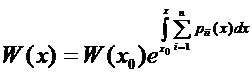
Для доказательства этой формулы найдем производную от вронскиана(по столбцам)

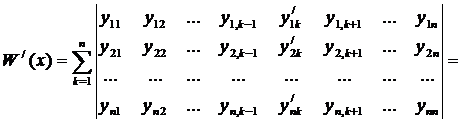
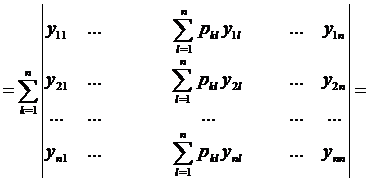
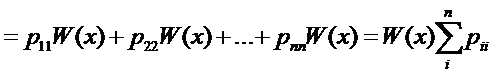(17)

Итак, 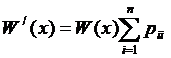(18) решение (18) в форме Коши

.
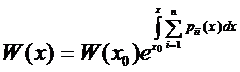