Раздел 4. СПЕКТРАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ

4.1.Дискретное преобразование Фурье

В данном разделе мы рассмотрим один из способов описания циклических кодов, основанный на использовании дискретного преобразования Фурье (ДПФ) кодовых последовательностей, заданных над конечным полем 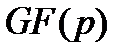. Данный подход позволяет в ряде случаев найти альтернативные методы кодирования и декодирования циклических кодов.

В поле комплексных чисел ДПФ вектора 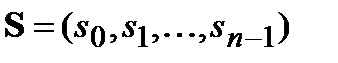с комплексными компонентами определяется как вектор 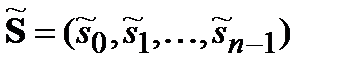, компоненты которого вычисляются согласно соотношению

.

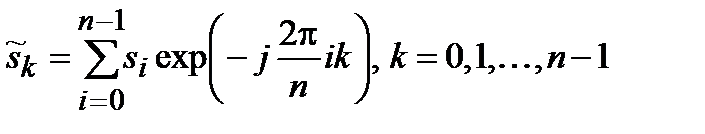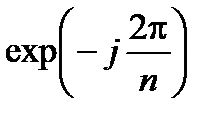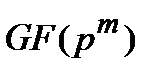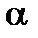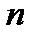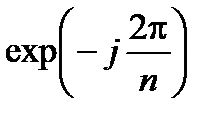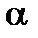Ядром преобразования Фурье является , которое является корнем n–й степени из единицы в поле комплексных чисел. В конечном поле элемент порядка также является корнем n–й степени из единицы. Тогда, проводя аналогию между и , можно ввести следующее определение.

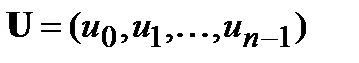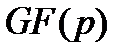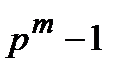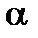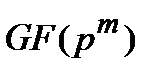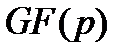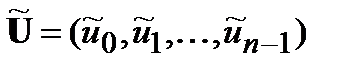Пусть – вектор над , где n делит при некотором m и пусть – элемент мультипликативного порядка n в расширенном поле . Тогда ДПФ над полем вектора является вектор с элементами 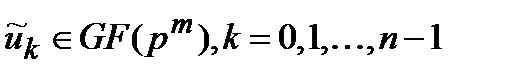, задаваемыми равенствами

(4.1)

,

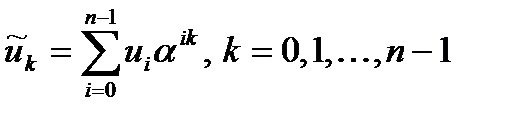или в матричном представлении

.

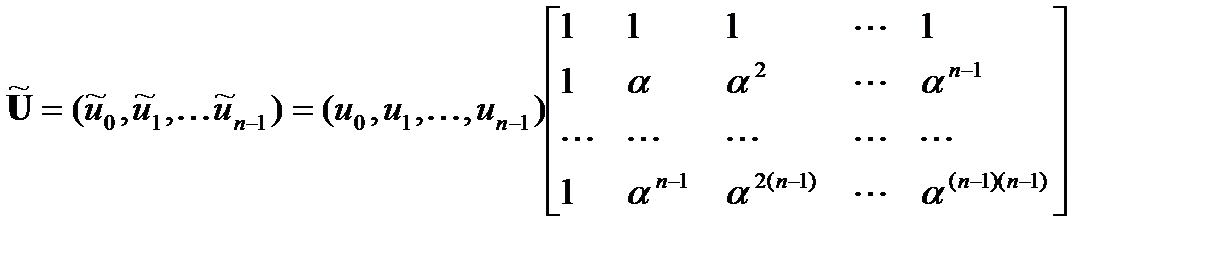Учитывая ранее указанную аналогию, дискретный индекс i естественно назвать дискретным временем, а вектор – временной функцией (последовательностью) или сигналом. Аналогично, индекс k можно назвать дискретной частотой, а вектор 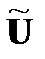– частотной функцией (последовательностью) или спектром. 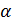называется ядром преобразования, а матрица в правой части равенства – матрицей Фурье.

Если спектр определяется прямым ДПФ, то с помощью обратного ДПФ по спектру может быть определен сам сигнал, т.е. компоненты вектора

.

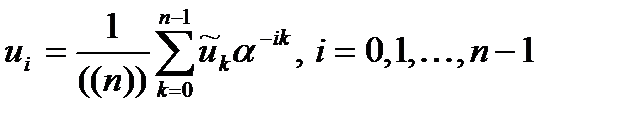Следует также отметить, что если ДПФ 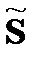вещественнозначной временной функции 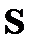является комплексным, то аналогично при преобразовании в поле Галуа временной функции , элементы которой принадлежат полю 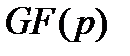, ее спектр 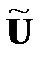лежит в расширенном поле .

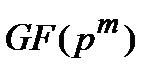Преобразование Фурье обладает рядом замечательных свойств, которые переносятся и на случай преобразования в конечных полях.

Теорема 4.1.1. (Теорема о свертке)Пусть 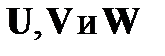– временные последовательности, причем 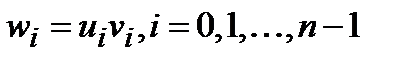. Тогда компоненты ДПФ 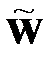могут быть определены как

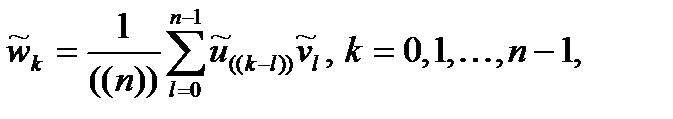
где двойные скобки означают, что индекс вычисляется в арифметике по модулю n.

Доказательство: Вычислим преобразование Фурье вектора с компонентами вида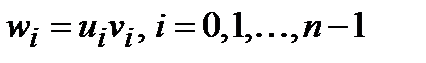

.

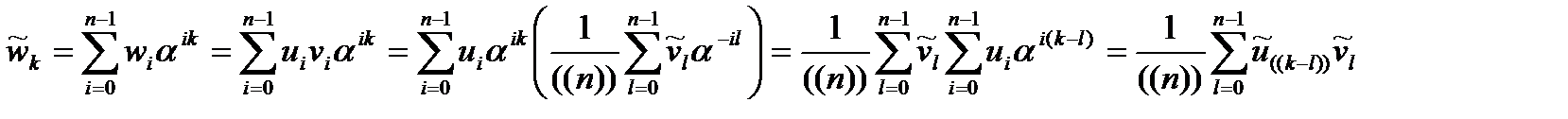Можно сформулировать и обратную теорему, поменяв местами временную и частотную области.

Теорема 4.1.2.Пусть 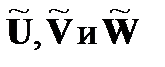– частотные последовательности, причем 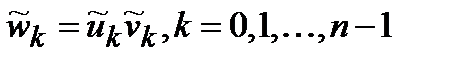. Тогда компоненты вектора могут быть определены как

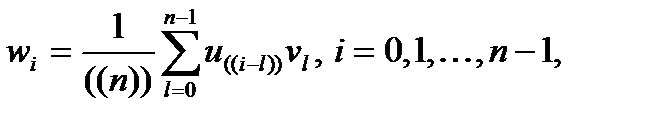
где двойные скобки означают, что индекс вычисляется в арифметике по модулю n.

Отметим также, что выбор 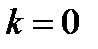в теореме о свертке приводит к формуле типа равенства Парсеваля

.

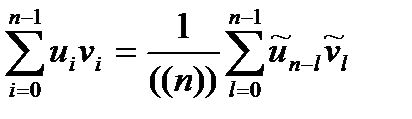Замечание. Основываясь на этом свойстве ДПФ, возможен альтернативный вариант описания циклических кодов. Любое кодовое слово циклического кода может быть представлено в несистематическом виде как

,

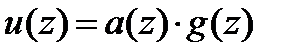где 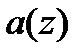– информационный, а 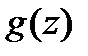– проверочный полиномы. Во временной области коэффициенты кодового полинома определяются циклической сверткой коэффициентов информационного и порождающего полиномов

,

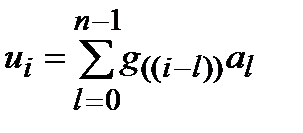так что в частотной области, согласно теореме 4.1.2, операция кодирования может быть осуществлена покомпонентным перемножением спектров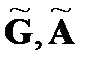

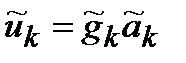
и последующим вычислением обратного ДПФ для спектра кодового слова.

Теорема 4.1.3. (Свойство сдвига)Если последовательност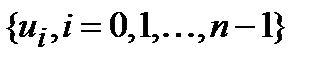и и 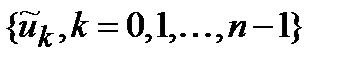являются парой преобразования Фурье, то парами преобразований Фурье являются также 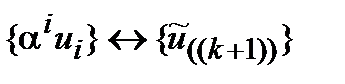и .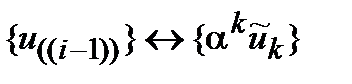

Доказательство осуществляется непосредственной подстановкой.

В том случае, когда кодовому вектору 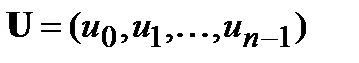сопоставляется полином 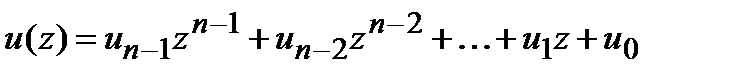, он может быть преобразован в полином 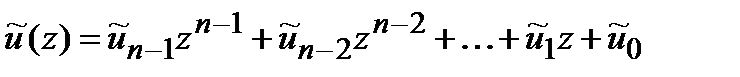, коэффициенты которого отвечают спектральным компонентам ДПФ в поле Галуа вектора , а сам полином называется спектральным (или ассоциированным) с 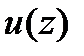многочленом. Следующая теорема устанавливает, что свойства спектра тесно связана с корнями многочленов.

Теорема 4.1.4.

(i). Элемент 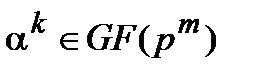является корнем полинома 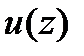тогда и только тогда, когда k–й частотный компонент 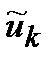равен нулю.

(ii). Элемент 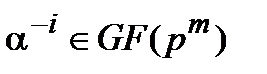является корнем многочлена 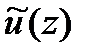тогда и только тогда, когда i–й временной компонент 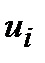равен нулю.

Доказательство утверждения (i) очевидно, поскольку из непосредственной подстановки корня в полино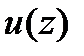м имеем

.

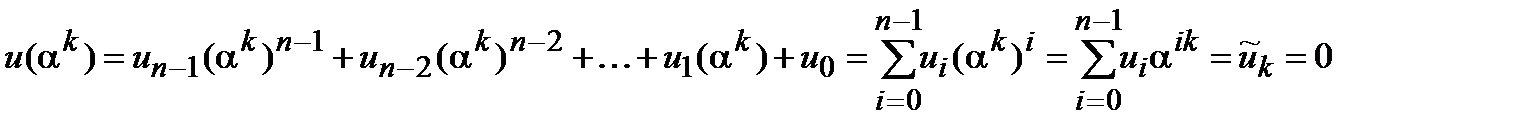Аналогичным образом доказывается и утверждение (ii).

На основании приведенной теоремы можно сделать следующее заключение. Поскольку любой кодовый многочлен содержит в качестве множителя порождающий многочлен, то корни порождающего полинома являются и корнями кодового. Тогда, согласно теореме 4.1.4, корням порождающего многочлена 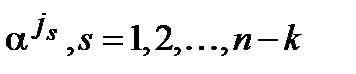будут соответствовать нулевые спектральные компоненты кодовых слов на позициях 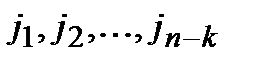. Следовательно, можно дать следующее альтернативное определение циклического кода. Циклическим кодом 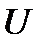называется множество таких слов над конечным полем 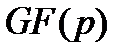, у которых все спектральные компоненты, принадлежащие заданному множеству т.н. проверочных частот 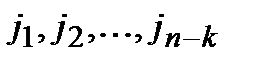равны нулю

Кодовое слово кода Р-С длины 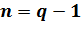и его спектр лежат в одном поле 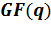.Кодирование кода Рида-Соломона в частной области можно осуществить следующим образом: какие либо 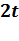последовательных координат полагаются равными нулю, в остальных 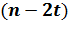координатах записываются информационные символы. Например, информационный вектор может быть такой: 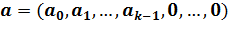.Кодовый вектор, соответствующий информационному вектору, определяется как ДПФ вектора 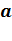с ядром α. Координаты кодового вектора задаются по правилу 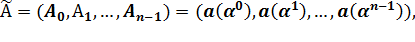так как каждая компонента 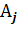вычисляется как значение многочлена a(x) в точке 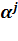: 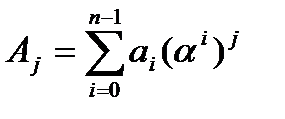. Если a(x) – многочлен из информационной области, A(x) – многочлен из кодовой области, тогда дискретное преобразование Фурье с ядром α (прямое) переводит многочлен из информационной области в кодовую, а дискретное преобразование Фурье с ядром 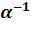(обратное) переводит многочлен из кодовой области в информационную 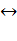а(х) А(х), 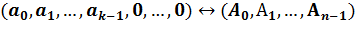.