Принципы обнаружения и исправления ошибок

Пусть для передачи сообщений используется некоторый код длины 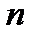и объема 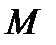. Это означает, что на вход дискретного канала поступает одна из последовательностей 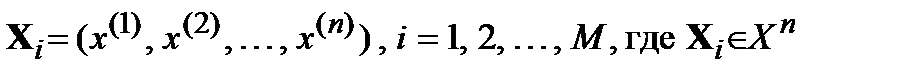, называемая кодовым словом. На приемной стороне наблюдается некоторая выходная последовательность (вектор наблюдений) 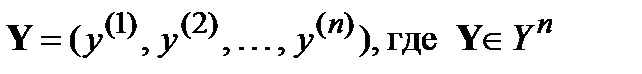. Процедуру решения о том, произошла ли ошибка при передаче кодовой последовательности или нет, можно описать следующим алгоритмом. 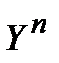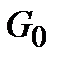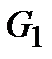Все множество разбивается на две области и , причем область 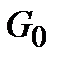образована кодовыми последовательностями, а 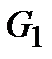– запрещенными комбинациями. Очевидно, что если наблюдаемая последовательность 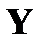, полученная в результате трансформации каналом некоторой кодовой комбинации 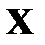, оказывается в области 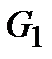, то принимается решение об обнаружении ошибок в принятой последовательности. Если же наблюдаемая последовательность окажется в области 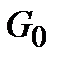, то принимается решение о безошибочной передаче информации.

Естественно возникает вопрос о том, а все ли ошибки могут быть обнаружены? Предположим, что алфавит входных 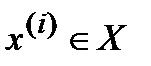и выходных 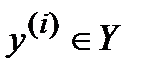символов одинаков, и его объем равен 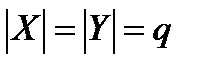. Тогда объем кода, а значит и мощность множества 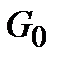, составляют величину 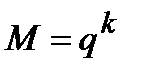, а число запрещенных комбинаций (или мощность множества 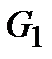) определится как 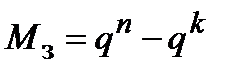. При передаче по каналу связи M кодовых комбинаций возможны 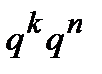их переходов в принятые наблюдения 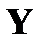, из которых только 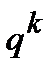будут правильными, тогда как остальные 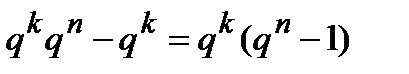переходов сопровождаются искажениями. Как уже указывалось, решение об обнаружение ошибок в принятой последовательности принимается всякий раз, когда она оказывается в области 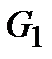. Подобной ситуации отвечают 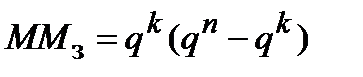переходов и, значит, общее число обнаруживаемых ошибок составляет величину 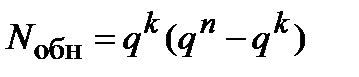, что еще раз свидетельствует о возможности обнаружения ошибок только при условии 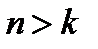, т.е. при введении избыточных символов. Сравнение же общего количества ошибок 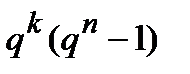с числом обнаруживаемых 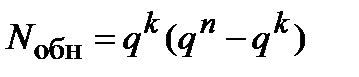демонстрирует, что не все ошибки удается зафиксировать. Последнее объясняется тем, что переход одной кодовой комбинации в другую под действием канальных помех невозможно обнаружить, причем общее количество подобных переходов составит величину .

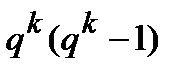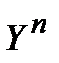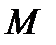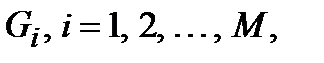
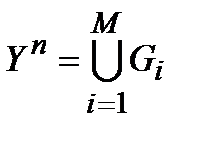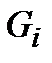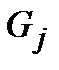Аналогичным образом реализуется и процедура исправления ошибок. Отличие заключается лишь в том, что все множество разбивается теперь на (по числу передаваемых сообщений) решающих областей , причем и при 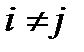не пересекаются, а в каждую область решения 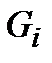включается только одна кодовая последовательность. Если оказывается, что вектор наблюдений 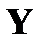принадлежит j-й области, т.е. 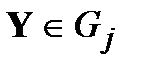, то принимается решение о том, что было передано слово 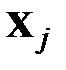и, значит, канальные ошибки, вызвавшие трансформацию 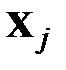в 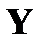, будут исправлены. Поскольку области решений не перекрываются, то общее число исправляемых ошибок определяется числом запрещенных комбинаций, распределяемых между M решающими областями. Следовательно, 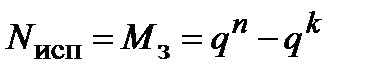и, значит, как и в случае обнаружения ошибок, их исправление возможно лишь при 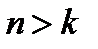, т.е. при введении избыточности.