Истинная диаграмма растяжения

Почти все механические характеристики, которыми оцениваются свойства материала (см. пункт «Механические характеристики»), определяют по отношению к начальным размерам об­разца: площади A₀, длине l₀. При этом не учитывают изменений размеров образца в процессе его деформиро­вания – уменьшения площади и увеличения длины. В этом заключается их условность. Если пере­строить ма­шинную диа­грамму F – Dl в координаты «напряжение σ – относи­тельная де­формация e» σ = f(e) (рис. 1.2), то послед­няя в некото­ром мас­штабе повто­рит машин­ную диа­грамму. Истин­ные S напря­жения начи­нают отли­чаться в бóльшую сторону от условных (технических) σ с первого момента нагружения, т. к. уменьшается площадь поперечного сечения образца. Истинная диа­грамма растяжения S = φ(e) – функция неубывающая. Существенные расхождения диаграмм истинных и условных напряжений становятся заметными с началом пластической деформации (см. рис. 1.2). Считают, что до достижения нагрузкой своего максимального значения F_max (см. рис. 1.2, напряжение σ_в) образец деформируется равномерно (см. рис. 1.2, сечение m): истинное напряжение S_m постоянно во всех сечениях, диаметр d_m < d₀ и одинаков по всей расчетной длине образца.

На участке местного сужения в шейке (см. рис. 1.2, сечение n) минимальный диаметр образца значительно меньше начального d_n << d₀. Истинные напряжения распределяются не равномерно по длине, как на участке упрочнения, а становятся значительно больше условных S_n >> σ_n. В момент разрушения превышение S_к над σ_в может достигать 30…50 %.

Рис. 1.2. Изменение конфигурации образца на различных стадиях деформирования (а); распределение истинных напряжений по длине образца при равномерном «m» и сосредоточенном «n» деформировании (б); диаграммы истинных S = φ(e) и условных σ = f(e) напряжений (в)

В научных целях обычно используют истинную диаграмму, построенную в координатах S – ψ или S – e, где ψ – относительное сужение поперечного сечения (1.1); e – относительная логарифмическая деформация e = ln (ℓ/ℓ₀). Истинная диаграмма более информативна, что имеет немалое значение для правильного понимания основных закономерностей сопротивления пластической деформации. Истинные напряжения точнее отражают поведение материала под нагрузкой, чем технические. Их используют в существующих и вновь создаваемых методиках расчёта при сложном напряжённом состоянии, действии циклических нагрузок и др.

Механические характеристики

Механические характеристики, оценивающие прочностные свойства материала, называются характеристиками прочности, оценивающие пластические свойства – характеристиками пластичности.

А. Характеристики прочности

К характеристикам прочности относятся:

- предел текучести физический;

- предел текучести условный;

- временное сопротивление (предел прочности);

- предел пропорциональности;

- предел упругости.

Предел текучести физический σ_т – напряжение, при котором образец деформируется без увеличения растягивающей нагрузки. Вычисляется физический предел текучести по формуле:

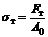, (1.2)

где F_т – нагрузка, соответствующая площадке текучести (см. рис. 1.1); A₀ – начальная площадь поперечного сечения образца.

Предел текучести условный σ_0,2 – напряжение, при котором остаточное удлинение достигает 0,2 % от расчётной длины образца.

Порядок определения:

1) рассчитать допуск на величину остаточного удлинения Dl_0,2 = 0,002·ℓ₀ – где ℓ₀ – начальная расчётная длина образца (база тензометра);

2) в масштабе оси деформаций машинной диаграммы из начала координат отложить отрезок Dl_0,2 (см. рис. 1.3, а);

3) параллельно участку упругой деформации провести прямую до пересечения с диаграммой растяжения;

4) измерить ординату F_0,2 на диаграмме растяжения и вычислить нагрузку, соответствующую точке пересечения прямой с диаграммой;

5) рассчитать условный предел текучести

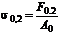. (1.3)

Временное сопротивление (предел прочности)[6] σ_в – напряжение, соответствующее наибольшей нагрузке F_max, предшествующей разрыву образца. Определяется делением усилия F_max на первоначальную площадь поперечного сечения образца (см. рис. 1.1):

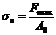. (1.4)

Теперь обратим особое внимание на характеристики сопротивления малым пластическим деформациям. Предел упругости – это наибольшее напряжение, до которого материал не получает остаточных деформаций. Предел пропорциональности – это наибольшее напряжение, превышение которого вызывает отклонение от закона Гука.

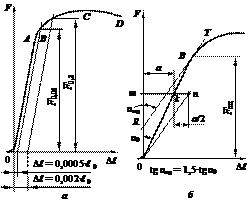
Рис. 1.3. Схемы к определению предела упругости и условного предела текучести (а), а также предела пропорциональности (б)

Анализ диаграмм растяжения, записанных с высокой точностью измерения деформаций и напряжений, показывает, что отступление от закона Гука (прямой σ = Е∙ε) для многих материалов наступает уже на ранних стадиях нагружения. Поэтому численные значения пределов пропорциональности и упругости зависят от условно принятой степени приближения, с которой начальный участок можно рассматривать как прямую. Стандартом принято пределом пропорциональности считать напряжение, при котором так называемый «мгновенный» модуль упругости Е = dσ/dε (модуль упругости в текущий момент испытания; он соответствует тангенсу угла наклона между касательной к диаграмме и осью ε) уменьшается от своего начального значения на 50 %. Обе характеристики – предел упругости и предел пропорциональности – близки по смыслу и, как установлено ещё Баушингером^[7] в 1879–1886 гг., различие между ними настолько мало, что в технических задачах их можно считать практически совпадающими.

Предел упругости σ_0,05 – напряжение, при котором остаточное удлинение достигает 0,05 % длины участка рабочей части образца, равного базе тензометра.

Методика определения такая же, как и для условного предела текучести, но допуск на остаточную деформацию в 4 раза меньше (см. рис. 1.3, а).

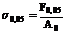. (1.5)

Предел пропорциональности σ_пц – напряжение, при котором отклонение от линейной зависимости между нагрузкой и удлинением достигает такой величины, что тангенс угла наклона между касательной к кривой «нагрузка – удлинение» в точке F_пц и осью нагрузок увеличивается на 50 % от своего значения на упругом (линейном) участке.

Порядок определения:

1) на произвольной высоте диаграммы в пределах упругого участка проводят прямую mn, параллельную оси абсцисс (см. рис. 1.3, б);

2) измеряют длину a отрезка mk между осью ординат и диаграммой растяжения; справа от диаграммы откладывают отрезок kn = a/2;

3) из начала координат в точку n проводят луч 0n и параллельно ему касательную RT к диаграмме растяжения (при этом tgα_пц будет на 50 % превышать tgα);

4) ордината точки B касания с диаграммой определит искомую нагрузку F_пц. Предел пропорциональности вычисляют по формуле:

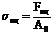. (1.6)

Истинное сопротивление разрыву S_к – напряжение, вычисляемое путём деления разрушающего усилия F_к (см. рис. 1.1, ордината точки D) на действительную площадь сечения в шейке A_к:

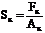. (1.7)

Площадь A_к вычисляется по диаметру d_к (рис. 1.4).