Понятие соответствия между множествами.

Соответствием между элементами множества Х и элементами множества Y называется любое подмножество декартова произведения этих множеств.

Взаимно однозначные соответствия.

Взаимно однозначным соответствием между множествами X и Y называется такое соответствие, при котором каждому элементу множества X сопоставляется единственный элемент множества Y и каждый элемент множества Y соответствует только одному элементу множества X.

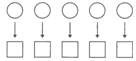
Если множества конечны, то отношение взаимно-однозначно только, если они содержат одинаковое количество элементов.

Если между множествами можно установить взаимно-однозначное соответствие, то такие множества называются равномощными.

Определение числовой функции.

Числовой функцией называется такое соответствие между числовым множеством X и множеством R действующих чисел, при котором каждому числу их множества X сопоставляется единственное из множества R.

(Множество X называют областью определения функции.

Множество R – это множество действительных чисел.)

Способы задания функций.

1. при помощи уравнения-формулы

2. при помощи таблицы

3. с помощью графика

Примеры числовых функций из начального курса математики, заданных при помощи:

См. учебник Петерсон 4 кл. 3 ч.

а) таблицы; (стр. 70, №3 Тема: График движения)

Заполни таблицу и построй график движения Сиропчика и Незнайки.

t ч						t
S км

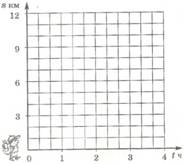
v = 3 км/ч

б) выражения с переменной; (см. учебники 4 кл.)

Вычисли значения выражений:

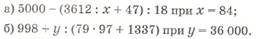
в) формулы.

Постройте график функций y=5-x, если ее область определения X такова:

- X={0,1,2,3,4,5};

- X=[0;5].

3 ВОПРОС:Персон 4 кл,3ч
6. Определения отношений на множестве. Отношения эквивалентности и их связь с разбиением множества на классы. Примеры заданий из учебников математики для начальных классов, при выполнении которых происходит разбиение на классы с помощью отношения.

Определения отношений на множестве.

Рассматриваемое отношения между двумя элементами, называется бинарным;

между тремя элементами – тернарным.

Отношениемна множестве или отношением между элементами множества называется, любое подмножество декартова произведения множества самого на себя.

Отношение – это есть множество упорядоченных пар.

Отношение обозначается заглавными буквами латинского алфавита (конечными).

Свойства отношений:
1) Отношение R, заданное на множестве X, обладает свойством рефлексивности, если каждый элемент данного множества вступает в отношение R с самим собой. На множестве натуральных чисел рефлексивными свойствами обладают отношения кратности, равенства, делимости.
2) Отношение R, заданное на множестве X, обладает свойством симметричности, если из того, что какой-либо элемент х из множества Х вступает в отношение R с элементом у из множества Х, следует, что элемент у вступает в отношение R с элементом х. R – равенство на множестве.
3) Отношение R, заданное на множестве X, обладает свойством антисимметричности, если для различных элементов х и у из множества X из того, что элемент х вступил в отношение R с элементом у следует, что элемент у в отношение R с элементом х не вступает. Отношения кратности, делимости, больше (меньше) на …
4) Отношение R, заданное на множестве X, обладает свойством транзитивности, если из того, что элемент х из множества Х входит в отношение R с элементом у из множества У и элемент у входит в отношении R с элементом z из множества Х, следует, что элемент х входит в отношение R с элементом z. Отношения кратности, делимости, параллельности между прямыми.