Сущность плавания по дуге большого круга
Плавание между двумя точками 1 и 2 с координатами φ1; λ1 и φ2; λ2 можно совершить двумя путями: по локсодромии (постоянным курсом, но более длинным путем) и по ортодромии (кратчайшим путем, но переменными курсами). Разница в длине пути будет существенной при плавании на большие расстояния (трансокеанские переходы) и при близких значениях широт точек 1 и 2. Локсодромия и ортодромия совпадают при курсах, близких к 0° и 180°, а также на любых курсах вблизи экватора. Будем решать задачу на сфере (без учета сфероидичности Земли).
Задача расчета плавания по локсодромии состоит в определении локсодромического курса К.л и длины локсодромии SЛ.
Переход судна, следующего постоянным курсом, совершается до локсодромии. Плавание по локсодромии очень удобно, так как судно весь переход удерживают на постоянном курсе. Однако локсодромия не является кратчайшим расстоянием между выбранными пунктами перехода.
При небольших переходах разность расстояний по локсодромии и по ортодромии настолько незначительна, что ею пренебрегают и плавание осуществляют по локсодромии.
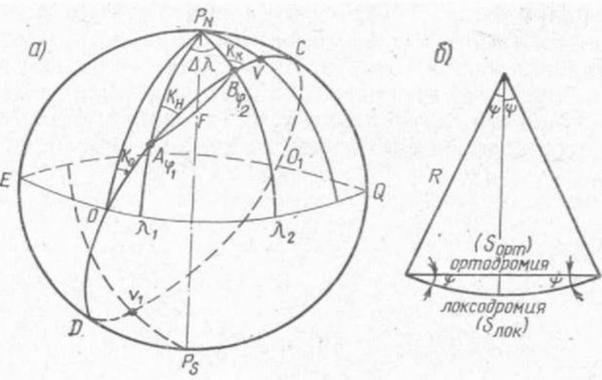
Например, при плавании из пункта А в пункт В (рис. 112, а) необходимо проложить путь судна по дуге А В большого круга ABCD, проведенного через пункты отхода и прихода, так как кратчайшим расстоянием между двумя точками на шаре будет меньшая из дуг большого круга, проходящая через эти точки.
Если же судно при переходе из пункта A в В будет идти не по дуге большого круга, а по локсодромии AFB или по дуге какого-либо малого круга, проходящего через те же точки, то оно будет проходить большее расстояние.
Выигрыш в длине пути при плавании по локсодромии и ортодромии определяется сравнением расстояний между точками по локсодромии и ортодромии.
Из формул письменного счисления длина пути по локсодромии определяется
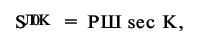
или при К ~ 90°(270°)
Длину дуги большого круга (АВ ) — расстояние по ортодромии можно рассчитать по формуле косинуса стороны из сферического треугольника PNA В:
Для небольших расстояний ортодромические поправки w в конечных пунктах можно принять одинаковыми. Тогда длину ортодромии можно рассчитать так:
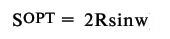
Расчеты показывают, что плавание по дуге большого круга даст сокращение расстояния на 0,5% и более
Когда плавание происходит по ортодромии, курс во время перехода будет непрерывно изменяться в пределах от КH до КK (см. рис. 112, а), т. е. от направления дуги большого круга в пункте отхода, называемого начальным курсом КH, до направления ее в пункте прихода, называемого конечным курсом КK.
Любой большой круг, проведенный на поверхности земного шара, пересекает линию экватора в двух точках О и О1 и имеет по одной точке (V и V1) в каждом полушарии с наибольшей широтой — кратчайшим расстоянием от земных полюсов.
Точка на дуге большого круга, находящаяся в кратчайшем расстоянии от земного полюса (имеющая наибольшую широту), называется вертексом данной дуги большого круга.