Запись алгебраических выражений

Как упоминалось ранее, алгебраические выражения составляются из констант, переменных, обращений к функциям с помощью знаков арифметических операций и скобок. При этом следует соблюдать ряд правил и рекомендаций.

1 Необходимо учитывать приоритет операций (см. таблицу 1): сначала выполняется умножение (знак *) и деление (знак /), затем сложение и вычитание.

Все знаки арифметических операций, даже те, которые при корректной математической записи ставить не принято (например, как при записи произведения ab = a×b), необходимо указывать при составлении выражения на Pascal. Изменить порядок выполнения операций можно с помощью скобок, как показано в таблице 9.

Таблица 9 − Учет приоритета операций посредством скобок

Математическое выражение	Запись на языке Pascal	Возможные ошибки
	(a−b)/(c+d)	Отсутствие скобок изменит смысл выражения: a-b/c+d ~
	(sin(x)+y)/(x*y)	1 Пропущенный знак умножения означает указание на новую (возможно, несуществующую) переменную xy: (sin(x)+y)/xy 2 Неправильно расставленные или пропущенные скобки изменят смысл выражения: (sinx+y)/(x*y) ~ введено новое имя sinx; (sin(x)+y)/x*y ~ − изменен смысл

2 Аргументы сложных функций (функция функции) необходимо заключать в скобки (таблица 10).

Таблица 10 − Pascal-код сложных функций

Математическое выражение	Запись на языке Pascal	Возможные ошибки
	sqrt(abs(sin(x)));	Потеря скобок или неправильный порядок расположения функций
	sqr(ln(2*x));	Потеря скобок, неправильный порядок следования функций, потеря знака умножения
	exp(2*sqr(cos(x)));	Неправильный порядок следования функций, потеря знака умножения или скобок

3 При построении на языке Pascal сложных арифметических выражений целесообразно использовать вспомогательные переменные. Например, при кодировании формулы

(1)

можно ввести промежуточную переменную f 1 и только после этого записать оператор присваивания для вычисления f :

f1:=sin(x)/cos(x);

f:=(1+sqr(f1))/(1-2*sqr(f1));

4 Для записи на языке Pascal экспоненциальной функции e^x, где e » 2,718281828 − основание натурального логарифма, используется ее представление в виде exp(x). Ряд примеров приведен в таблице 11:

Таблица 11 − Pascal-код экспоненциальной функции

Математическое выражение	Запись на языке Pascal
	exp(a+b)
	exp(1)
	exp(–1)

5 Определенные трудности возникают при записи степенных и показательных выражений, например, 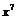, или . Pascal-код в таких случаях составляется с учетом формул элементарной математики:

, (2)

. (3)

Примеры приведены в таблице 12.

Таблица 12 − Pascal-код степенных и показательных выражений

Математическое выражение	Альтернативная математическая запись	Запись на языке Pascal
		exp(x/2*ln(a+b))
		exp(1/3*ln(a/b))

6 Необходимо учитывать область определения функций, к которым в выражении происходит обращение. Такие ошибки легче предотвратить, чем исправлять, так как они не обнаруживаются компилятором. Например, для выражения , записанного на языке Pascal в виде

exp(17*ln(x)),

при выполнении программы возникнет ошибка при отрицательных значениях переменной х. Поэтому его лучше записать в форме

sqr(sqr(sqr(sqr(x))))*x,

исключающей подобную ошибку.

Два других примера представлены в таблице 13.

Таблица 13 − Учет области определения функций

Математическое выражение	Запись на языке Pascal	Альтернативная запись на языке Pascal
	exp(1/8*ln(x));	sqrt(sqrt(sqrt(x)))
	exp(1/5*ln(x));	ifx>0theny:= exp(1/5*ln(x)) else ifx<0 then y:=- exp(1/5*ln(abs(x))) elsey:=0;

7 Не следует забывать о скорости выполнения операций и рациональной записи выражений. Арифметические операции в порядке возрастания их времени выполнения располагаются так: сложение и вычитание, умножение и деление. Поэтому в некоторых случаях целесообразно заменять умножение сложением или использовать функции или процедуры вместо операций сложения и умножения. Например, выражение x*x лучше записать как sqr(x), а вместо оператора присваивания x:=x + 1 использовать обращение к процедуре inc(x).

Пример 2. Запишите на языке Pascal выражение .

Решение.

~ x*(x*(x*(2*x-3)+5)-1)+7.