Повторение испытаний. Формула Бернулли. Асимптотические формулы

Пусть по отношению к событию А проводится n испытаний. Введем события: А_k – событие А осуществилось при k-том испытании, k=1,2,…, n. Тогда 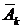- противоположное событие (событие А неосуществилось при k-том испытании, k=1,2,…, n).

Испытания называются однотипными по отношению к событию А, если вероятности событий А₁, А₂, …, А_n совпадают: Р(А₁)=Р(А₂)= …=Р(А_n) (т.е. вероятность появления события А в одном испытании постоянна во всех испытаниях). Очевидно, что в этом случае вероятности противоположных событий также совпадают: .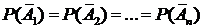

Испытания называются независимыми по отношению к событию А, если события А₁, А₂, …, А_n независимы. В этом случае

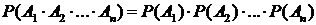
При этом равенство сохраняется при замене любого события А_k на .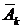

Пусть по отношению к событию А проводится серия из n однотипных независимых испытаний. Ведем обозначения: р – вероятность осуществления события А в одном испытании; q – вероятность противоположного события. Таким образом, Р(А_к)=р, 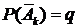для любого k и p+q=1.

Вероятность того, что в серии из n однотипных независимых испытаний событие А осуществится ровно k раз (0≤k≤n), вычисляется по формуле:

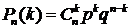(14)

Равенство (14) называется формулой Бернулли.

Вероятность того, что в серии из n однотипных независимых испытаний событие А осуществится не менее k₁раз и не более k₂раз, вычисляется по формуле:

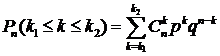(15)

Применение формулы Бернулли при больших значениях n приводит к громоздким вычислениям, поэтому в этих случаях лучше использовать другие формулы – асимптотические.

Формула Пуассона

Если число испытаний n велико, а вероятность осуществления события в одном испытании р мала, то вместо формулы Бернулли используют приближенную формулу Пуассона:

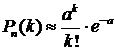(16)

Здесь 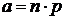- среднее число появлений события в n испытаниях. Формула Пуассона дает хорошее приближение для формулы Бернулли при .

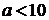Аналог формулы (15) имеет:

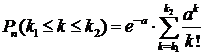(17)

Формулы Муавра-Лапласа

Если число испытаний n велико, а вероятность осуществления события в одном испытании р не слишком мала (так что 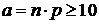), то формула Пуассона дает значительную погрешность. В этом случае используют другую приближенную формулу – локальную формулу Муавра-Лапласа:

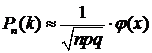, (18)

где 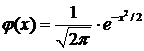и 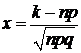. Значения функции 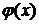можно найти в специальных таблицах, которые приведены в литературе по теории вероятностей. Отметим, что функция 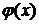является четной, поэтому таблицы ее значений приведены только для .

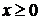Аналог формулы (15) в данном случае имеет вид:

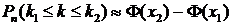, (19)

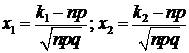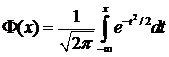где и - функция Лапласа. Формула (19) носит название интегральной формулы Муавра-Лапласа. Значения функции Лапласа также приведены в специальных таблицах. Отметим, что часто таблицы составлены для функции 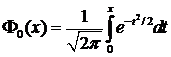и необходимо учитывать формулу связи: 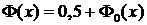. Функция 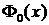является нечетной, поэтому таблицы ее значений приведены только для 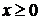. Для функции 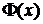справедливо равенство: .

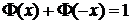Задание 7. Вероятность заболевания гриппом во время эпидемии равна0,4. Найти вероятность того, что из 6 сотрудников фирмы заболеют

1) ровно 4 сотрудника;

2) не более 4-х сотрудников.

Решение. 1) Очевидно, что для решения данной задачи применима формула Бернулли, где n=6; k=4; р=0,4; q=1-р=0,6. Применяя формулу (14), получим: .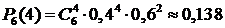

2) Для решения данной задачи применима формула (15), где k₁=0 и k₂=4. Имеем:

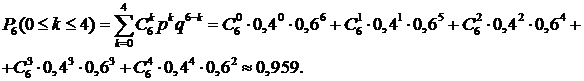
Следует заметить, что эту задачу проще решать, используя противоположное событие – заболело более 4-х сотрудников. Тогда с учетом формулы (7) о вероятностях противоположных событий получим:

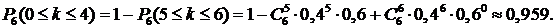
Задание 8. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено

1) ровно три изделия;

2) менее трех изделий.

Решение. 1) Поскольку вероятность р=0,002 повреждения изделия мала, а число изделий n=500 велико, и 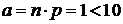, можно воспользоваться формулой Пуассона. Применяя формулу (16) при k=3, получим: .

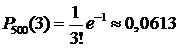2) Для решения второй задачи применима формула (17), где k₁=0 и k₂=2. Имеем: .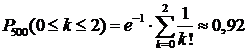

Задание 9. К магистральному водопроводу подключены 160 предприятий, каждое из которых с вероятностью 0,7 в данный момент осуществляет забор воды. Найти вероятность того, что в данный момент забор воды осуществляют

1) ровно 100 предприятий;

2) не менее 80 и не более 120 предприятий.

Решение. 1) В данном случае вероятность р=0,7 осуществления забора воды одним предприятием не мала, а число предприятий n=160 велико, и 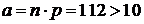. Поэтому для решения задачи надо воспользоваться локальной формулой Муавра-Лапласа (18). Имеем: n=160; k=100; р=0,7; q= 0,3. Вычисляем значение x: 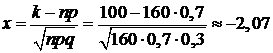и находим значение 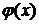по таблице: 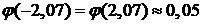. Тогда по формуле (18) получим:

.

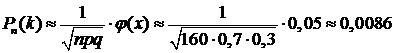2) Для решения второй задачи применима интегральная формула Муавра-Лапласа (19), где k₁=80 и k₂=100. Вычисляем значения x₁ и x₂:

; .

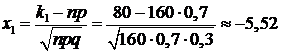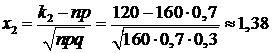С учетом свойств функции Лапласа, перечисленных ранее, и таблиц значений функции Лапласа находим:

.

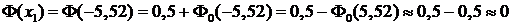
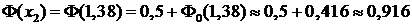Тогда по формуле (19) получим: .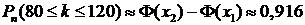

Случайные величины

Переменная Х называется случайной величиной по отношению к данному испытанию, если в результате испытания она принимает одно из своих возможных числовых значений, но какое именно, до испытания неизвестно.

Случайные величины принято обозначать большими буквами латинского алфавита, например, X, Y, Z, а их возможные значения - соответствующими малыми буквами – x, y, z.

Функция F(x) действительной переменной x, -∞<x<∞, определяемая формулой

F(x) = P(X<x) ,

называется функцией распределения случайной величины Х.

Свойства функциираспределения:

1) 0≤ F(x) ≤1, -∞<x<∞;

2) F(-∞) =0, F(+∞) =1;

3) F(x) - неубывающая функция на всей оси;

4) F(x) непрерывна слева, т.е. .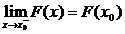

Различают случайные величины дискретного типа (ДСВ) и случайные величины непрерывного типа (НСВ).

Случайная величина Х называется дискретной случайной величиной, если множество ее возможных значений есть числовая последовательность (конечная или бесконечная).

Распределением дискретной случайной величиной называется функция, областью определения которой являются все возможные значения рассматриваемой величины, а областью значений - вероятности соответствующих значений. Распределение ДСВ удобно представлять в виде таблицы:

Возможные значения	x1	x2	x3	….	xn
Вероятности	p1	p2	p3	….	pn

Здесь p_i = P(X=x_i), 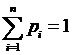(условие нормировки).

Случайная величина Х называется непрерывной случайной величиной, если ее возможные значения заполняют некоторый промежуток (конечный или бесконечный) числовой оси.

Плотностью распределения НСВ Х называется функция f(x), которая определена при всех x, -∞<x<∞, и удовлетворяет условиям:

1) f(x) ≥0 во всей области определения;

2) .

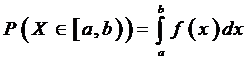Свойства плотности распределения НСВ:

1) Если f(x) -плотность распределения НСВ Х и F(x) – функция распределенияэтойслучайной величины, то

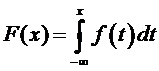
2) Еслиплотность распределения f(x) есть функция непрерывная при 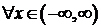, то

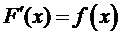
3) 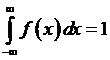(условие нормировки).

Числовые характеристики случайных величин

Математическим ожиданием случайной величины X называется действительное число M(X), определяемое в зависимости от типа случайной величины Х формулой:

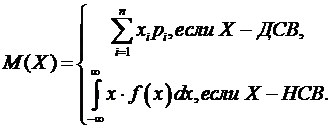
Две случайные величины Х и Y называются независимыми, если для любых x и y имеет место равенство P(X<x, Y<y)= P(X<x) ·P(Y<y).

Свойства математического ожидания:

1) M(C)=C, где C-const;

2) M(CX)=CM(X);

3) M(X±Y)=M(X) ±M(Y), где Х и Y – любые случайные величины;

4) M(X·Y)=M(X) ·M(Y), если Х и Y –независимые случайные величины.

Дисперсией случайной величины Х называется неотрицательное число D(X), определяемое в зависимости от типа случайной величины Х формулой:

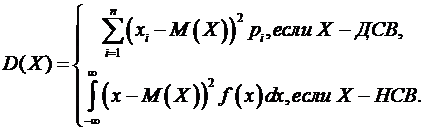
Свойства дисперсии:

1) D(C) =0, где C - const;

2) D(CX)=C² D(X);

3) D(X±Y)=D(X)+D(Y), если Х и Y –независимые случайные величины.

Теорема. Дисперсия любой случайной величины Х равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания:

D(X) = M(X²) - M² (X)

Нормальное распределение

Непрерывная случайная величина Х имеет нормальное распределение с параметрами m, σ (σ >0), если ее плотность определяется формулой:

, .

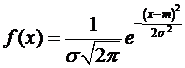Задание 1. Задан закон распределения дискретной случайной величины Х:

xi	-1
pi	0,1	0,2	0,4	0,2	0,1

Найти M(X), M(3X+4), D(X), D(4X- 5).

Решение.

1) По определению математического ожидания:

.

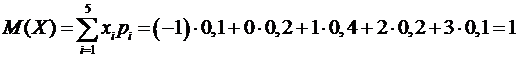2) По свойствам математического ожидания:

.

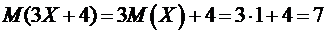3) По теореме о вычислении дисперсии:

.

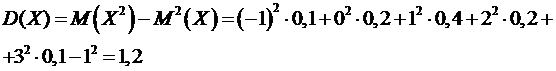4) По свойствам дисперсии:

.

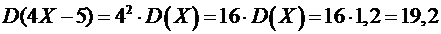Задание 2. Для НСВ Х задана функция распределения:

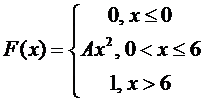
Найти A, f(x), M(X), M(3X-2), D(X), D(2X+4), P(X<5), P(X>1), P(-1<X <3).

Решение.

1) По свойству плотности распределения:

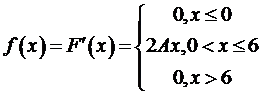
Воспользуемся теперь условием нормировки: 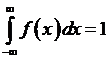. Имеем: 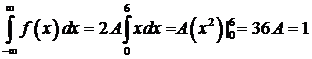, следовательно, .

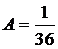2) Тогда плотность распределения случайной величины Х:

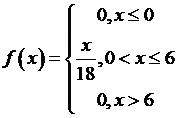
3) По определению математического ожидания:

.

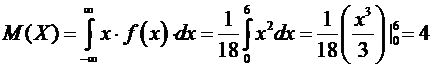4) По свойствам математического ожидания:

.

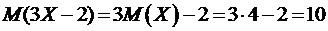5) По теореме о вычислении дисперсии:

.

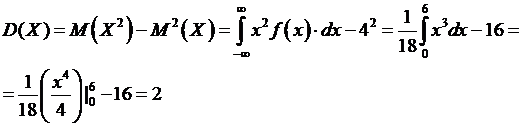6) По свойствам дисперсии:

.

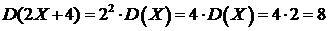7) По определению плотности распределения:

.

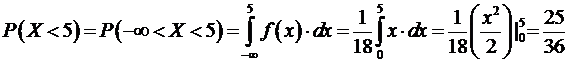8) Аналогично:

.

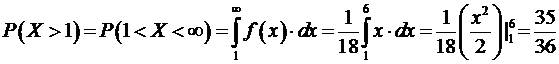9) И, наконец,

.
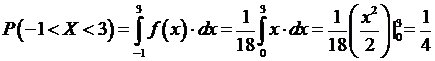