Понятие вероятности события. Классическое определение вероятности

События A и B называются несовместными по отношению к данному испытанию, если их произведение есть событие невозможное по отношению к данному испытанию.

Вероятностью события A по отношению к данному испытанию называется число P(A), удовлетворяющее следующим условиям:

1) 0 ≤ P(A) ≤ 1

2) P(U)=1, P(V)=0

3) Если A и B – несовместные события, то P(A+B)=P(A)+P(B).

Классическое определение вероятности события

Назовем событие A благоприятствующим событию B, если из осуществления события A следует осуществление события B. В противном случае событие A называется не благоприятствующим событию B.

Предположим, что система событий Е₁, Е₂, …, Е_n образует полную систему элементарных событий по отношению к данному испытанию. Это означает, что указанная система событий по отношению к данному испытанию является:

1) полной (т.е. сумма всех этих событий есть событие достоверное);

2) несовместной (т.е. любые два события несовместны);

3) равновозможной (т.е. возможность осуществления любого из этих событий не имеет преимуществ перед возможностью осуществления любого другого).

Пусть событие A таково, что любое из элементарных событий Е₁, Е₂, …, Е_n либо благоприятствует событию A, либо не благоприятствует. Вероятностью события A при рассматриваемом испытании называется число, равное отношению числа m элементарных событий, благоприятствующих событию A, к общему числу n элементарных событий:

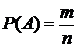(1)

Нетрудно убедиться, что классическое определение вероятности события удовлетворяет всем условиям определения вероятности, данного выше.

Задание 1. Имеется 40 карточек, на которых написаны числа от 1 до 40. Карточки перемешаны и наугад выбирается одна карточка. Какова вероятность того, что число, написанное на карточке, делится на 4?

Решение. Испытанием в данной задаче является выбор карточки. Общее число элементарных событий n=40 (число карточек). Событию А благоприятствуют m=10 элементарных событий (число карточек с числами, делящимися на 4). Тогда согласно классическому определению вероятности события имеем: .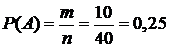

Для вычисления вероятности события необходимо найти числа m и n. В некоторых случаях для этого используют формулы комбинаторики.

Элементы комбинаторики

Конечное множество называется упорядоченным, если его элементы каким-либо образом пронумерованы, т.е. указан порядок следования элементов.

Пусть дано конечное множество M, состоящее из m элементов. Размещением из m элементов по n элементов называется любое упорядоченное подмножество, содержащее n элементов, из множества M, содержащего m элементов. Таким образом, различные размещения отличаются друг от друга либо составом входящих в них элементов, либо порядком их расположения.

Число размещений из m элементов по n элементов обозначается 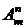и вычисляется по формуле:

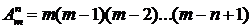(2)

Перестановками из n элементов называются различные упорядочения конечного множества, состоящего из n элементов. Таким образом, различные перестановки отличаются друг от друга лишь порядком элементов. Число перестановок обозначается P_n и вычисляется по формуле:

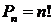(3)

Сочетанием из m элементов по n элементов называется любое подмножество, содержащее n элементов, из множества M, содержащего m элементов. Таким образом, различные сочетания отличаются друг от друга только составом входящих в них элементов.

Число сочетаний из m элементов по n элементов обозначается 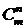и вычисляется по формуле:

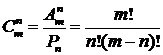(4)

Задание 2. Восемь книг расставлены на полке случайным образом. Найти вероятность того, что две определенные книги окажутся поставленными рядом.

Решение. Воспользуемся классическим определением вероятности события. Общее число элементарных событий в данном случае равно n=P₈=8! - число способов расставить 8 книг на полке (число перестановок из 8 элементов). Событию А благоприятствуют 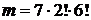элементарных событий (число способов расставить 8 книг так, чтобы 2 определенные книги оказались поставленными рядом). Тогда, согласно классическому определению вероятности события, имеем: .

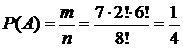Задание 3. На карточках разрезной азбуки напечатаны буквы з, а, д, а, ч, а. Карточки тщательно перемешаны. Найти вероятность того, что на 4-х вынутых по одной и расположенных в ряд карточках, можно будет прочесть слово «дача».

Решение. Общее число элементарных событий в данном случае равно 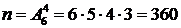- число способов вынуть 4 карточки из имеющихся 6 (число размещений из 6 элементов по 4 элемента). Событию А благоприятствуют 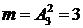элементарных событий (число способов получить слово «дача»). Тогда согласно классическому определению вероятности события имеем: .

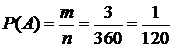Задание 4. Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек для участия в соревнованиях. Найти вероятность того, что среди них будет 2 женщины.

Решение. Общее число элементарных событий в данном случае равно 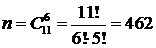- число способов выбрать 6 человек из имеющихся 11 (число сочетаний из 11 элементов по 6 элементов). Событию А благоприятствуют 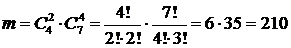элементарных событий (число способов выбрать 6 человек так, чтобы среди них было 2 женщины, а 4 - мужчины). Тогда согласно классическому определению вероятности события имеем: .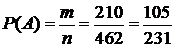