Понятие неопределеннного интеграла, свойства
| Определение 1: | Функция  называется первообразнойфункцией для функции называется первообразнойфункцией для функции 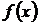 на промежутке на промежутке 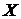 , если в каждой точке , если в каждой точке 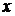 этого промежутке этого промежутке  . . |
| Определение 2: | Совокупность всех первообразных для функции 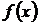 на промежутке на промежутке 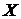 называется неопределенным интегралом от функции называется неопределенным интегралом от функции 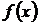 и обозначается и обозначается  . Таким образом: . Таким образом:  , где , где  - некоторая первообразная для - некоторая первообразная для 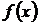 , с – произвольная постоянная. , с – произвольная постоянная. |
В частности:  .
.
Свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.:
 .
.
Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.:
 .
.
2. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.:
 .
.
3. Постоянный множитель можно выносить за знак интеграла, т.е.:
 , где
, где
 - некоторое число.
- некоторое число.
4. Интеграл от алгебраической суммы функции равен алгебраической сумме интегралов от слагаемых функций:
 .
.
5. Если числитель подынтегральной дроби есть производная от знаменателя, то интеграл равен логарифму модуля знаменателя:
 .
.
Таблица интегралов от основных элементарных функций
 ; ; |  ; ; |
 ; ; |
 ; ; |  ; ; |
 ; ; |  ; ; |
 ; ; |  ; ; |
 ; ; |  ; ; |
 ; ; |  ; ; |
 ; ; |  ; ; |
 ; ; |  . . |
Определенный интеграл. Основные свойства
Если  - первообразная функция от
- первообразная функция от 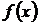 , т.е.
, т.е.  , то
, то  .
.
Эта формула вычисления определенного интеграла называется формулой Ньютона-Лейбница.
Геометрический смысл. Если функция 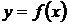 непрерывна на отрезке
непрерывна на отрезке  и внутри этого отрезка всюду неотрицательна, то определенный интеграл
и внутри этого отрезка всюду неотрицательна, то определенный интеграл  представляет собой в декартовой системе координат площадь криволинейной трапеции
представляет собой в декартовой системе координат площадь криволинейной трапеции  (см. рис. 12), ограниченной графиком подинтегральной функции
(см. рис. 12), ограниченной графиком подинтегральной функции 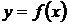 , осью
, осью  и двумя прямыми
и двумя прямыми  .
.
Рис. 12
Свойства определенного интеграла
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5. Если  постоянная, то
постоянная, то  ;
;
6.  .
.
Основные методы интегрирования
Основными методами интегрирования являются непосредственное интегрирование при помощи основных свойств неопределенного и определенного интеграла и таблицы интегралов, метод подстановки (замены переменной) и интегрирование по частям.
Метод непосредственного интегрирования
Метод состоит в том, что с помощью алгебраических преобразований подынтегральная функция приводится к табличной или их сумме. Рассмотрим этот метод на примерах.
Примеры:
1. 
 .
.
2. 
 .
.
3. 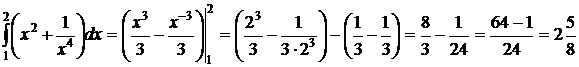
Метод подстановки
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла или интеграла, берущегося тем или иным известным приемом. Такой метод называется методом подстановки, а также методом замены переменной.
Рассмотрим функцию 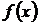 , где
, где  , тогда:
, тогда:
 (3.1)
(3.1)
Формула (3.1) называется формулой замены переменной в неопределенном интеграле.
После нахождения интеграла  надо вместо
надо вместо  подставить его выражение через
подставить его выражение через 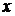 . В определенном интеграле возврат к переменной
. В определенном интеграле возврат к переменной 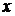 не обязателен, но в этом случае при замене переменной необходимо изменить пределы интегрирования, т. е. воспользоваться формулой:
не обязателен, но в этом случае при замене переменной необходимо изменить пределы интегрирования, т. е. воспользоваться формулой:
 .
.
Примеры.
1.  .
.
Обозначим  , тогда
, тогда  и, следовательно,
и, следовательно,  .
.
 .
.
2.  .
.
3.  .
.
4.
| | Полагаем  . Дифференцируя это соотношение, находим . Дифференцируя это соотношение, находим |
 |  , откуда , откуда  . Находим теперь новые пределы интеграла. Для этого из соотношения . Находим теперь новые пределы интеграла. Для этого из соотношения  определяем определяем |
| | значения  при при  и и  при при  . Итак, имеем . Итак, имеем |

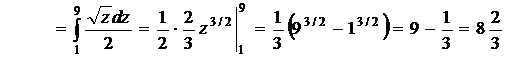
В приведенных выше примерах метод замены переменной быстро привел к цели. Однако удачный выбор новой переменной обычно представляет известные трудности. Для их успешного преодоления необходимо хорошо владеть техникой дифференцирования, уметь «прикидывать», что даст та или иная подстановка, и твердо знать табличные интегралы.
Интегрирование по частям
Пусть функции  и
и  непрерывно дифференцируемы на некотором промежутке, тогда:
непрерывно дифференцируемы на некотором промежутке, тогда:
 . (3.2)
. (3.2)
Формулу (3.2) обычно записывают в виде:
 . (3.2*)
. (3.2*)
Для определенного интеграла она такова:
 .
.
Эти формулы называются формулами интегрирования по частям. Правильнее было бы назвать их формулами частичного интегрирования. При известных 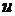 и
и  они сводят нахождение интеграла от
они сводят нахождение интеграла от  после частичного интегрирования к нахождению интеграла от
после частичного интегрирования к нахождению интеграла от  . Иногда удается функции
. Иногда удается функции 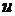 и
и  выбрать так, что новый интеграл либо сам является табличным, либо сводится к табличным интегралам уже известными методами.
выбрать так, что новый интеграл либо сам является табличным, либо сводится к табличным интегралам уже известными методами.
При этом следует учитывать, что за 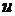 принимается функция, которая дифференцированием упрощается, а за
принимается функция, которая дифференцированием упрощается, а за  - та часть подынтегрального выражения, содержащая
- та часть подынтегрального выражения, содержащая  , интеграл от которой известен или может быть найден.
, интеграл от которой известен или может быть найден.
Так, при вычислении интегралов вида  ,
,  ,
,  за
за 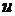 следует принять многочлен
следует принять многочлен  , а за
, а за  - соответственно выражения -
- соответственно выражения -  ,
,  ,
,  .
.
При вычислении интегралов вида  ,
,  ,
,  за
за  следует принять выражение
следует принять выражение  , а за
, а за 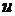 - соответственно функции
- соответственно функции  ,
,  ,
,  .
.
Примеры.
1.  . Полагаем
. Полагаем  . Тогда
. Тогда  и, значит, по формуле (3.2*).
и, значит, по формуле (3.2*).  .
.
2.  .
.
3. 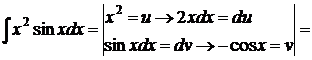
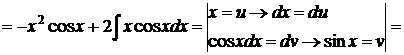
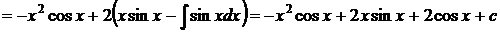
Формулу интегрирования по частям применили дважды.
4. 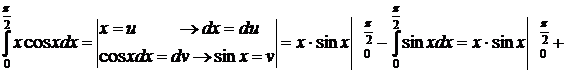
 .
.
 называется первообразнойфункцией для функции
называется первообразнойфункцией для функции 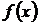 на промежутке
на промежутке 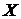 , если в каждой точке
, если в каждой точке 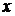 этого промежутке
этого промежутке  .
. 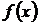 на промежутке
на промежутке 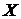 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 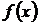 и обозначается
и обозначается  . Таким образом:
. Таким образом:  , где
, где  - некоторая первообразная для
- некоторая первообразная для 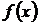 , с – произвольная постоянная.
, с – произвольная постоянная.  .
. .
. .
. .
. , где
, где - некоторое число.
- некоторое число. .
. .
. ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.  - первообразная функция от
- первообразная функция от 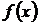 , т.е.
, т.е.  , то
, то  .
.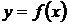 непрерывна на отрезке
непрерывна на отрезке  и внутри этого отрезка всюду неотрицательна, то определенный интеграл
и внутри этого отрезка всюду неотрицательна, то определенный интеграл  представляет собой в декартовой системе координат площадь криволинейной трапеции
представляет собой в декартовой системе координат площадь криволинейной трапеции  (см. рис. 12), ограниченной графиком подинтегральной функции
(см. рис. 12), ограниченной графиком подинтегральной функции 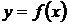 , осью
, осью  и двумя прямыми
и двумя прямыми  .
.
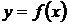



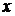
 ;
; ;
; ;
; ;
; постоянная, то
постоянная, то  ;
; .
.
 .
.
 .
.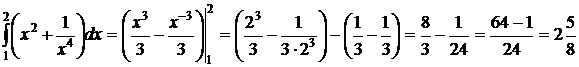
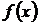 , где
, где  , тогда:
, тогда: (3.1)
(3.1) надо вместо
надо вместо  подставить его выражение через
подставить его выражение через 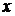 . В определенном интеграле возврат к переменной
. В определенном интеграле возврат к переменной 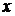 не обязателен, но в этом случае при замене переменной необходимо изменить пределы интегрирования, т. е. воспользоваться формулой:
не обязателен, но в этом случае при замене переменной необходимо изменить пределы интегрирования, т. е. воспользоваться формулой: .
. .
. , тогда
, тогда  и, следовательно,
и, следовательно,  .
. .
. .
. .
. . Дифференцируя это соотношение, находим
. Дифференцируя это соотношение, находим 
 , откуда
, откуда  . Находим теперь новые пределы интеграла. Для этого из соотношения
. Находим теперь новые пределы интеграла. Для этого из соотношения  определяем
определяем  при
при  и
и  при
при  . Итак, имеем
. Итак, имеем 
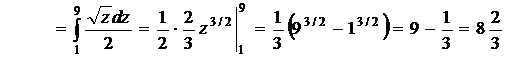
 и
и  непрерывно дифференцируемы на некотором промежутке, тогда:
непрерывно дифференцируемы на некотором промежутке, тогда: . (3.2)
. (3.2) . (3.2*)
. (3.2*) .
.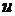 и
и  они сводят нахождение интеграла от
они сводят нахождение интеграла от  после частичного интегрирования к нахождению интеграла от
после частичного интегрирования к нахождению интеграла от  . Иногда удается функции
. Иногда удается функции 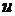 и
и  выбрать так, что новый интеграл либо сам является табличным, либо сводится к табличным интегралам уже известными методами.
выбрать так, что новый интеграл либо сам является табличным, либо сводится к табличным интегралам уже известными методами.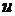 принимается функция, которая дифференцированием упрощается, а за
принимается функция, которая дифференцированием упрощается, а за  - та часть подынтегрального выражения, содержащая
- та часть подынтегрального выражения, содержащая  , интеграл от которой известен или может быть найден.
, интеграл от которой известен или может быть найден. ,
,  ,
,  за
за 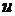 следует принять многочлен
следует принять многочлен  , а за
, а за  - соответственно выражения -
- соответственно выражения -  ,
,  ,
,  .
. ,
,  ,
,  за
за  следует принять выражение
следует принять выражение  , а за
, а за 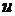 - соответственно функции
- соответственно функции  ,
,  ,
,  .
. . Полагаем
. Полагаем  . Тогда
. Тогда  и, значит, по формуле (3.2*).
и, значит, по формуле (3.2*).  .
. .
.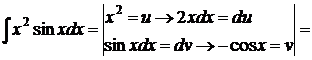
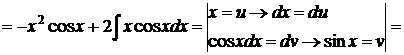
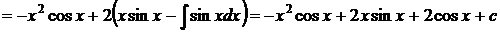
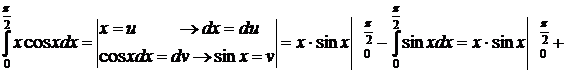
 .
.