Получите формулу для потенциальной энергии тела в гравитационном поле Земли (вдали от поверхности Земли).

Потенциальная энергия (или энергия положения тел) определяется действием на тело консервативных сил и зависит только от положения тела.

Мы видели, что работу силы тяжести 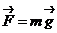при криволинейном движении материальной точки 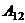можно представить в виде разности значений функции 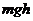, взятых в точке 1 и в точке 2: .

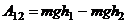Оказывается, что всегда, когда силы консервативны, работу этих сил на пути 1 2 можно представить в виде:

.

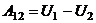Функция 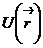, которая зависит только от положения тела – называется потенциальной энергией.

36. Какие законы сохранения выполняются при движении тела в центральном гра­витационном поле? Получите явные выражения для этих законов сохранения. Какие следствия вытекают из этих законов сохранения?

37. Получите формулы для первой и второй космических скоростей тела, движуще­гося в I рант анионном поле Земли.

Это задача небесной механики.

Рассмотрим гравитационное поле Солнца.

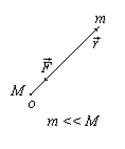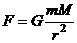- закон всемирного тяготения,

где G = 6.67 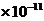Нм²/кг² -

- гравитационная постоянная.

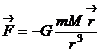-сила гравитационного притяжения.

Гравитационное взаимодействие осуществляется через гравитационное поле.

1) Гравитационная сила – консервативная сила

,

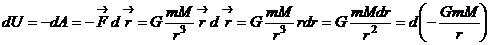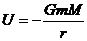-потенциальная энергия гравитационного поля.

Имеет место закон сохранения механической энергии тела.

E = W + U = const - закон сохранения энергии тела.

2) Гравитационная сила – центральная сила:

Возьмем момент импульса 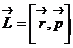и рассмотрим закон изменения его во времени:

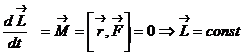-- закон сохранениямомента импульса тела.

Поскольку момент импульса тела сохраняется, движение тела происходит в одной плоскости.Приступим теперь к рассмотрению движения тела: .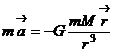

Удобно перейти к системе отсчета, которая связана с 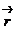и вращается с угловой скоростью 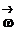. ( 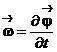- угловая скорость)

Во вращающейся системе отсчета надо добавить центробежную силу, поэтому уравнение (1) примет вид:

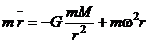уравнение движения во вращающейся системе отсчета.

Вычислим :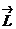

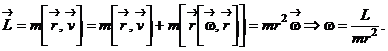
Здесь использована формула раскрытия двойного векторного произведения

.

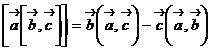Тогда (2) примет вид: 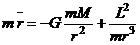. (3)

Перейдем к полярной системе координат и выразим r как функцию угла 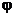, т.е. 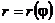. Можно показать, что решение уравнения (3) может быть представлено следующим образом: 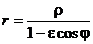траектория движения тела в полярных координатах,

где 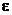- эксцентриситет, 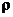- параметр, определяющий размеры траектории.

Возможны 4 типа траекторий:

1) 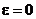- окружность;

2) 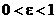- эллипс;

3) 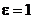- парабола;

4) 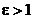- гипербола.

Рассмотрим качественно характер движения с помощью потенциальной кривой. Для этого введем потенциальную энергию центробежной силы:

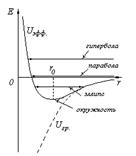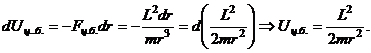
Тогда во вращающейся системе отсчета:

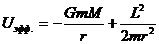- эффективная потенциальная энергия.

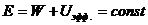- закон сохранения энергии.

Посмотрим, от каких физических величин зависит эксцентриситет орбиты 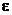и параметр 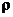. Вернемся к неподвижной системе отсчета.

,

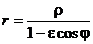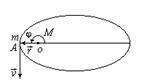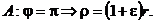(5)

Используем законы сохранения энергии и момента импульса.

Для точки А:

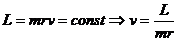
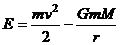= const.

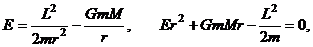
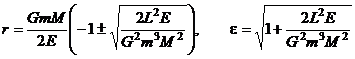– (6)

– эксцентриситет орбиты.

--малая и большая полуоси.

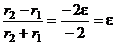- действительно эксцентриситет эллипса.

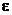Подставляя и 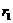в (5), получим

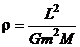- параметр орбиты. (7)

Из формулы (6) получим энергию E:

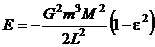- полная механическая энергия тела.

Введем в точке A ускорение свободного падения g: .

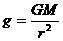Тогда ,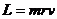

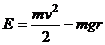
Подставляя L и E в (6) и (7), получим

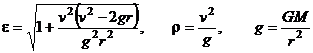- ускорение свободного падения в точке A.

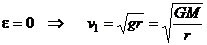- первая космическая скорость,

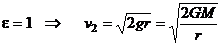- вторая космическая скорость.