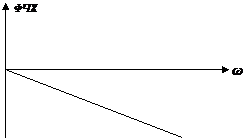
Для неискажающей цепи АЧХ должна быть постоянной на всех частотах, а ФЧХ должна быть линейной функцией от частоты.
Если АЧХ – постоянная, то соотношение между амплитудами спектральных составляющих остается неизменным. Если время запаздывания t3 для всех составляющих одинаково, то они одинаково запаздывают т.к. t3 является производной от ФЧХ, а для линейной оно постоянно.
Графически это можно изобразить следующим образом:
Практически таких характеристик не бывает. Реально нет цепей без искажения сигнала, можно передавать сигналы с некоторыми минимальными искажениями.
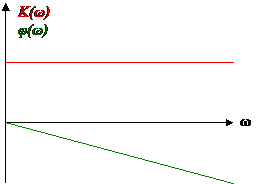
Третье требование – не должно быть отражения сигнала или «эха».
Спектральный или частотный метод расчета в ТЦ

Фактически выделяют четыре этапа:
1) Находится спектральная плотность на входе;
2) Находится комплексный коэффициент передачи;
Находится спектральная плотность на выходе.
Находится сигнал на выходе.
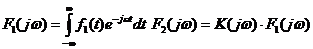
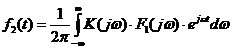
Прохождение сигналов через RL-цепочки
Рассмотрим прохождение сигнала δ - функции через RL – цепочку .
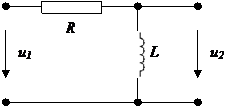 сх.1
сх.1 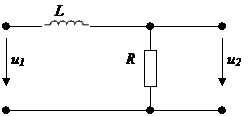 сх.2
сх.2
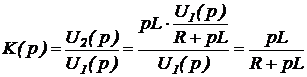 Аналогично можно и для 2 схемы
Аналогично можно и для 2 схемы
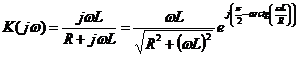
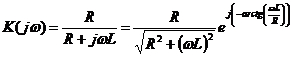
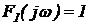 (типовой сигнал).
(типовой сигнал). 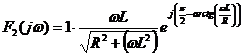
Проведем качественный анализ.
Если сильно уменьшаются низкочастотные составляющие (влияющие на медленные участки), то будут сильно меняться на выходе плоские участки сигнала (вершины сигнала). Это характерно для 1 схемы (RL).
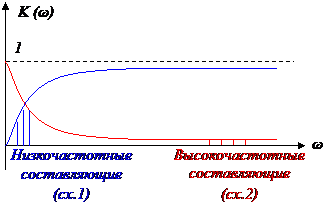 Высокочастотные составляющие – быстрые составляющие, характеризующие участки быстрого изменения сигнала (фронта сигнала). Если сильно уменьшаются высокочастотные составляющие, то будут сильно изменяться резкие, быстрые участки сигнала (фронты). Это характерно для 2 схемы (LR).
Высокочастотные составляющие – быстрые составляющие, характеризующие участки быстрого изменения сигнала (фронта сигнала). Если сильно уменьшаются высокочастотные составляющие, то будут сильно изменяться резкие, быстрые участки сигнала (фронты). Это характерно для 2 схемы (LR).
Частотный анализ ЛЭЦ при непериодических воздействиях
Для определения выходной реакции линейной электрической цепи используют комплексную передаточную функцию 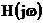 . При этом спектр выходной реакции определяется в виде:
. При этом спектр выходной реакции определяется в виде: 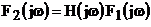 . Рассчитаем комплексную спектральную плотность
. Рассчитаем комплексную спектральную плотность
| |
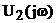 в
в 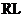 – цепи, если на ее вход действует сигнал в форме прямоугольного импульса. Комплексная передаточная функция определяется как:
– цепи, если на ее вход действует сигнал в форме прямоугольного импульса. Комплексная передаточная функция определяется как: 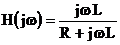 . Здесь будут ослабляться на выходе низкочастотные составляющие.
. Здесь будут ослабляться на выходе низкочастотные составляющие.
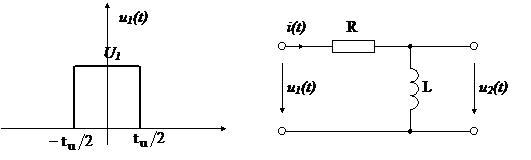
Спектральная плотность прямоугольного импульса: 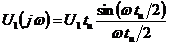 .
.
Комплексная спектральная плотность сигнала на выходе:
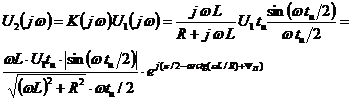 .
.
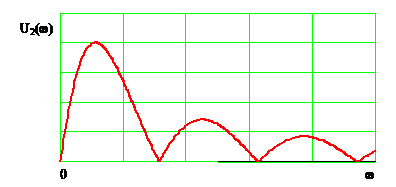 Определим амплитудный спектр выходного напряжения
Определим амплитудный спектр выходного напряжения 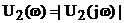 .Для этого надо перемножить значения АЧХ на значения АЧС входного сигнала.
.Для этого надо перемножить значения АЧХ на значения АЧС входного сигнала.
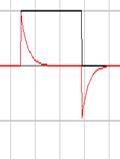
Спектр выходного сигнала Форма выходного сигнала
Прохождение импульсных сигналов через цепь с ограниченной полосой пропускания
Под полосой пропускания понимают частотный диапазон характеристики цепи, где значение АЧХ не сильно меняется ( 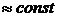 ). Рассмотрим цепь с характеристиками
). Рассмотрим цепь с характеристиками
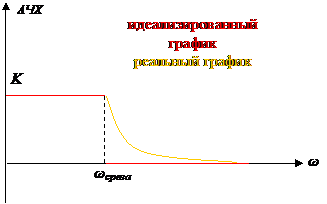
| |
| |
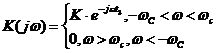
1) Сигнал δ(t) – единичная импульсная функция

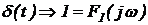
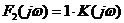
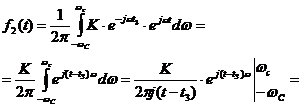
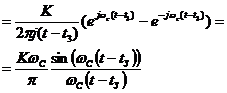
Получим
сигнал с высотой 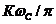 . Видно, что сигнал исказился, он не является δ функцией. Нулевые точки в выходном сигнале будут определяться из соотношений
. Видно, что сигнал исказился, он не является δ функцией. Нулевые точки в выходном сигнале будут определяться из соотношений 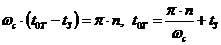 При ωС→∞ получим на выходе бесконечно большую амплитуду (повторение входного сигнала, но с запаздыванием и с 0 расстоянием между нулевыми точками то есть δ функцию).
При ωС→∞ получим на выходе бесконечно большую амплитуду (повторение входного сигнала, но с запаздыванием и с 0 расстоянием между нулевыми точками то есть δ функцию).
2) σ(t) – единичная ступенчатая функция(скачок)

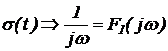
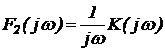
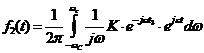
Результат такого интегрирования называют интегральным синусом 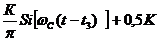 с расстоянием по времени между нулем функции
с расстоянием по времени между нулем функции
ближайшим 0,5K и уровнем К
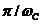 (крутизной
(крутизной 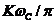 ). То есть сигнал не соответствует исходному, он исказился.
). То есть сигнал не соответствует исходному, он исказился.
При ωС→∞ получим на выходе бесконечно большую крутизну сигнала (скачок, но запаздывающий).
3) Прямоугольный импульс
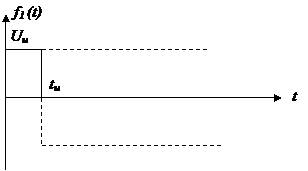 Необходимо разбить сигнал на две ступенчатые функции: положительную и отрицательную.
Необходимо разбить сигнал на две ступенчатые функции: положительную и отрицательную.

| |
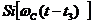 и ─ интегральный синус с запаздыванием tЗ+tu
и ─ интегральный синус с запаздыванием tЗ+tu - 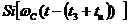 .
.
Если 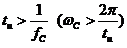 , то импульс считается длинный, основная часть спектра импульса попадает в полосу пропускания и проходит на выход цепи. Переходные процессы за время импульса успевают практически закончиться. В итоге импульс не сильно искажается.
, то импульс считается длинный, основная часть спектра импульса попадает в полосу пропускания и проходит на выход цепи. Переходные процессы за время импульса успевают практически закончиться. В итоге импульс не сильно искажается.
Если ωС→∞, то сигнал на выходе повторит входной импульс с множителем К, но с запаздыванием.
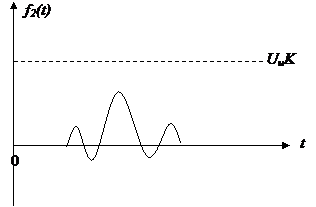
Если 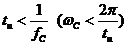 , то основная часть спектра импульса не попадает в полосу пропускания (импульс короткий), и не проходит на выход цепи. Переходные процессы за время импульса не успевают закончиться. В итоге импульс сильно искажается.
, то основная часть спектра импульса не попадает в полосу пропускания (импульс короткий), и не проходит на выход цепи. Переходные процессы за время импульса не успевают закончиться. В итоге импульс сильно искажается.
