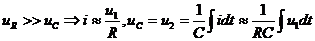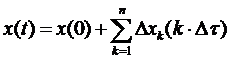Экспериментально - не получится.
Пример нахождения временных характеристик
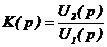
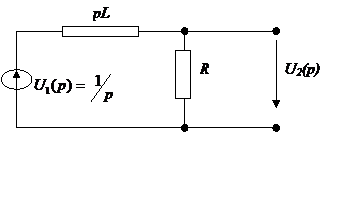
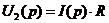
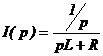
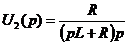
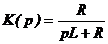
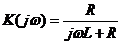
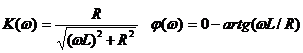
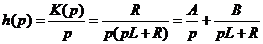
Определив коэффициенты A и B, получаем: 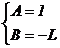
Тогда: 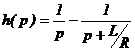
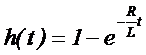
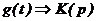
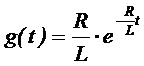
ω=2πf
Расчет откликов в электрической цепи на кусочно-непрерывное воздействие.
(Интеграллы Дюамеля и наложения)
При передаче информации сигналы могут быть сложными функциями, состоящими из отдельных скачкообразных воздействий.
 |
В каждом интервале функция меняется по одному закону.
Разобьем функцию воздействия на элементарные ступеньки
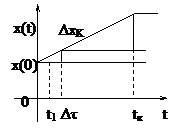 | |||
| |||
Δτ→0 Δx=x/ Δτ
Y(t) определяется с помощью переходной характеристики
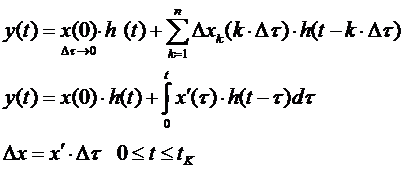 Это и есть интеграл Дюамеля
Это и есть интеграл Дюамеля
Интеграл наложения основан на разбиении функции воздействия на элементарные импульсы
Реакцию на импульсное воздействие можно найти с помощью импульсной характеристики с учетом площади импульса 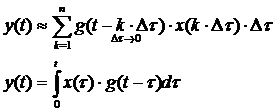

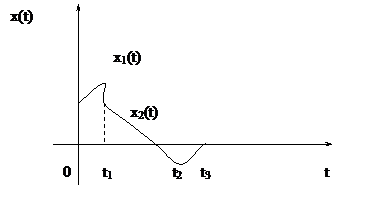

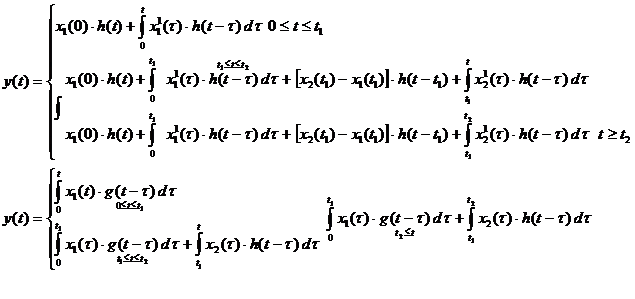
Определение отклика на прямоугольный импульс.
Классический метод
 Можно рассчитывать отдельно на включение импульса и на выключение, если за время импульса переходный процесс закончится.
Можно рассчитывать отдельно на включение импульса и на выключение, если за время импульса переходный процесс закончится.
Операторный метод
 |

Находим X(p)=(по Лапласу)
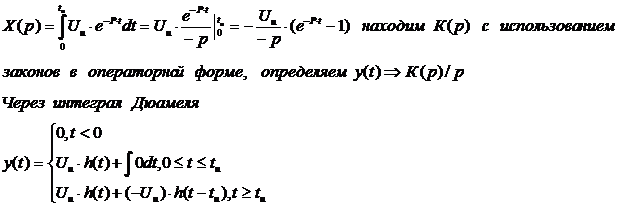
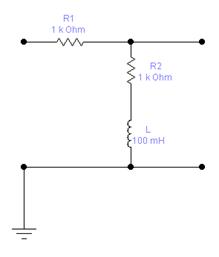 Возьмем для примера цепь:
Возьмем для примера цепь:
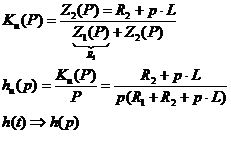
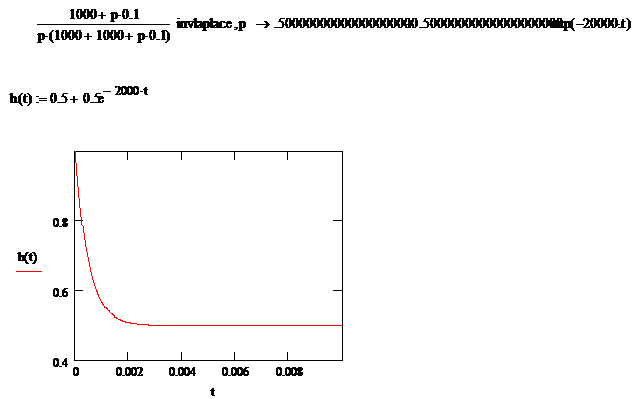
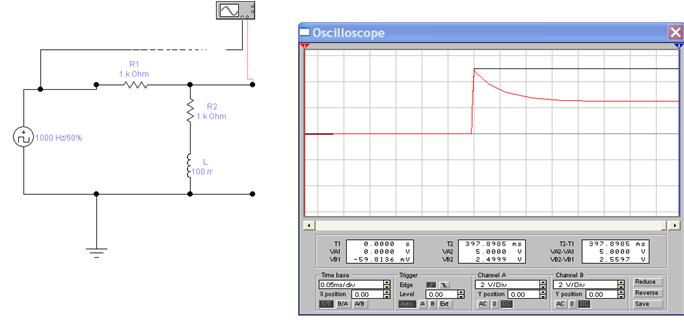
Дифференцирующие и интегрирующие цепи
Общие понятия
При обработке электрических сигналов может возникнуть задача дифференцирования или интегрирования сигнала, т.е. чтобы реакция на выходе цепи была пропорциональна производной или интегралу входного сигнала.
Дифференцирующими и интегрирующими называют цепи, которые имеют на выходе напряжение, пропорциональное производной или интегралу от входного напряжения.
Дифференцирующие цепи

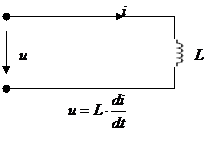
Это простейшие дифференцирующие цепи.
Однако, часто требуется, чтобы именно напряжение на выходе было пропорционально производной напряжения на входе.
Тогда можно составить такую цепь:
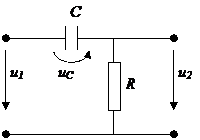
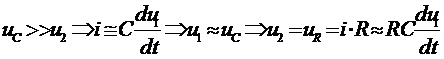
Здесь дифференцирование будет приблизительным.
Чем лучше выполняется соотношение 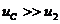 , тем точнее дифференцирование, но при этом меньше напряжение на выходе. Сопротивление R и емкость С должно быть небольшими. В итоге постоянная времени τцепи должна быть маленькой. Значит, цепь быстро реагирует на все изменения, успевает следить за изменением входного сигнала, что и нужно, поскольку производная оценивает скорость изменения сигнала.
, тем точнее дифференцирование, но при этом меньше напряжение на выходе. Сопротивление R и емкость С должно быть небольшими. В итоге постоянная времени τцепи должна быть маленькой. Значит, цепь быстро реагирует на все изменения, успевает следить за изменением входного сигнала, что и нужно, поскольку производная оценивает скорость изменения сигнала.
Аналогично RL-цепь.
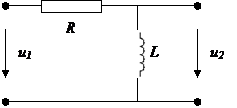
В данном случае должны выполняться условия: 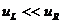 , сопротивление должно быть большим, а индуктивность малой. В итоге постоянная времени малая.
, сопротивление должно быть большим, а индуктивность малой. В итоге постоянная времени малая.
На практике большее применение получила RC-цепь, так как сам конденсатор – элемент с меньшими потерями.
Используют и такие цепи

С точки зрения ТЦ операционный усилитель (ОУ) – это ИНУН, у которого коэффициент усиления 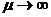 .
.
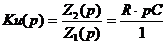
Умножение на p говорит о дифференцировании. Следовательно, это дифференцирующая цепь. Здесь на выходе будет достаточно большое напряжение.
С индуктивностью такая цепь не применяется.
Применение: определение начала и конца прямоугольного сигнала (в телевидении: начало и конец строки); можно применять в аналоговых ЭВМ.
Интегрирующие цепи
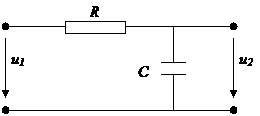 Условия:
Условия: