Теоремы об эквивалентных источниках или генераторах

(Теорема об автономном двухполюснике)

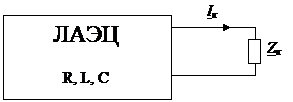
ЛАЭЦ – линейная активная электрическая цепь, содержит линейные

RLC-элементы, источники тока и напряжения с одной и той же частотой.

Теорема 1 (об эквивалентном источнике напряжения): Ток в некоторой ветви, подключенной к ЛАЭЦ, не изменится, если эту ЛАЭЦ заменить эквивалентным источником напряжения, содержащим идеальный источник напряжения с ЭДС, равной напряжению холостого хода активной цепи, и эквивалентное сопротивление, последовательно включенное, равное входному (выходному) сопротивлению пассивизированной активной цепи.

ZЭИ

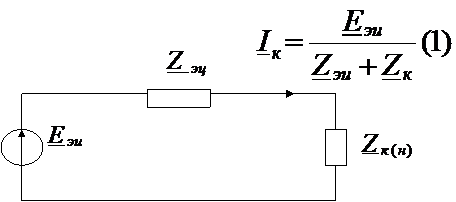
Доказательство: Вставим в выделенную ветвь два одинаковых источника напряжения Е_Х, но противоположных направлений. Ток при этом не изменится.

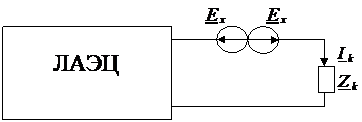
По принципу наложения можно записать:

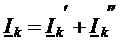, где 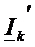- ток только под действием 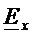того же направления( ),

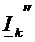- под действием 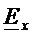противоположного направления ( ) и источников внутри ЛАЭЦ.

1)в первом случае получим вместо активной цепи пассивизированную цепь (без внутренних источников):

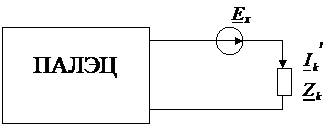
Можем найти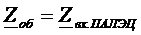

2) Поставим задачу, чтобы .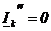

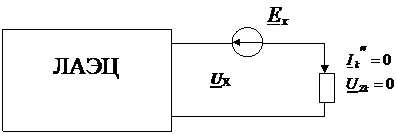
Мы получили не что иное, как режим холостого хода, где U_Zk=0, и U_X=E_X=U_XX.

Итак, мы доказали, что .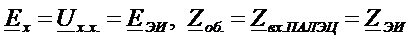

У нас .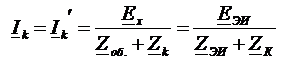

Теорема 2 (об эквивалентном источнике тока): Ток в некоторой ветви, подключенной к ЛАЭЦ, не изменится, если ЛАЭЦ заменить эквивалентным источником тока, содержащим идеальный источник тока, и параллельно подключенное сопротивление или проводимость; ток идеального источника равен току короткого замыкания ЛАЭЦ; проводимость эквивалентного источника равна входной проводимости пассивизированной ЛАЭЦ.

Как видно это дуальная теорема.

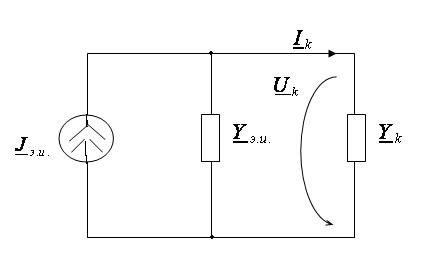
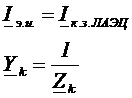
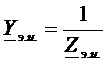
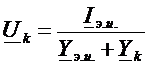
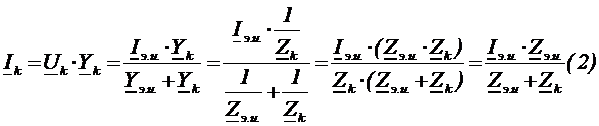
Метод эквивалентного источника напряжения или тока

Применяется по соответствующей теореме, когда надо рассчитать один ток в какой-то одной ветви.

1) Для нахождения ЭДС размыкают ветвь с неизвестным током и находят напряжение 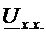, применяя законы Ома, Кирхгофа и т.д., либо накоротко замыкают и рассчитывают ток короткого замыкания.

2) Для нахождения 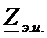размыкают ветвь и находят 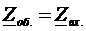, заменяя в ЛАЭЦ идеальные источники напряжения – перемычками, источники тока – разрывом.

3) Находят 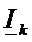(или по формуле (1), или по формуле (2)), при расчете учитывается, что 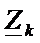имеет смысл нагрузочного сопротивления, которое может меняться, а 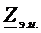и 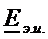параметры активной цепи, которые не меняются с изменением нагрузки.

Теорема обратимости или взаимности

Справедлива для линейных обратимых цепей:, где все элементы линейны и обратимы по передаче электрической энергии (движения зарядов) в одну и другую сторону.

Теорема Если некоторый источник ЭДС вызывает в какой-то ветви пассивной обратимой цепи некоторый ток, то будучи перемещен в эту вторую ветвь, он вызовет в первой ветви, где раньше был, точно такой же ток. Справедлива и дуальная теорема.

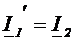
Доказательство

Применим метод контурных токов, будем выбирать контуры так, чтобы первая ветвь входила только в один первый контур, а вторая – только во второй контур, тогда токи этих ветвей будут равны этим контурным токам.

В первой схеме:

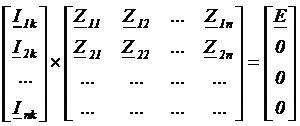Здесь Z_11,22…nn.-контурные сопротивления, Z_12,13,….ki – взаимные сопротивления контуров.

Во второй :

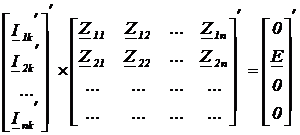, тогда

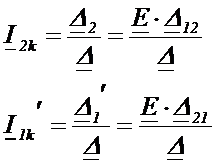
Эти два выражения отличаются на 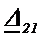и 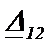. Если все элементы в цепи обратимы, то 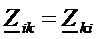. В этом случае 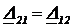и .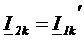

Применение теоремы

Теорему целесообразно применять при расчете токов методом наложения, когда надо находить частичные токи от каждого источника в отдельности, рассчитав ток от одного источника напряжения и пропорционально изменяя токи от источников в других ветвях.

Примеры