Источники неоднородностей. Понятие дрейфа и качественного фактора

Планирование эксперимента в условиях дискретного дрейфа

Планирование в условиях линейного непрерывного дрейфа

ИСТОЧНИКИ НЕОДНОРОДНОСТЕЙ.
ПОНЯТИЕ ДРЕЙФА И КАЧЕСТВЕННОГО ФАКТОРА

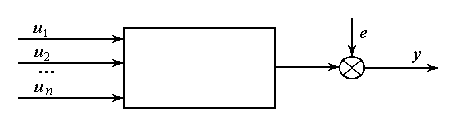
Представление объекта исследования традиционной схемой не всегда возможно. Часто кроме управляемых входных переменных на вход влияют так называемые источники неоднородностей, т.е. некоторые воздействия, искажающие результаты эксперимента при стабильных значениях факторов планирования. При этом в отличие от шума е(t), эти источники оказывают детерминирующее воздействие на объект.

К числу источников неоднородностей относятся:

- неуправляемый дрейф;

- качественные факторы.

Дрейф - детерминированное изменение выхода объекта при стабильных значениях факторов планирования U.

Дрейф может быть дискретным и непрерывным.

Источником дискретного дрейфа могут быть колебания качества сырья, неодинаковая квалификация исследователей, различная точность приборов и т.п.

Источники непрерывного дрейфа - колебания качества сырья катализатора в химических процессах, старение аппаратуры и пр. Непрерывный дрейф может быть как линейным, так и нелинейным.

Качественные факторы - такие управляющие воздействия, которые не могут быть охарактеризованы количественно. Примерами качественных факторов являются: тип проволоки в сварочном аппарате, добавки при легировании стали и т.п.

Возможны две постановки задачи планирования эксперимента при наличии источников неоднородностей.

Подход 1.

Необходимо так спланировать эксперимент, чтобы получить модель, связывающую выход объекта с количественными факторами планирования независимо от действия источников неоднородности.

Это возможно только при первом типе источников неоднородностей. Другими словами, этот подход называется планированием ортогонально дрейфу.

Подход II .

Данный подход заключается в построении модели, учитывающей не только количественные факторы, но и источники неоднородностей.

Планирование эксперимента
в условиях дискретного дрейфа

Предположим, что надо исследовать влияние трех количественных факторов при необходимости проведения всех опытов в две серии:

n=3; число опытов - 2^3.

Нужно получить линейную модель:

Для разбиения ПФЭ на две серии используется следующий прием: в качестве первого блока используется полуреплика с генерирующим соотношением , а в качестве второго блока - полуреплика с генерирующим соотношением .

Каждый из полученных блоков полностью ортогонален, т.е. все столбцы полностью ортогональны. Поскольку в первом блоке тройное взаимодействие равно +1, а во втором -1 , то это взаимодействие можно принять в качестве дополнительного фактора, который будем называть межблоковым дрейфом и обозначать .

Покажем, что при таком планировании оценки неизвестных коэффициентов модели не зависят от дрейфа. Обозначим результаты первого блока соответственно, результаты второго блока - , где - систематическое смещение выхода, вызванное изменением условий проведения эксперимента.

Найдем оценку коэффициентов:

Аналогично можно показать, что оценки всех остальных коэффициентов модели не зависят от дрейфа как и коэффициент .

Оценим коэффициент при дрейфе :

Если необходимо исследовать влияние четырех факторов и необходимо провести опыты в две серии, то блоки будут следующие:

I блок - полуреплика 2^4-1; ГС:

II блок - полуреплика 2^4-1; ГС:

Если необходимо разбить план на четыре блока:

I блок 1/4 реплики 2^4-2; ГС:

II блок 1/4 реплики 2^4-2; ГС:

III c блок 1/4 реплики 2^4-2; ГС:

IV блок 1/4 реплики 2^4-2; ГС:

Планирование в условиях линейного непрерывного дрейфа.

Данное планирование используется тогда, когда при стабильном входе происходит изменение выхода на одну и ту же величину.

В этом случае можно построить регрессионную модель, связывающую вход с количественными факторами планирования и описывающую дрейф. Предварительно нужно убедиться, что дрейф линейный.

Если объект подвержен линейному дрейфу, то опыты нужно проводить через одно и то же время: , где - время переходного процесса по i-ому каналу.

Для построения модели, ортогональной линейному дрейфу можно использовать планы типа ПФЭ, если выполняется следующее условие:

При этом первые L+1 столбцов матрицы базисных функций F используются для представления линейного дрейфа. Остальные столбцы матрицы F используются для планирования и задания парных взаимодействий.

Рассмотрим пример.

Необходимо построить модель вида при наличии линейного дрейфа. При этом

Модель дрейфа запишем в виде:

Запишем матрицу базисных функций:

После реализации плана u₁, u₂ на объекте через одинаковые интервалы времени и определения значений выхода необходимо вычислить МНК-оценки всех неизвестных коэффициентов модели: . В результате получается модель вида:

Если дрейф нелинейный, то можно использовать ту же методику планирования, если опыты проводить через неодинаковые интервалы времени при условии, что за время между двумя соседними опытами дрейф имеет одинаковые значения.

Тема 18. Планирование эксперимента при наличии количественных и качественных факторов

18.1. Постановка задачи планирования эксперимента при наличии качественных факторов

18.2. Решение задач планирования с использованием совмещенных планов

18.3. Примеры совмещенных планов