Определение структуры модели Вольтерра. Способы представления ядер

8.4.2. Построение модели Вольтерра при известном значении параметра α

8.4.3. Построение модели Вольтерра при неизвестном значении параметра α

Нелинейные объекты управления делятся на два класса:
1. нелинейные объекты управления, допускающие каскадное представление;
2. нелинейные объекты управления, не допускающие каскадное представление.
Первый класс моделей можно описать моделями Винера-Гаммерштейна, а второй класс моделями Вольтерра.

МОДЕЛЬ ВИНЕРА

Модель Винера - последовательное соединение линейной инерционной части и нелинейной безынерционной части.

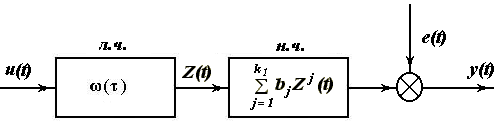
Линейную часть будем описывать в виде импульсной переходной функции.
Модель нелинейной части описывается в виде отрезка степенного ряда: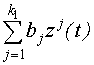

Неизвестные параметры модели Винера: .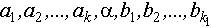

Кроме этих параметров в число неизвестных параметров модели Винера необходимо включить постоянную составляющую выходного сигнала:

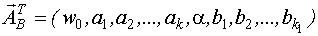
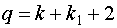- число неизвестных параметров в модели Винера.

Необходимость введения в модель постоянной составляющей вызвана невыполнением принципа суперпозиции для нелинейных систем.

Таким образом, нелинейная система должна связывать истинные значения выхода и входа.

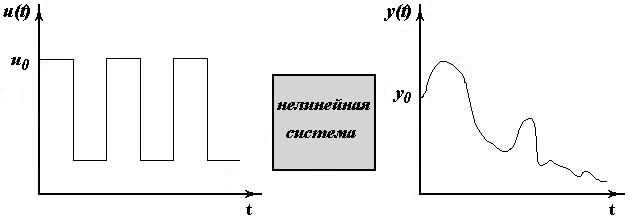
После представления линейной и нелинейной частей каскадной модели необходимо определить структуру соответствующей динамической регрессионной модели, в данном случае - модели Винера.

Получим структуру этой модели в предположении, что входной сигнал является кусочно-постоянной функцией времени:

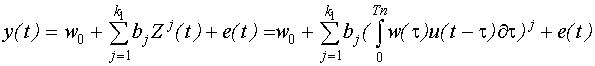
Если запишем в виде 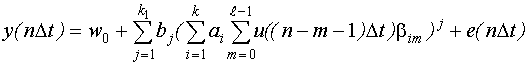, то получим линейно-комбинационную модель Винера.

Полученная модель существенно нелинейна по всем неизвестным параметрам, кроме постоянной составляющей выходного сигнала, поэтому оценивание неизвестных параметров этой модели возможно только нелинейными методами.

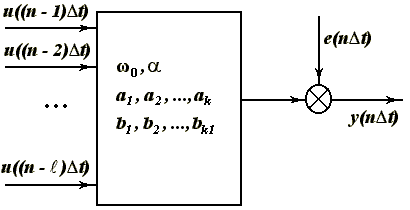
Оценивание вектора неизвестных параметров производится по тем же формулам что и для линейного объекта при подстановке в них вектора-функции частных производных

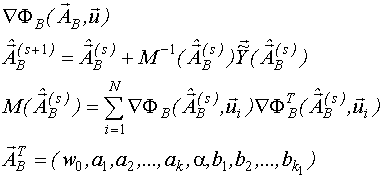
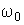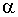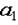Берем производную по , потом по , по и так далее.

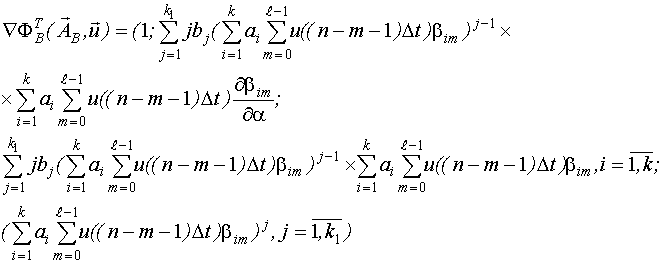
Начальное приближение вектора неизвестных параметров 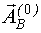, в отличиe от начального приближения вектора неизвестных параметров 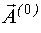, оценить достаточно сложно. Обычно приближение задается произвольно, что усложняет процедуру.

МОДЕЛЬ ГАММЕРШТЕЙНА

Модель Гаммерштейна - последовательное соединение нелинейной безинерционной части и линейной инерционной части.

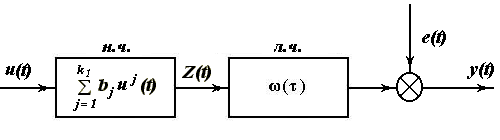
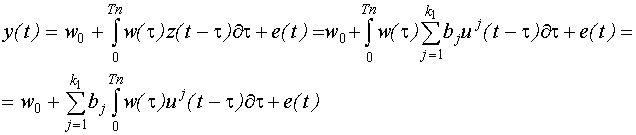
Получим выражение для случая кусочно-постоянного входного сигнала в дискретной форме.

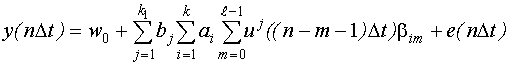
Модель Гаммерштейна содержит те же параметры что и модель Винера, но структура модели другая. Она линейна только 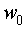по , по .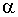

Получим выражение для вектора функции 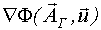, причем .

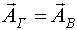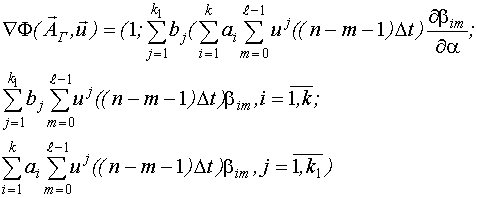
МОДЕЛЬ ВИНЕРА-ГАММЕРШТЕЙНА

Модель Винера-Гаммерштейна - последовательное соединение двух линейных инерционных частей разделенных одной нелинейной безинерционной частью.

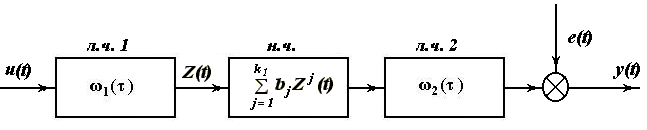
МОДЕЛЬ ВОЛЬТЕРРА
Определение структуры модели Вольтерра. Способы представления ядер.

Определение структуры модели Вольтерра. Способы представления ядер.
Модели Вольтерра - наиболее общий класс моделей нелинейных систем, частным случаем моделей Вольтера являются модели Винера и Винера-Гаммерштейна.
Модель Вольтерра - модель основанная на функционально-степенном ряду Вольтерра. В частности, модель Вольтерра является трехчленным отрезком ряда Вольтерра.
Ряд Вольтерра имеет вид:

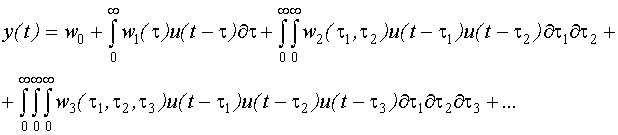
В общем виде:

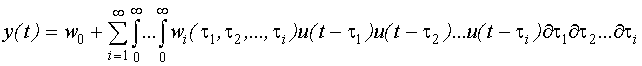
В задачах идентификации используется трехчленный отрезок ряда Вольтерра, то есть выражение вида:
,
где 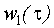- ядро Вольтерра первого порядка;
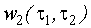- ядро Вольтерра второго порядка;
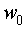- ядро Вольтерра нулевого порядка или постоянная составляющая.

Обычно ядра представлены в виде разложения по базисным функциям (чаще всего используются функции Лагерра). Представление ядер в виде ординат импульсной переходной функции обычно не используется, так как ему соответствует слишком большой вектор неизвестных параметров.
Будем представлять ядро первого порядка:

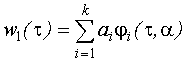
Ядро второго порядка:

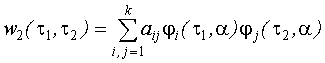
Это сепарабельное представление, то есть функция двух аргументов представлена в виде произведения двух функций одного аргумента.

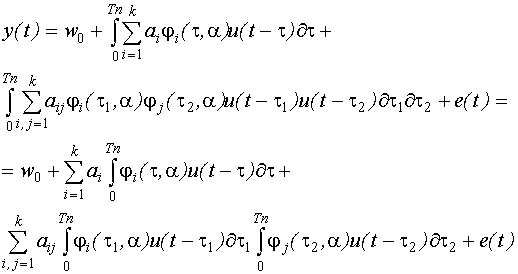
Получим дискретную регрессионную модель Вольтерра вида:

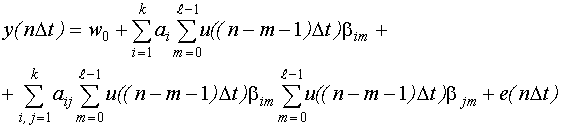
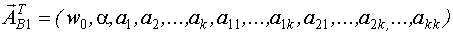
Вектор неизвестных параметров:

- число неизвестных параметров.

Данная модель нелинейно-параметризованная, но если известен параметр 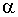, то модель линейно-параметризованная, следовательно, возможны два метода вычисления оценок вектора неизвестных параметров:

1- метод наименьших квадратов, если параметр 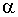определен из оценки времени переходного процесса;

2- метод, основанный на нелинейном оценивании вектора неизвестных параметров.

Построение модели Вольтерра при известном значении параметра .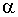

Метод построения модели Вольтерра при известном значении параметра 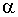основан на оценивании вектора .

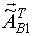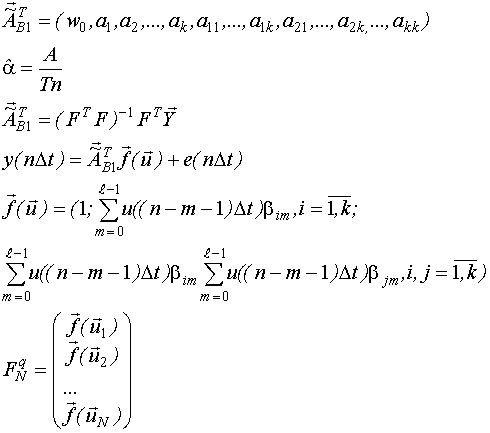
Построение модели Вольтерра при неизвестном значении параметра .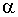

Построение модели Вольтерра при неизвестном значении параметра 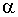предполагает оценивание всего вектора неизвестных параметров

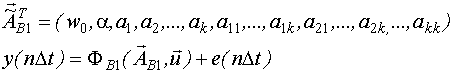
В качестве начального приближения вектора неизвестных параметров используют следующий вектор:

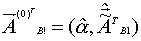
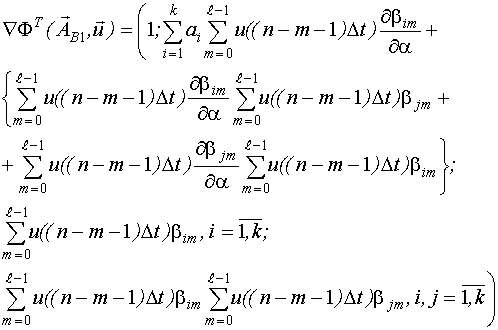
Модель Вольтерра - это обобщенная модель нелинейной системы, частным случаем которой является модель Винера.
Покажем, что при 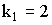модель Винера является частным случаем трехчленного отрезка ряда Вольтерра:

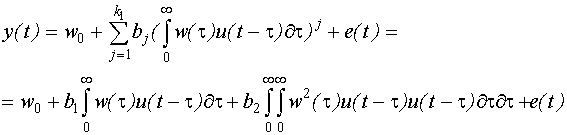
Если 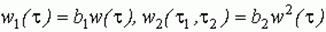, то модель Винера совпадает с моделью Вольтерра.
Модель Винера-Гаммерштейна так же является частным случаем модели Вольтерра.