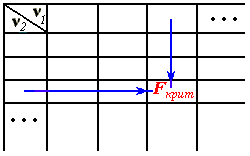
OМНК при большом объеме выборки

Известно, что в асимптотике (при 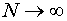) Марковские оценки стремятся к МНК оценкам, но ковариационная матрица этих оценок вычисляется по другим выражениям.

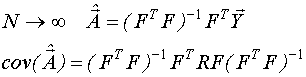
Если обращение не коррелированно, то .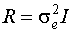

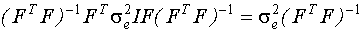
Таким образом, при большом объеме выборки (число измерений больше 100) вместо Марковских оценок можно использовать МНК оценки с преобразованной ковариационной матрицей. Это значительно проще с вычислительной точки зрения.

Метод максимального правдоподобия

Идея метода заключается в следующем. Имеется объект с n входами.

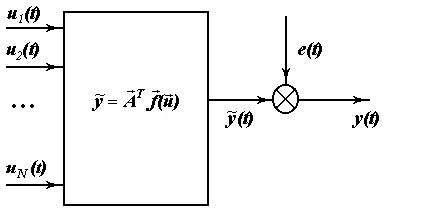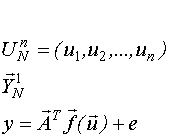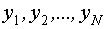- случайные величины, имеющие какое-то распределение.
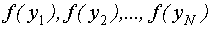- плотность распределения.

Поскольку источником распределения случайных величин 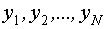является наличие случайной величины e(t), то законы распределения 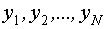совпадают с законом распределения e(t).

Параметры распределения разные, причем математическое ожидание разное, а дисперсии при стационарном случайном процессе e(t) одинаковы.

Зная плотности распределения, можно вычислить функцию правдоподобия:

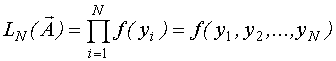
В частном случае, если измерения независимы, n-мерная плотность распределения равна произведению .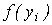

Функция правдоподобия зависит от известных параметров.

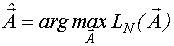- это оценка максимального правдоподобия.

Оценка максимального правдоподобия максимизирует нашу функцию.

Для упрощения вычислений обычно максимизируют не исходную функцию правдоподобия, а логарифмическую функцию правдоподобия:

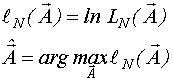
Рассмотрим пример.
Есть модель y=au+e, измерения входа 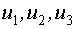, измерения выхода .
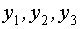Найти .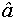

Предположим, что закон распределения случайной величины нормальный: .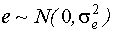

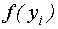-нормально - распределенная величина.

Найдем 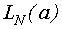. 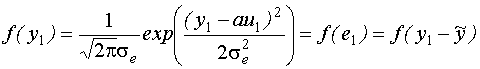, так как

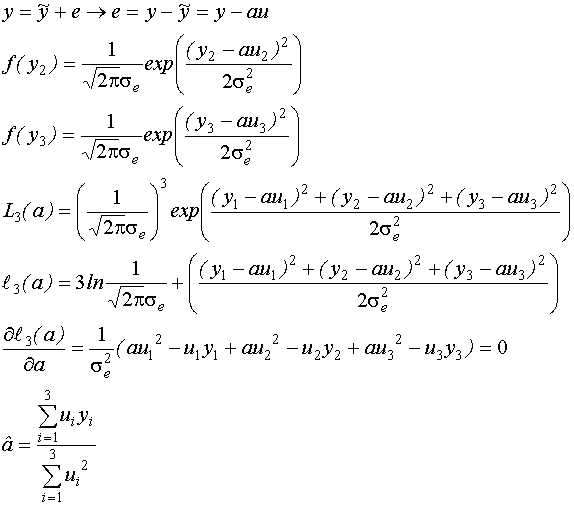
Полученная оценка 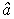совпадает с МНК оценкой при нормальном законе распределения. Недостатком метода максимального правдоподобия является необходимость знания закона распределения случайной величины e(t).

Тема 4. Статистический анализ уравнений регрессии

Цель и этапы статистического анализа уравнений регрессии

Проверка значимости

Проверка адекватности

Расчет доверительных интервалов

Цель и этапы статистического анализа уравнений регрессии

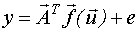
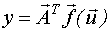-уравнение регрессии

Статистический анализ уравнения регрессии включает в себя три этапа:

I- проверка значимости оценок неизвестных коэффициентов модели.

II- проверка адекватности представления результатов эксперимента полученным у авнениям регрессии.

III- расчет доверительных интервалов для истинных значений входов.

Целью статистического анализа является уточнение структуры модели с обоснованием правильности ее выбора и оценка точности предсказания по модели.

Проверка значимости.

Имеем 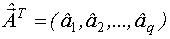- оценки соответствующих коэффициентов.

Мы должны проверить (оценить) коэффициенты 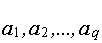на их отличие от нуля.

Проверка значимости i-ого коэффициента модели эквивалентна проверке гипотезы о том, что 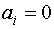(нуль-гипотеза). Исходными данными этой гипотезы являются оценка коэффициентов и дисперсия (точность) оценки. Проверка гипотезы сводится к использованию статистики с известным законом распределения.

Статистикой называют некоторое выражение, построенное на известных оценочных характеристиках.

Известно, что отношение модуля оценки к корню квадратному из оценки дисперсии называется t-распределением (Стьюдента).

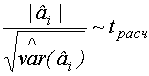
Нуль-гипотеза принимается, если отношение 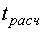меньше некоторого критического значения 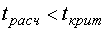. Если неравенство не выполняется, то нуль-гипотеза отвергается.

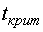- это квантиль распределения Стьюдента, соответствующий уровню значимости 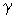и числу степеней свободы .

.

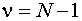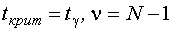Квантиль - это значение случайной величины, соответствующее заданной вероятности.

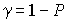, где Р- доверительная вероятность, то есть вероятность, с которой принимается нуль-гипотеза при выполнении нашего неравенства 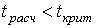. Обычно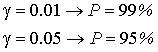

Квантили определяются по справочнику следующим образом:

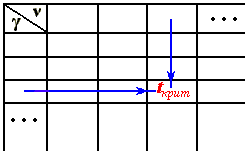
После проверки значимости все незначащие коэффициенты исключаются из модели. Таким образом осуществляется корректировка структуры модели.

Проверка адекватности.

Проверка адекватности сводится к проверке гипотезы о равенстве дисперсии адекватности и дисперсии внешнего шума: .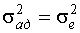

Дисперсия адекватности характеризует точность предсказания выхода по модели, то есть это дисперсия случайной величины, которая является разностью между экспериментальным значением выхода и значением выхода, рассчитанным по модели.

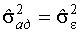
1. 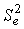-оценка дисперсии внешнего шума.

2.

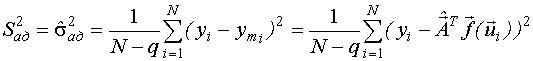
Отношение 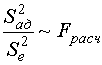- F-распределение (по закону Фишера)

Если выполняется неравенство 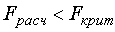, то модель признается адекватной экспериментальным данным. В противном случае, модель не адекватна, то есть структура модели выбрана неверно. Ее необходимо изменить и для новой структуры провести все исследование.

Квантиль ( 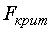) должен удовлетворять трем условиям ,

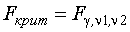где 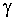-уровень значимости;

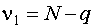- число степеней свободы числителя дисперсионного отношения;

- число степеней свободы знаменателя дисперсионного отношения.

Для определения 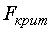используется справочник, но предварительно выбирается конкретное значение .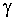